はじめに
前回は、並列システムの性能指標について紹介し、また、データ処理におけるアルゴリズムと、選択処理の並列化方法を紹介しました。今回からは、結合処理の並列化方法について説明します。まずは、結合処理における基本的な並列化方法について述べ、次に、ソートマージ結合の具体的な並列アルゴリズムを説明していきます。
結合処理の並列化方法
結合処理は、前回述べたとおり、複数のデータを、当該データを構成するレコード(タプル)における属性値を用いてある条件に基づいて連結することにより、1つのデータにする処理です。簡単のため、以降では、「 ある条件」は複数のデータの属性値が同一である、とします。すなわち、結合における最も一般的な方法である等結合を対象として話を進めていきます。また、特に断りがない限り、2つのデータを結合するものとします。
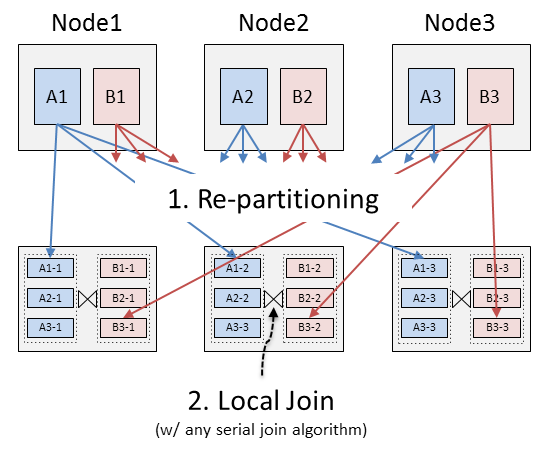
等結合処理における並列化の基本的な方法は、次の2つのステップからなります(図1 ) 。
データごとに、結合に用いる属性値(結合キー)を用いて、前述の分割方法(第5回 )により、レコードを複数の計算機に分配し
各計算機において、通常の単一計算機内での結合アルゴリズム(serial join algorithm)を用いて結合処理を行う
図1 等結合処理における並列化の基本的な方法1.により結合キーが同一のレコードは同じ計算機に分配されるので、2.においては、分配されたレコードを用いて単一計算機上で用いられる通常の結合処理を行えば良いというわけです。このような結合処理の並列化方法は分割結合(Partitioned Join) と呼ばれます。また、1.の処理は再分割処理(Re-partitioning、※1 ) 、2.の処理はローカル結合処理(Local Join)と呼ばれることが通例です。Hadoop MapReduceやその他の並列データ処理系においても、基本的にはこの方法で並列結合処理を実現しています。
なお、一方のデータをすべての計算機に複製できる場合は、再分割処理を行うことなく結合処理を行うことができます。このような方法はブロードキャスト結合(Broadcast Join、※2 )と呼ばれ、特に一方のデータ(A)が小さく、他方のデータ(B)が大きい場合に有効な方法であると考えられています。すなわち、Bのデータの再分割処理は、Aのデータを複数の計算機に複製する処理に比べて、処理量が大きいと考えられるため、Bのデータの再分割処理を省略することにより、全体としてより少ない処理量で当該結合を実行することができる可能性があります。当該方法は、Hiveやその他の並列データ処理系において用いられています。
ソートマージ結合における並列アルゴリズム
ソートマージ結合は、2つのデータにおいて同一の属性値を持つレコードを見つける方法として、データの整列(ソート)を用いるものです。すなわち、当該方法においては、双方のデータを整列し、それぞれの整列済みデータを先頭から順々に読み出すこと(マージ処理)により、一方のレコードの属性値と同一の値を持つ他方のレコードを見つけ出します。ソートマージ結合についてさらにくわしく知りたい方は、wikipedia などを参照してください。
ソートマージ結合の並列化は、前述の基本的な方法を適用して以下のように行うことができます。
並列ソートマージ結合1
各計算機のデータを読み出し、結合キーで分割(場合によっては、当該分割データをローカルに一時的に保存)
各計算機における当該分割データを各ノードに分配
各計算機でソートマージ結合を実行
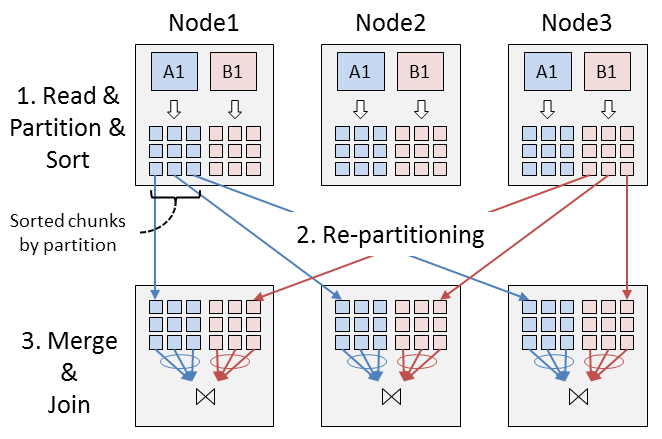
上記の方法は、前述の基本方法に忠実であり良いのですが、1.において、データをメモリ空間に読み出すため、その段階で当該データをある程度ソートしておくことにより、総計のI/O量を減らすことができる場合があります。よって、多くの場合、次のような改良方法が用いられます(図2 ) 。
並列ソートマージ結合2
各計算機のデータを読み出し、結合キーで分割しつつ、それぞれの分割データをメモリ空間上でキー順に整列(場合によっては、当該整列データをローカルに一時的に保存)
各計算機における整列済み当該分割データを各ノードに分配
各計算機で各々のデータにおいて(マルチウェイで)マージ処理を行い、各々の整列済みデータを用いて結合を行う
図2 並列ソートマージ結合いずれの結合方法においても、2.のデータの再分割では、たとえば結合キーに偏りがある場合においては、必ずしも結合処理を複数の計算機に均等に分割することは困難となり、すなわち、結合処理のスケーラビリティが低くなる可能性があります。このような問題を改善する1つの方法として、実際のデータの分布などに応じてデータを分配するなどの負荷分散処理を動的に行う手法が提案されています([2] ) 。
Hadoop MapReduceにおける結合処理
並列ソートマージ結合2を見ると、その処理の流れは、Hadoop MapReduceの処理の流れと非常に類似していることがわかります。すなわち、Hadoop MapReduceは一種のソートマージ結合処理フレームワークとして見ることができます。
Hadoop MapReduceの大枠としては、map、sort、shuffle、merge、reduceというフェーズがあり、mapにおいて読み出したデータをmapの出力キーにより整列(sort)し、当該キーにより計算機に再分割(shuffle)し、各計算機において分割データを併合(merge)し、その結果をreduceで読み出します。当該フレームワークにおいては、sort、shuffle、mergeの処理はあらかじめフレームワークにより規定されているため、ユーザー(アプリケーションプログラマ)がmapとreduceの動作を記述することにより、たとえば任意のキーによりソートマージ結合を行うことができます。すなわち、並列ソートマージ結合2の1.のフェーズをmapとその後のsortで行わせ、2.のフェーズをshuffleフェーズで行わせ、3のフェーズをmergeとその後のreduceで行わせることにより、結合を実現することができます。
なお、Hadoop MapReduceにおいては、アプリケーションプログラム(mapおよびreduce)は複数の入力を判別することはできないため、複数のデータを入力する際は、アプリケーションプログラム内で、それらを判別する必要があります。すなわち、実際に結合を行うreduce側で複数のデータを識別するために、mapで各データを(データに対する事前知識を基に)判別し、mapの出力レコードにタグを付けておく必要があります。この際、shuffleフェーズにおいては、タグを除いたmapの出力キーに基づいて、出力レコードを分配するように分割関数を定義しておきます。具体的には、Hadoop関連の書籍などを参照してください。
Hadoop MapReduceにおける整列処理
Hadoop MapReduceのフレームワーク自体は、上述したように、特に結合に特化した処理を行っているわけではないので、むしろ、一種の整列処理フレームワークであると見るほうが正しいかもしれません。
整列処理フレームワークとしてのHadoop MapReduceは、整列処理アプリケーションであるTeraSortが業界標準のソートベンチマークの1つであるGraySort において1位(ワールドレコード)を記録したことからもわかるように[3] 、非常にスケーラブルであることが実証されています。
TeraSortにおいては、Jobの起動時(Map処理が動作する前)に、事前にデータの一部をスキャンし、整列したい属性の統計情報を取得し、当該統計情報を用いて、Shuffleの際のキーの分割範囲を決定します。すなわち、TeraSortのshuffleにおいては、Hadoop MapReduceのデフォルトの分割方法であるハッシュ分割を用いずに、範囲分割を用います。各Reducerにおいては、それぞれの範囲のレコードを併合して、整列済みのデータをHDFSに書き出します。GraySortのルール的には、複数の計算機のデータを物理的に1つにする必要はなく、整列済みの部分データに順番を付けることができればOKであるとしているので、各ReducerがデータをHDFSに書き出したら、そこで処理は終了です。このように、データの実際に範囲に基づいて、動的に分割範囲を決定することにより、各計算機での処理量をなるべく均等になるようして、高いスケーラビリティを実現していることが見てとれます。
おわりに
今回は、結合処理の並列化における基本戦略について説明し、ソートマージ結合における具体的な並列アルゴリズムを説明しました。次回は、ハッシュ結合などにおける具体的な並列アルゴリズムを説明する予定です。