はじめに
前回 は、これまで説明してきたアルゴリズムの性能を定量的に見積り、比較しました。今回は、これらの性能見積りを用いて行うデータ処理(問い合わせ)の最適化方法について説明します。
データ処理(問い合わせ)の最適化
第4回で述べたように、HadoopのSQL処理系であるHiveをはじめとし、ImpalaやPrestoなどの宣言型言語を用いるデータ処理系においては、利用者は何を(What)処理してほしいかを処理系に指示するのみであり、どのように(How)処理をしてほしいかは指定しません。すなわち、当該処理系においては、どのように処理をするかは処理系自体が決める必要があり、与えられた問い合わせ(クエリ)を最も良いと思われる方法で処理します。このように、問い合わせにおいて最良と思われるデータ処理の方法を見つけることを「( 問い合わせ)最適化」と呼びます。
最適化においては、問い合わせを実行する前に、データ処理の性能見積りなどを行い、最も適切なデータ処理の方法を選択します[1] 。すなわち、ある問い合わせが与えられたときに、当該データ処理を遂行するすべて実行プランの性能見積りの結果を考慮し、最も高い性能が実現できると想定される実行プランを選びます。
たとえば、具体的には、次のようなことを考慮して、最適な実行プランを導出します。
選択(Selection) 、結合(Join) 、集約(Aggregation)でそれぞれどのようなアルゴリズムを用いるか
複数のデータがあるときに、それらをどのような順番で結合するか
実行プラン(Left-Deep、Right-Deepなど)の形はどうするか
特に並列データ処理においては、どのような戦略(Partitioned Join or Broadcast Join)でジョインを行うか
問い合わせ最適化方式は、System-Rと称される初期の関係データベースシステムにおいて研究・開発が始められました。System-Rにおける当該方式は、System-R最適化方式または当該方式の開発者であるSelingerさんの名前を用いてSelingerアルゴリズムと称され、現在のさまざまな関係データベースシステムおよびデータ処理系における最適化方式のベースとなっています。次項では、当該方式についてもう少しくわしく説明します。
System-R最適化方式(Selingerアルゴリズム)
System-R最適化方式は、おもに次に示す処理を行い、最適な実行プランを導出します。
実行プランの列挙
Left-Deep木における実行プランの列挙
最適な実行プランの選択
各実行プランのコストを算出し、最もコストが低い実行プランを選択[2]
それぞれをくわしく見ていきましょう。
実行プランの列挙
System-R最適化方式の実行プランの列挙においては、探索空間を絞るべく、木の形態をLeft-Deepに限定します。すなわち、実行プランの形態としては、Left-Deep木やRight-Deep木をはじめとし、さまざまなものが存在するものの、すべて形を対象としてしまうと、探索すべき空間が大きくなりすぎてしまい、現実的な時間で最適な実行プランを見つけることが困難となる可能性があるため、考慮すべき実行プランの数を実行プランの形を限定することにより削減します。
次に、Left-Deep木を対象に、実行プランを列挙します。最も単純な方法としては、考えられるすべての実行プランを列挙するものです。たとえば、R1、R2、R3、R4の4つのデータ(表)があるときに、これらのデータを結合する実行プラン(結合順序)は、4 P4 =4!=4×3×2×1=24通りあります。
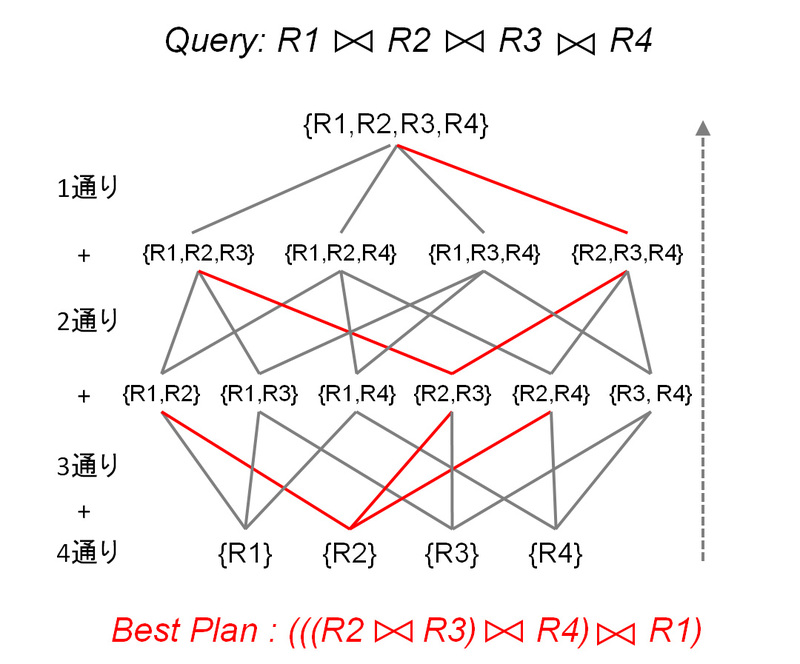
このようなナイーブな方法では、データの数が大きくなると比較すべき実行プランの数が増えすぎてしまう可能性があるため、System-R最適化方式では、実行プランの導出においては、k個のデータに対する最適な実行プランは、k-1個のデータに対する最適な実行プランを基に導出することができる、という最適性の原理が保証される性質を利用し、動的計画法を用いることにより、列挙する実行プランの数を削減します。たとえば上述の例では、4+3+2+1=10通りの実行プランを考慮すれば良いこととなります(図1 ) 。
図1 動的計画法による実行プランの列挙図1の例においては、まず、R1、R2、R3、R4のアクセスにおいて、最適な(最小のコストを持つ)実行サブプランR2を選択し、次に、R2と結合する最適な実行サブプランR2 R2 最後に、R2
整理すると、k個のデータを結合する実行プランを列挙する具体的なアルゴリズムは次に示すとおりです。
1.1つのデータをアクセスする最適な実行サブプランを見つける。
2.2つのデータを結合する最適な実行サブプランを見つける。このとき、ステップ1.で見つけた最適な実行サブプランの結果を木の左側(外表)とし、その他のデータを木の右側(内表)とする。
…
k. k個のデータを結合する最適な実行プランを見つける。このとき、ステップ(k-1)で見つけた最適な実行サブプランの結果を木の左側(外表)とし、残りの1つのデータを木の右側(内表)とする。
ただし、実際には、タプルの並び順(interesting orders)ごとに最適な実行サブプランを保持しておく必要があるため、考慮すべき組み合わせの数はもう少し増える可能性があります。すなわち、実行サブプランの段階では、次のステップでタプルの並び順を利用したアルゴリズムが適用される場合があるため、必ずしも最適な実行サブプランを1つに絞れない場合があります。
たとえば、ステップ(j)の出力データがステップ(j+1)の結合属性で整列されていない場合は、ステップ(j+1)における結合においては、一般的にはハッシュ結合のほうがソートマージ結合よりも有利ですが、ステップ(j)の出力データがステップ(j+1)の結合属性で整列されている場合は、ソートマージ結合がハッシュ結合よりも有利になる可能性があります。それにより、全体の実行プランも影響を受けることがあり、たとえば、ステップ(j)の結合において、ステップ(j+1)の結合属性で整列されたデータを出力するようなアルゴリズムを選択するほうが最適になる可能性があります。
このように、System-R最適化方式では、実行プランを列挙しつつ、最適な実行(サブ)プランを見つけていきます。さらにくわしく知りたい方は、参考文献[1][ 2] をご参照ください。
最適な実行プランの選択
当該方式においては、実行プランごとに実行時間に比例するようなコストを見積り、実行プランの性能比較を行います。このとき、問い合わせがアクセスするデータのサイズやレコードの数を見積るために、データの統計情報を用います。
データの統計情報には、たとえば、データ(表)のサイズ、データにおけるレコード(タプル)数、レコードにおける属性値ごとの統計情報(最大値、最小値、分布、カーディナリティ(濃度) 、ヒストグラムなど)などからなり、データのロードの際、もしくは、問い合わせの前に事前に保持しているものとします。
当該方式では、このような統計情報を用いることにより、与えられた問い合わせと実際にデータの性質において、アルゴリズムの優越を判別します。たとえば、
SELECT * FROM data WHERE data.attr = 1;
のような選択処理(Selection)においては、前回に述べたように、データの多くのレコードにアクセスする必要があるならばスキャンを選択し、一部のレコードのみにアクセスするならば索引スキャンを選択することが望ましいですが、属性data.attrが1000個の値があり、それぞれの値がほぼ一様分布で存在している場合は、data.attr = 1となる確率は0.1%(=1/1000)であると推定できるため、この場合においては、おそらく、索引スキャンを用いるほうが良いと判断できます。
並列データ処理系における最適化方式
昨今のHadoopやそれに類する並列データ処理系において、どのような最適化が行われているかを見てみましょう。
Hiveにおいては、Hive 0.14からSystem-R最適化方式と類似の方式を実装しており([3] ) 、また、Imapalaにおいても、Right-Deep木に限定して、System-R最適化方式と類似のものを実装しています([4]
PrestoやSpark SQLにおいては、上述のようなコストベースの最適化は行わず、おもに関係代数の等価変換やルールベースの最適化を行っている模様です。
HiveやImpalaにおいてはSystem-R最適化方式を採用しているものの、当該方式は、単一計算機(もしくは単一データパーティション)に対する方式であり、本来、そのままでは並列計算機(もしくは複数パーティション)に適用することはできません。すなわち、得られる実行プランは必ずしも最適解とはなりません。
IBMのDB2の並列版においては、"interesting partitions"というパーティションごとに最適な実行サブプランを保持する方法を用いることにより、System-R最適化方式を並列構成に適用しています([5] ) 。
おわりに
今回は、問い合わせの最適化について説明しました。次回は、Hadoopなどのデータ処理系における耐障害性のための仕組みについて説明します。
 R3を選択します。さらに、
R3を選択します。さらに、 R3と結合する最適な実行サブプランR2
R3と結合する最適な実行サブプランR2  R3
R3  R4を選択し、
R4を選択し、 R3
R3  R4と結合する最適な実行プランR2
R4と結合する最適な実行プランR2  R3
R3  R4
R4  R1を導出します。
R1を導出します。

