技術評論社サイトのロゴ

Direct3D 12 ゲームグラフィックス実践ガイド

サポートページ

ダウンロード

本書で使用したサンプルファイルをダウンロードできます。

以下より圧縮ファイルをダウンロードしていただき、適宜解凍してご利用ください。

（2024年11月11日更新）

ダウンロード
サンプルファイル（2刷対応版）

お詫びと訂正（正誤表）

本書の以下の部分に誤りがありました。ここに訂正するとともに、ご迷惑をおかけしたことを深くお詫び申し上げます。

（2026年1月26日最終更新）

P.245　6行目からの本文

誤 また、立体角は平面角2つを用いて表すことも可能です。球の半径をr、天頂角をθ、方位角φとした場合、3次元空間上の任意の点は球面座標を使って次のように表せます。
正 また、立体角は平面角2つを用いて表すことも可能です。球の半径をr、仰角をθ、方位角φとした場合、3次元空間上の任意の点は球面座標を使って次のように表せます。

P.56　図7.2

誤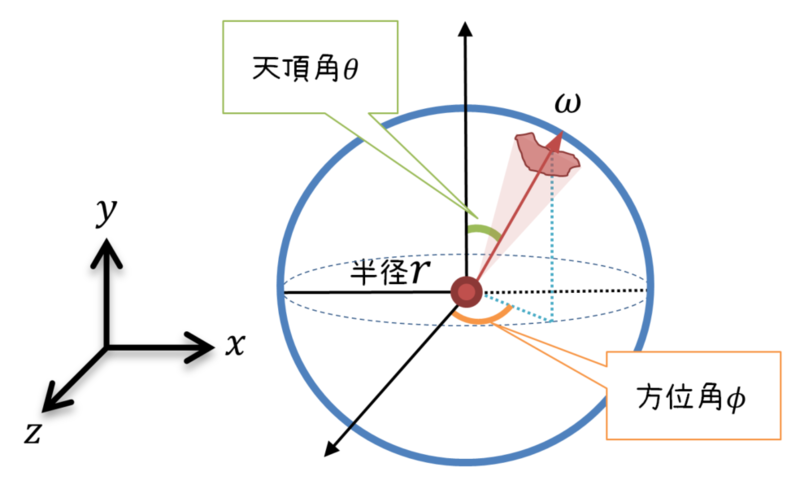
D3D2_245bef.png
正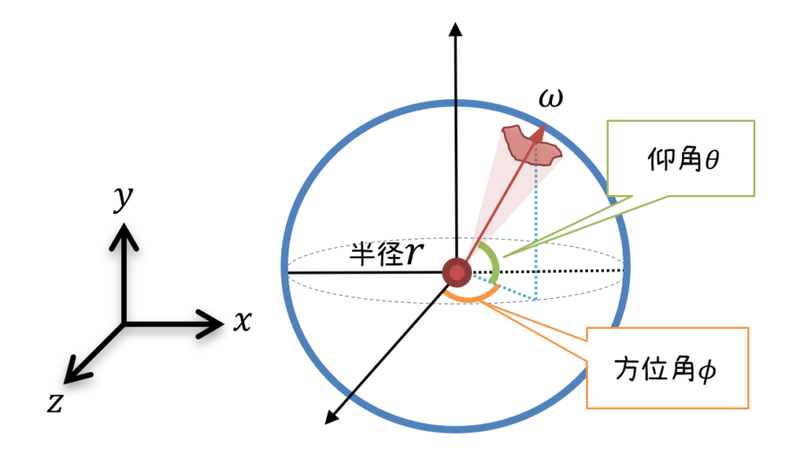
D3D2_245aft.png

P.245　図7.2からの本文

誤 円弧の長さは半径rと平面角の積で求められるので、方位角方向の弧の長さはrsinθdφで表されます。同様にして、天頂角方向の弧の長さを求めるとrdθとなります。
方位角方向と天頂方向の円弧によって形成される面積dAを考えると、次のようになります。
正 円弧の長さは半径rと平面角の積で求められるので、方位角方向の弧の長さはrsinθdφで表されます。同様にして、仰角方向の弧の長さを求めるとrdθとなります。
方位角方向と仰角方向の円弧によって形成される面積dAを考えると、次のようになります。

（以下2023年12月21日更新）

P.341　リスト10.16　370行

誤 
auto invW = 1.0f / float(w - 1);
auto invH = 1.0f / float(f - 1);
正 
auto invW = 1.0f / float(w);
auto invH = 1.0f / float(f);

サンプルプログラム　Chapter10　IESProfile.cpp　248行

誤 
auto idx = (w - 1) * y + x;
正 
auto idx = w * y + x;

（以下2021年12月23日更新）

P.245　ページ中央の式

誤 x = r sinθ cosθ
y = r cosθ
z = r sinθ sinθ
正 x = r sinθ cosΦ
y = r cosθ
z = r sinθ sinΦ

P.245　図7.2

誤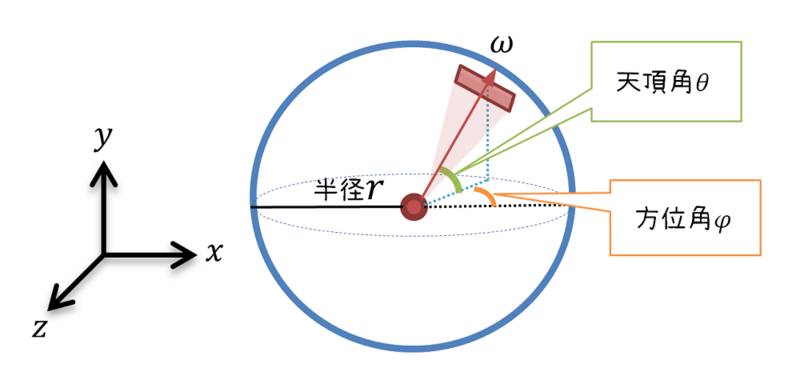
誤
正
正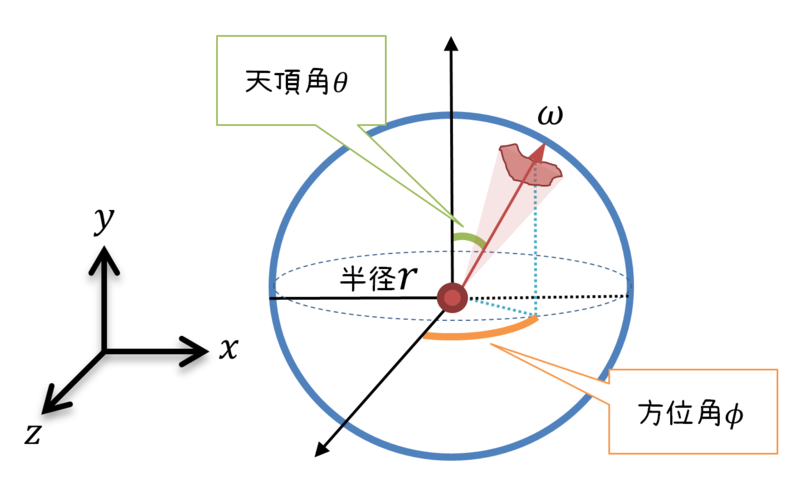