数学の未解決問題の1つとして知られているリーマン予想。つい最近では同じく未解決問題であるabc予想が話題になりました。それは不等式に関する予想ですが、
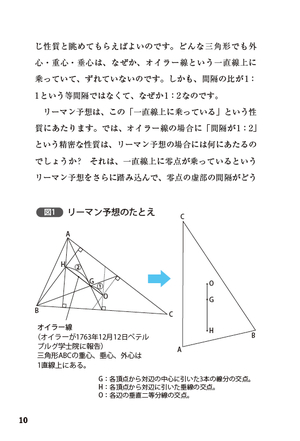
リーマン予想のこれまで、今そしてこれから
リーマン予想の感じをつかんでいただくために、
素数はイタリアのクロトーネにはじまったといわれています。
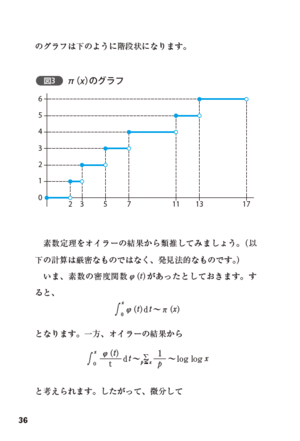
本書ではリーマン予想を一歩進めた深リーマン予想にも言及します。また、

2013.1.7
数学の未解決問題の1つとして知られているリーマン予想。つい最近では同じく未解決問題であるabc予想が話題になりました。それは不等式に関する予想ですが、

リーマン予想の感じをつかんでいただくために、
素数はイタリアのクロトーネにはじまったといわれています。

本書ではリーマン予想を一歩進めた深リーマン予想にも言及します。また、
