改めてアルゴリズムとは何か？

アルゴリズム（algorithm）の語源は、9世紀前半のイスラム世界の科学者であるアル＝フワーリズミーの名前に由来しています。アル＝フワーリズミーは、それまでに存在した計算の技法を、『⁠インドの数の計算法』という書籍にまとめたことで知られます。つまり、アルゴリズムは、数学的な考え方の基本と深く結びついています。

また、コンピュータの世界では、ある特定の目的を達成するための処理手順（プログラム）を指します。手法には「ソート（並べ替え⁠）⁠」⁠「⁠マージ（結合⁠）⁠」⁠「⁠分類」「⁠探索」などがあります。

プログラミングには必須か？

プログラマの方であれば、先述したアルゴリズム以外にもハッシュ法や暗号化手法、圧縮展開手法などを理解しておくことは、とても有用です。なぜなら、先人が残してくれた、間違いのない、効率的な手順なのですから。また、ITパスポート試験や基本情報処理技術者試験の出題項目に含まれています。

ただし、数学が苦手な方にとって、アルゴリズムを勉強しようとしても数式などで拒絶反応が出てしまう方が多いのではないでしょうか。

本書の特徴

本書は、既存のアルゴリズム解説書を小難しく感じる方のために「小学校の算数だけを基礎知識として、これから本格的にアルゴリズムを学ぶための基盤を作る」ことを目的に企画しました。

アルゴリズムの理解を妨げる要因

数学が苦手だという方は、実は小学校の算数の時点でモヤモヤした気持ちを感じています。本書では、最初に次の3点を例示しています。

• わかりやすいことは、必ずしも正しくない
• 小さな対象に適切な方法は、大きな対象にも適切とはかぎらない
• 正しさを決める要因はたくさんある

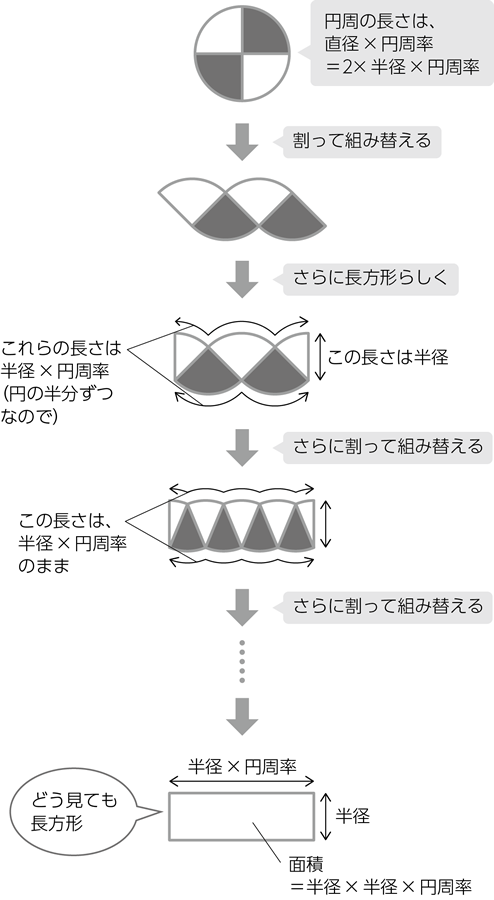
これらアルゴリズム的な価値観を、円の面積の導出法（図）などを挙げながら説明します。

円の面積の導出法アルゴリズムを理解する

第2章は「それは探しきれるか？―探索と探索アルゴリズム」です。探索法を説明する前に、なぜ探索が工夫されるのか、また、素直な探し方（逐次検索）ではダメなのか、に言及しているので、自分自身で具体的にイメージしながら読み進められます。

同様に、「⁠それは数えられるのか？―計算時間の見積もり」や「それはどういう規模か？―Order記法」と続きます。

また、第5 章「それは重要な問題か？―ドメインごとの優先事項⁠」⁠、第6章「それは解かなくてはならない問題なのか？―割り切りの方法」ではアルゴリズムを役立てる考え方を解説しています。

アルゴリズム解説書の読み方

最後に、本書で得た知識を活かして、アルゴリズムに関して定評のある書籍3冊を実際に読み解いています。初級編は『プログラマの数学』（⁠結城浩 著⁠）⁠、中級編は『アルゴリズムクイックリファレンス』（⁠G.T. Heinemanほか著、黒川利昭訳⁠）⁠、上級編は『The Art of ComputerProgramming』（⁠D.E. Knuth 著、有澤誠 訳）です。

本書はこれらを理解し、活用する糸口を得ることができるでしょう。