「ITエンジニアと数学」ー⁠ー みなさんはどんなイメージをお持ちでしょうか？ ITエンジニアと一言でいっても、職種はさまざまですので、業務の内容によってイメージは異なるかもしれません。数学を駆使してさまざまなアルゴリズムを使いこなすプログラマー、あるいは、統計学と機械学習でデータを分析するデータサイエンティストといったあたりでしょうか。ITの基礎となるデジタル計算機（あえてこう呼びます！）やプログラミング言語が、数学に基づいた原理に支えられているのは間違いありません。しかしながら、IT業界の中でも、「⁠まだまだ数学はよくわからない」「⁠これからでも数学の勉強を始めたい」と考える方は少なくないようです。

「機械学習に数学は必要？」問題

数年前、機械学習ブームが広がり始めたころ、「⁠機械学習をマスターするのに数学は必要か？」という話題が私のまわりで盛り上がりました。世間の声に耳を傾けると、「⁠機械学習を使いたければライブラリをインポートすればいいだけ。数学なんか知らなくてもいい」という過激な意見もあれば、「⁠え？ 数学を勉強していないITエンジニアなんているの？」という、これまた反応に困ってしまうコメントをいただくこともありました。いずれにしても、「⁠ITエンジニアが数学をどう学ぶべきか」は、みなさんの関心を集めるテーマのようで、Software Design誌でも数学をテーマにした特集がなんどか組まれてきました。

私自身の経験を振り返ると、ITよりも先に、数学に興味を持って深く勉強する機会がありました。当時は、数学と同時に物理学にも興味があり、「⁠物理学の計算をするための道具としての数学」と「数学の世界そのものの奥深さ」の両面に関心がありました。門外漢の方には、ピンとこない話かもしれませんが、物理学と数学はお互いに刺激を与えながら発展してきた歴史があります。数学者が新しい理論を作り出すと、その成果をもとに新しい物理学の理論が発展する ー⁠ー これは、なんとなく想像できる流れかもしれませんが、実はその逆もあります。物理学者が新しい着想を得たものの、それをうまく数式で表現できずに苦心するなかで、数学者がこれまで気づかなかった、まったく新しい数学の世界が発見されるということがあります。そのような歴史を知る中で、「⁠数学を道具として使うだけではなく、数学そのものをもっと深く理解したい！」という気持ちが生まれてきたのかもしれません。

理解を加速する「アクセラレーター」としての数学

さて、それでは、ITと数学にはどのような関係があるのでしょうか？ 冒頭で触れた機械学習に関して言うと、「⁠線形代数が機械学習の基礎です！」といった説明を耳にすることがあります。ところが・・・数式混じりの機械学習の教科書を開いてみると、線形代数の教科書に出てくるような「固有値、固有ベクトル、行列式」と言った言葉はあまり出てきません。もしくは、プログラミングのアルゴリズムを解説した書籍を開いてみましょう。アルゴリズムの実行時間を求める数式などは登場しますが、アルゴリズムの手続きそのものは、数式でもなんでもありません。疑似コードか、普通の言葉で処理の手続きが書かれていることがほとんどです。やはり、ライブラリをインポートして使うだけなら、数学の深い知識は要らないのでしょうか？ ー⁠ー いえいえ、そんなことはありません。

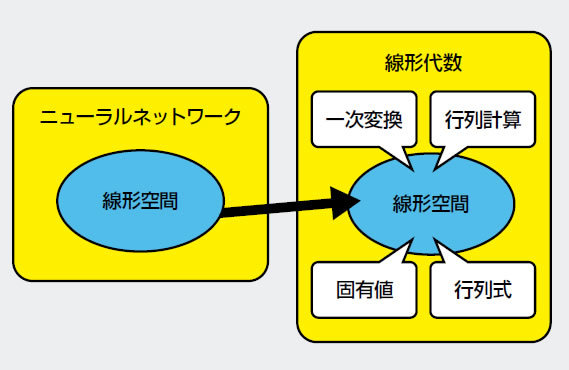
数学がもっとも得意とするのは、さまざまな例にあてはまる「共通の仕組み」を見つけ出すことです。図は、「⁠Software Design別冊：ITと数学」からの引用ですが、線形代数と言うのは、線形空間と呼ばれる数学的な「構造物」の性質を解き明かす学問であり、その性質を表すのが「固有値、固有ベクトル、行列式」と言った考え方です。一方、機械学習に登場する「ニューラルネットワーク（人間の脳を模した数理モデル⁠）⁠」の中には、線形空間と同じ構造が隠されています。「⁠線形空間の性質」をあらかじめ知っていれば、その知識を用いて、ニューラルネットワークの仕組みや性質が想像できるようになります。線形代数の知識をつかわずにニューラルネットワークの仕組みを学ぶよりは、圧倒的に理解のスピードが上がります。そして、同じ線形空間の構造は、図形変換、あるいは、Web検索のページランクなど、プログラミングの世界にも隠されています。つまり、数学の知識は、ITのさまざまな分野の理解をスピードアップする、「⁠ひと粒で二度も三度も美味しい」アクセラレーターなのです。

はじめの一歩を踏み出すヒント

逆の見方をすると、プログラミングの世界にも、数学を理解するためのヒントが隠されています。プログラミングで何か複雑な処理をしたい時に、きっちりと頭の上で理屈を考えてからコードを書きはじめる場合と、とにかくまずはコードを書いて、実際に動かしながら期待通りの処理ができるように修正していく場合があります。どちらがよいかは、ケースバイケースですが、数学の勉強にも似たような側面があります。数学の教科書といえば、まずは理屈をしっかりと説明して、具体例はその後で少しだけ・・・というパターンが多いものですが、人によっては、たくさんの具体例をじっくりと調べ上げることで理解が深まることもあるでしょう。Pythonなどのデータ分析が得意なプログラミング言語を活用すれば、数値計算やグラフの描画などで、数学の具体例を楽しむこともできます。

「Software Design別冊：ITと数学」には、機械学習を題材にした「線形代数」と「微積分」の入門、そして、プログラミングと数学の関係など、ITの世界に隠された数学、そしてまた、ITを活用して数学を学ぶためのヒントを紹介した記事が集められています。ITも数学も「はじめの一歩」が難しいものです。この書籍を活用して、ぜひ、はじめの一歩を踏み出すヒントを見つけだしてください。