第10回　マウスポインタに応じてカメラを水平および垂直に動かす

前回の第9回「マウスイベントを扱う」では、3次元空間に置いた立方体のオブジェクトにマウスのロールオーバー／ロールアウト、クリックへのインタラクションを加えた。今回は、これらのオブジェクトを回り込んで捉えるカメラの位置も、マウスポインタの動きに応じて変えてみたい。

マウスポインタの水平の位置に応じてカメラを回り込ませる

まず、オブジェクトの周囲を回るカメラの水平の動きだ。画面の中心から見たマウスポインタの水平位置に応じて、回り込む向きと速さを変えてみよう。第9回コード2「ロールオーバーしたオブジェクトの大きさが変わる」につぎのような手を加える。

var centerX = stageWidth / 2;
var centerY = stageHeight / 2;
var lastX = centerX;

function initialize() {

  document.onmousemove = recordMouse;

}

function recordMouse(eventObject) {
  lastX = eventObject.clientX;

}

function rotate(timeStamp) {

  // angle += timeStamp / 2000;
  angle += (lastX - centerX) / 5000;

}

画面の中心座標は変数（centerXとcenterY）に納めておく（垂直座標も後ほど使うので変数を設けておいた⁠）⁠。そして、マウスポインタが動いたときのonmousemoveイベントハンドラを定めた。コールバック関数（recordMouse()）は、イベントオブジェクト（eventObject）のMouseEvent.clientXプロパティから得たマウスポインタの水平座標を変数（lastX）に記録している。カメラを回り込ませる関数（rotate()）は、マウスポインタと画面の中心の水平座標の差に応じて回す角度（angle）を変えることにした。

これで、マウスポインタの水平位置に応じて、回り込むカメラの向きと速さが変わる。しかし、これだけでは、カメラの動きが少し気になる。onmousemoveハンドラは、Away3DのViewオブジェクトに定めた領域の外でもイベントを拾う。そして、ポインタの位置を遠ざけるほど、カメラがぐるぐると速く回ってしまう（図1⁠）⁠。

Viewオブジェクトの領域を超えても、カメラの速さはそれ以上増さないようにしたい。そこで、つぎのようにコールバック関数（recordMouse()）で、マウスポインタの水平座標がViewオブジェクトに定めた幅（stageWidth）を超えたら、座標値はその幅止まりとして扱うようにした。

function recordMouse(eventObject) {
  // lastX = eventObject.clientX;
  var mouseX = eventObject.clientX;
  if (mouseX < stageWidth) {
    lastX = mouseX;
  } else {
    lastX = stageWidth;
  }
}

これで、3次元領域の中心からのマウスポインタの水平位置に応じて、立方体のオブジェクトを捉えるカメラの回り込む向きと速さが変わるようになった。第9回コード2を手直ししたのが、つぎのコード1だ。

コード1　マウスポインタの水平座標に応じてカメラが回り込む向きと速さを変える

var LoaderEvent = require("awayjs-core/lib/events/LoaderEvent");
var Vector3D = require("awayjs-core/lib/geom/Vector3D");
var Matrix3D = require("awayjs-core/lib/geom/Matrix3D");
var AssetLibrary = require("awayjs-core/lib/library/AssetLibrary");
var URLRequest = require("awayjs-core/lib/net/URLRequest");
var RequestAnimationFrame = require("awayjs-core/lib/utils/RequestAnimationFrame");
var View = require("awayjs-display/lib/containers/View");
var DirectionalLight = require("awayjs-display/lib/entities/DirectionalLight");
var MouseEvent = require("awayjs-display/lib/events/MouseEvent");  //
var StaticLightPicker = require("awayjs-display/lib/materials/lightpickers/StaticLightPicker");
var PrimitiveCubePrefab = require("awayjs-display/lib/prefabs/PrimitiveCubePrefab");
var DefaultRenderer = require("awayjs-renderergl/lib/DefaultRenderer");
var TriangleMethodMaterial = require("awayjs-methodmaterials/lib/TriangleMethodMaterial");
var view;
var cube;
var imageDiffuse = "assets/trinket_diffuse.jpg";
var timer;
var ORIGIN = new Vector3D();
var angle = -Math.PI / 2;
var distance = 1500;
var stageWidth = 240;
var stageHeight = 180;
var centerX = stageWidth / 2;
var centerY = stageHeight / 2;
var lastX = centerX;
var lastY = centerY;
var urls = [
  "http://gihyo.jp/design/serial/01/away3d-typescript",
  "http://gihyo.jp/design/serial/01/createjs",
  "http://typescript.away3d.com",
  "https://developer.mozilla.org/ja/docs/Web/JavaScript",
  "http://createjs.com/#!/Home"
];
function initialize() {
  var directionalLight = createDirectionalLight(0.5, 0xFFFFFF);
  view = createView(stageWidth, stageHeight, 0x0);
  cube = createCube(400, 400, 400, directionalLight);
  setCamera(view.camera, distance, angle);
  cube.url = "http://fumiononaka.com";
  view.scene.addChild(cube);
  cloneMesh(cube, urls);
  AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
  AssetLibrary.load(new URLRequest(imageDiffuse));
  timer = new RequestAnimationFrame(rotate);
  timer.start();
  document.onmousemove = recordMouse;
  view.render();
}
function createView(width, height, backgroundColor) {
  var defaultRenderer = new DefaultRenderer();
  var view = new View(defaultRenderer);
  view.width = width;
  view.height = height;
  view.backgroundColor = backgroundColor;
  view.forceMouseMove = true;
  return view;
}
function createCube(width, height, depth, light) {
  var material = new TriangleMethodMaterial();
  var cube = new PrimitiveCubePrefab(width, height, depth, 1, 1, 1, false)
  .getNewObject();
  cube.material = material;
  setScale(cube, 1);
  setMouseListener(cube, onMouseOver, onMouseOut, onClick);
  material.lightPicker = new StaticLightPicker([light]);
  return cube;
}
function cloneMesh(mesh, urls) {
  var scene = view.scene;
  var count = urls.length;
  for (var i = 0; i < count; i++) {
    var clone = mesh.clone();
    var distance = getRandom(500, 1200);
    var scale = getRandom(0.3, 0.5);
    var rotationX = getRandom(-60, 60);
    var rotationY = getRandom(-180, 180);
    var position = getPolarPosition(distance, rotationX, rotationY);
    clone.x = position.x;
    clone.y = position.y;
    clone.z = position.z;
    clone.url = urls[i];
    setScale(clone, scale);
    clone.rotationY = rotationY;
    setMouseListener(clone, onMouseOver, onMouseOut, onClick);
    scene.addChild(clone);
  }
}
function setMouseListener(mesh, over, out, click) {
  mesh.addEventListener(MouseEvent.MOUSE_OVER, over);
  mesh.addEventListener(MouseEvent.MOUSE_OUT, out);
  mesh.addEventListener(MouseEvent.CLICK, click);
}
function recordMouse(eventObject) {
  var mouseX = eventObject.clientX;
  if (mouseX < stageWidth) {
    lastX = mouseX;
  } else {
    lastX = stageWidth;
  }
}
function onMouseOver(eventObject) {
  var mesh = eventObject.object;
  changeScale(mesh, 1.5);
}
function onMouseOut(eventObject) {
  var mesh = eventObject.object;
  changeScale(mesh, 1);
}
function onClick(eventObject) {
  var mesh = eventObject.object;
  window.open(mesh.url);
}
function setScale(mesh, scale) {
  mesh.scale = scale;
  changeScale(mesh, 1);
}
function changeScale(mesh, scale) {
  var _scale = mesh.scale * scale;
  mesh.transform.scale = new Vector3D(_scale, _scale, _scale);
}
function createDirectionalLight(ambient, color) {
  var light = new DirectionalLight();
  light.ambient = ambient;
  light.color = color;
  return light;
}
function onResourceComplete(eventObject) {
  var assets = eventObject.assets;
  var material = cube.material;
  material.texture = assets[0];
  view.render();
}
function rotate(timeStamp) {
  var camera = view.camera;
  angle += (lastX - centerX) / 5000;
  setCamera(camera, distance, angle);
  view.render();
}
function setCamera(camera, distance, angle) {
  camera.x = Math.cos(angle) * distance;
  camera.z = Math.sin(angle) * distance;
  camera.lookAt(ORIGIN);
}
function getRandom(min, max) {
  var random = Math.random() * (max - min) + min;
  return random;
}
function getPolarPosition(distance, rotationX, rotationY) {
  var vector = new Vector3D(distance, 0, 0);
  var matrix = new Matrix3D();
  matrix.appendRotation(rotationY, Vector3D.Y_AXIS);
  matrix.appendRotation(rotationX, Vector3D.X_AXIS);
  return matrix.transformVector(vector);
}

マウスポインタの垂直の位置に応じてカメラを上下する

つぎに、カメラに上下の動きも加えたい。やはり、画面の中心から見たマウスポインタの垂直位置に応じて動かす。onmousemoveイベントハンドラのコールバック関数（recordMouse()）で、つぎのようにイベントオブジェクト（eventObject）のMouseEvent.clientYプロパティから得たマウスポインタの垂直座標を変数（lastY）に記録した。なお、3次元の表示領域の高さ（stageHeight）を超えたら、座標値は増やさないことにしている。ここまでは、カメラを水平に回すのと同じ考え方だ。

var lastY = centerY;

function recordMouse(eventObject) {

  var mouseY = eventObject.clientY;

  if (mouseY < stageHeight) {
    lastY = mouseY;
  } else {
    lastY = stageHeight;
  }
}

function setCamera(camera, distance, angle) {
  var targetY = (lastY - centerY) * -10;

  camera.y += (targetY - camera.y) * 0.05;

}

カメラの垂直の動きは、水平と同じようにぐるぐる回しては、天地がひっくり返ってしまう。したがって、カメラを動かす関数（setCamera()）では、係数（-10）で幅をもたせて垂直座標を上下するようにした。これで、マウスポインタの水平の動きによる回転だけでなく、垂直座標に応じてカメラが上下するようになる（図2⁠）⁠。さて、このたびのお題はでき上がりだ。スクリプトは以下のコード2にまとめた。併せて、サンプル1をjsdo.itに掲げてある。

コード2　マウスポインタの画面中央からの座標に応じてカメラを水平および垂直に動かす

var LoaderEvent = require("awayjs-core/lib/events/LoaderEvent");
var Vector3D = require("awayjs-core/lib/geom/Vector3D");
var Matrix3D = require("awayjs-core/lib/geom/Matrix3D");
var AssetLibrary = require("awayjs-core/lib/library/AssetLibrary");
var URLRequest = require("awayjs-core/lib/net/URLRequest");
var RequestAnimationFrame = require("awayjs-core/lib/utils/RequestAnimationFrame");
var View = require("awayjs-display/lib/containers/View");
var DirectionalLight = require("awayjs-display/lib/entities/DirectionalLight");
var MouseEvent = require("awayjs-display/lib/events/MouseEvent");  //
var StaticLightPicker = require("awayjs-display/lib/materials/lightpickers/StaticLightPicker");
var PrimitiveCubePrefab = require("awayjs-display/lib/prefabs/PrimitiveCubePrefab");
var DefaultRenderer = require("awayjs-renderergl/lib/DefaultRenderer");
var TriangleMethodMaterial = require("awayjs-methodmaterials/lib/TriangleMethodMaterial");
var view;
var cube;
var imageDiffuse = "assets/trinket_diffuse.jpg";
var timer;
var ORIGIN = new Vector3D();
var angle = -Math.PI / 2;
var distance = 1500;
var stageWidth = 240;
var stageHeight = 180;
var centerX = stageWidth / 2;
var centerY = stageHeight / 2;
var lastX = centerX;
var lastY = centerY;
var urls = [
  "http://gihyo.jp/design/serial/01/away3d-typescript",
  "http://gihyo.jp/design/serial/01/createjs",
  "http://typescript.away3d.com",
  "https://developer.mozilla.org/ja/docs/Web/JavaScript",
  "http://createjs.com/#!/Home"
];
function initialize() {
  var directionalLight = createDirectionalLight(0.5, 0xFFFFFF);
  view = createView(stageWidth, stageHeight, 0x0);
  cube = createCube(400, 400, 400, directionalLight);
  setCamera(view.camera, distance, angle);
  cube.url = "http://fumiononaka.com";
  view.scene.addChild(cube);
  cloneMesh(cube, urls);
  AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
  AssetLibrary.load(new URLRequest(imageDiffuse));
  timer = new RequestAnimationFrame(rotate);
  timer.start();
  document.onmousemove = recordMouse;
  view.render();
}
function createView(width, height, backgroundColor) {
  var defaultRenderer = new DefaultRenderer();
  var view = new View(defaultRenderer);
  view.width = width;
  view.height = height;
  view.backgroundColor = backgroundColor;
  view.forceMouseMove = true;
  return view;
}
function createCube(width, height, depth, light) {
  var material = new TriangleMethodMaterial();
  var cube = new PrimitiveCubePrefab(width, height, depth, 1, 1, 1, false)
  .getNewObject();
  cube.material = material;
  setScale(cube, 1);
  setMouseListener(cube, onMouseOver, onMouseOut, onClick);
  material.lightPicker = new StaticLightPicker([light]);
  return cube;
}
function cloneMesh(mesh, urls) {
  var scene = view.scene;
  var count = urls.length;
  for (var i = 0; i < count; i++) {
    var clone = mesh.clone();
    var distance = getRandom(500, 1200);
    var scale = getRandom(0.3, 0.5);
    var rotationX = getRandom(-60, 60);
    var rotationY = getRandom(-180, 180);
    var position = getPolarPosition(distance, rotationX, rotationY);
    clone.x = position.x;
    clone.y = position.y;
    clone.z = position.z;
    clone.url = urls[i];
    setScale(clone, scale);
    clone.rotationY = rotationY;
    setMouseListener(clone, onMouseOver, onMouseOut, onClick);
    scene.addChild(clone);
  }
}
function setMouseListener(mesh, over, out, click) {
  mesh.addEventListener(MouseEvent.MOUSE_OVER, over);
  mesh.addEventListener(MouseEvent.MOUSE_OUT, out);
  mesh.addEventListener(MouseEvent.CLICK, click);
}
function recordMouse(eventObject) {
  var mouseX = eventObject.clientX;
  var mouseY = eventObject.clientY;
  if (mouseX < stageWidth) {
    lastX = mouseX;
  } else {
    lastX = stageWidth;
  }
  if (mouseY < stageHeight) {
    lastY = mouseY;
  } else {
    lastY = stageHeight;
  }
}
function onMouseOver(eventObject) {
  var mesh = eventObject.object;
  changeScale(mesh, 1.5);
}
function onMouseOut(eventObject) {
  var mesh = eventObject.object;
  changeScale(mesh, 1);
}
function onClick(eventObject) {
  var mesh = eventObject.object;
  window.open(mesh.url);
}
function setScale(mesh, scale) {
  mesh.scale = scale;
  changeScale(mesh, 1);
}
function changeScale(mesh, scale) {
  var _scale = mesh.scale * scale;
  mesh.transform.scale = new Vector3D(_scale, _scale, _scale);
}
function createDirectionalLight(ambient, color) {
  var light = new DirectionalLight();
  light.ambient = ambient;
  light.color = color;
  return light;
}
function onResourceComplete(eventObject) {
  var assets = eventObject.assets;
  var material = cube.material;
  material.texture = assets[0];
  view.render();
}
function rotate(timeStamp) {
  var camera = view.camera;
  angle += (lastX - centerX) / 5000;
  setCamera(camera, distance, angle);
  view.render();
}
function setCamera(camera, distance, angle) {
  var targetY = (lastY - centerY) * -10;
  camera.x = Math.cos(angle) * distance;
  camera.z = Math.sin(angle) * distance;
  camera.y += (targetY - camera.y) * 0.05;
  camera.lookAt(ORIGIN);
}
function getRandom(min, max) {
  var random = Math.random() * (max - min) + min;
  return random;
}
function getPolarPosition(distance, rotationX, rotationY) {
  var vector = new Vector3D(distance, 0, 0);
  var matrix = new Matrix3D();
  matrix.appendRotation(rotationY, Vector3D.Y_AXIS);
  matrix.appendRotation(rotationX, Vector3D.X_AXIS);
  return matrix.transformVector(vector);
}

サンプル1　Away3D 14/11/05: Dealing with the mouse interactions for objects and the camera

減速を表す式ーイーズアウト

結びとして、オブジェクトを動かす式について、少し補っておこう。カメラを水平および垂直に動かすとき、その度合いはつぎのような式で定めた。すると、マウスポインタの動きがそのままカメラに伝わるのではなく、加速や減速が与えられる。

function rotate(timeStamp) {

  angle += (lastX - centerX) / 5000;

}
function setCamera(camera, distance, angle) {
  var targetY = (lastY - centerY) * -10;

  camera.y += (targetY - camera.y) * 0.05;

}

この式は、一般につぎのように表される。アニメーションは、目標の位置に近づくほど動きが遅くなる（図3⁠）⁠。目標値と現在値の差に速度を比例させているからだ。終わりに近づくにつれ減速する動きは「イーズアウト」と呼ばれる。インターフェイスなどでおなじみだろう。比例係数（減速率）には、0から1の間の数値を与える。

速度 = (目標値 - 現在値) * 減速率   (0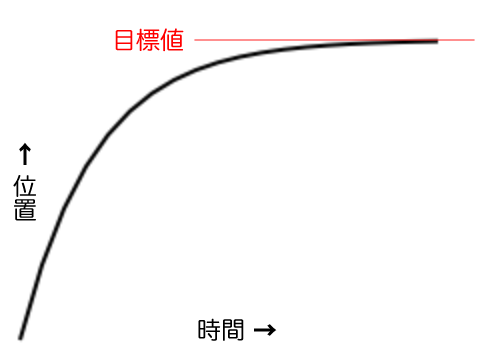

位置を速度に足し込んでつぎの位置を求めるというのは、数学の微分の考え方にもとづく。つまり、広く一般に使える。ただ、「⁠微分」と聞くと身構えてしまう人が多い。けれど、「⁠考え方」としては、位置の時間にもとづく変化が「速度」で、それを時々刻々「位置」に加えれば物体の運動が表せるということにすぎない。

この「考え方」を用いると、一見複雑そうな動きが簡単な四則演算で表せることも少なくない。「⁠イーズアウト」はそのひとつの例だ。また、連載「HTML5のCanvasでつくるダイナミックな表現―CreateJSを使う」で解説したつぎのサンプル2は、バネのように弾みのついた動きを四則演算で導いている（⁠「⁠マウスポインタの軌跡を滑らかな線で描きながら消す」参照⁠）⁠。

サンプル2　EaselJS 0.8.0: Smooth Line tuned

微分計算そのものはしなくても、その考え方を知るだけで、運動の式の扱いについて応用の幅が広がる。たとえば、Webに公開されたサンプルコードを開いて見たときも、読み解く力が備わるだろう。興味をもたれた読者は「速度から位置を決めるアニメーションー微分により運動を考える」をお読みいただきたい（15分間の講演録画も掲載⁠）⁠。

マウスポインタの水平の位置に応じてカメラを回り込ませる

マウスポインタの垂直の位置に応じてカメラを上下する

減速を表す式 ー イーズアウト

減速を表す式ーイーズアウト