第15回からこれまで、
立方体の頂点をワイヤーフレームで結ぶ
今回書くコードは、


第17回コード2では、
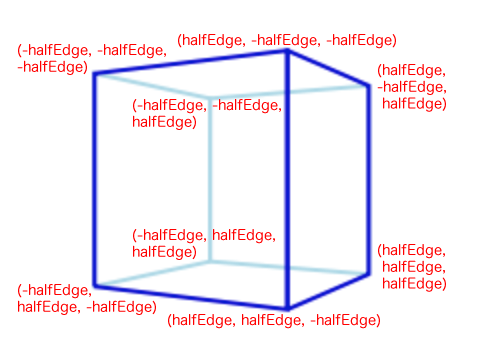
一辺の半分の長さから8頂点座標
var points;
var angle = 0; // Math.PI / 36;
function initialize() {
// points = createStarPoints(5, 65, 25);
points = createCubePoints(50);
}
/*
function createStarPoints(numVertices, longRadius, shortRadius) {
}
*/
function createCubePoints(halfEdge) {
var cubePoints = [
new Point3D(-halfEdge, -halfEdge, -halfEdge),
new Point3D(halfEdge, -halfEdge, -halfEdge),
new Point3D(halfEdge, halfEdge, -halfEdge),
new Point3D(-halfEdge, halfEdge, -halfEdge),
new Point3D(-halfEdge, -halfEdge, halfEdge),
new Point3D(halfEdge, -halfEdge, halfEdge),
new Point3D(halfEdge, halfEdge, halfEdge),
new Point3D(-halfEdge, halfEdge, halfEdge)
];
return cubePoints;
}この書替えだけで、
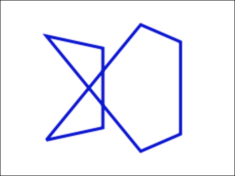
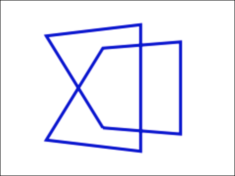
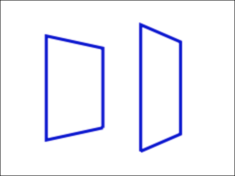
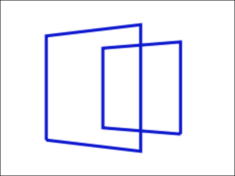
立方体の面を頂点番号で定める
立方体のそれぞれの面を、
そこで、
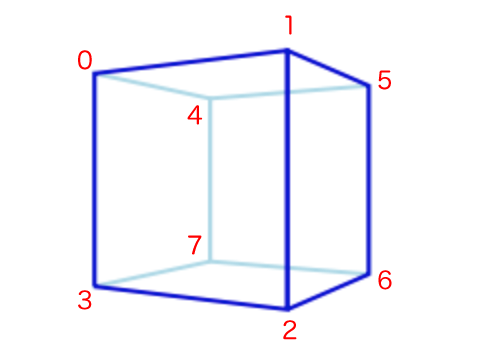
3次元座標
function Face(pos0, pos1, pos2, pos3) {
this.length = 4;
this[0] = pos0;
this[1] = pos1;
this[2] = pos2;
this[3] = pos3;
}この面のクラス
var points;
var facesVertices;
function initialize() {
points = createCubePoints(50);
facesVertices = getFacesVertices();
// draw(points);
drawFaces(points, facesVertices);
}
function getFacesVertices() {
var vertices = [
new Face(0, 1, 2, 3),
new Face(5, 4, 7, 6)
];
return vertices;
}面(Face)
新たにほしいのは、
このメソッドはできたとしよう。論文をあらすじから考えるのと同じで、
面(Face)
function rotate(eventObject) {
// draw(points2D);
drawFaces(points2D, facesVertices);
}
function drawFaces(points, faces) {
var numFaces = faces.length;
drawGraphics.clear();
for (var i = 0; i < numFaces; i++) {
var face = faces[i];
var facePoints = face.getFacePoints(points);
draw(facePoints);
}
stage.update();
}面のクラス
function draw(points) {
var count = points.length;
var point = points[count - 1];
drawGraphics // .clear()
.beginStroke("mediumblue")
.setStrokeStyle(3)
.moveTo(point.x, point.y);
for (var i = 0; i < count; i++) {
point = points[i];
drawGraphics.lineTo(point.x, point.y);
}
// stage.update();
}今回の課題で残るは、
Face.prototype.getFacePoints = function (points) {
var faces = this.length;
var facePoints = [];
for (var i = 0; i < faces; i++) {
facePoints[i] = points[this[i]];
}
return facePoints;
};これで、
function draw(points) {
drawGraphics
.beginStroke("mediumblue")
.setStrokeStyle(1)
.moveTo(point.x, point.y);
}
function getFacesVertices() {
var vertices = [
new Face(0, 1, 2, 3),
new Face(1, 5, 6, 2),
new Face(4, 0, 3, 7),
new Face(5, 4, 7, 6)
];
return vertices;
}読者の中には、
今回書上げたコード全体を以下にまとめよう。見やすさも考えて、
<script src="http://code.createjs.com/easeljs-0.7.1.min.js"></script>
<script>
// Point3D
function Point3D(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
}
Point3D.prototype.getProjetedPoint = function(focalLength) {
var point2D = new createjs.Point();
var w = focalLength / (focalLength + this.z);
point2D.x = this.x * w;
point2D.y = this.y * w;
return point2D;
};
// Face
function Face(pos0, pos1, pos2, pos3) {
this.length = 4;
this[0] = pos0;
this[1] = pos1;
this[2] = pos2;
this[3] = pos3;
}
Face.prototype.getFacePoints = function (points) {
var faces = this.length;
var facePoints = [];
for (var i = 0; i < faces; i++) {
facePoints[i] = points[this[i]];
}
return facePoints;
};
</script>立方体の4面をワイヤーフレームで描き、
<script>
var stage;
var drawGraphics;
var points;
var angle = 0;
var matrix = new createjs.Matrix2D();
var stageCenterX;
var _point = new createjs.Point();
var points2D = [];
var facesVertices;
var focalLength = 300;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageCenterX = canvasElement.width / 2;
drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);
points = createCubePoints(50);
facesVertices = getFacesVertices();
drawFaces(points, facesVertices);
createjs.Ticker.addEventListener("tick", rotate);
stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
var mouseX = eventObject.stageX;
angle = (mouseX - stageCenterX) * 1 / 300;
}
function rotate(eventObject) {
var count = points.length;
points2D.length = 0;
matrix.identity().rotate(angle);
for (var i = 0; i < count; i++) {
var point = points[i];
matrix.transformPoint(point.x, point.z, _point);
point.x = _point.x;
point.z = _point.y;
points2D[i] = point.getProjetedPoint(focalLength);
}
drawFaces(points2D, facesVertices);
}
function drawFaces(points, faces) {
var numFaces = faces.length;
drawGraphics.clear();
for (var i = 0; i < numFaces; i++) {
var face = faces[i];
var facePoints = face.getFacePoints(points);
draw(facePoints);
}
stage.update();
}
function draw(points) {
var count = points.length;
var point = points[count - 1];
drawGraphics
.beginStroke("mediumblue")
.setStrokeStyle(1)
.moveTo(point.x, point.y);
for (var i = 0; i < count; i++) {
point = points[i];
drawGraphics.lineTo(point.x, point.y);
}
}
function createGraphics(x, y) {
var drawShape = new createjs.Shape();
drawShape.x = x;
drawShape.y = y;
stage.addChild(drawShape);
return drawShape.graphics;
}
function createCubePoints(halfEdge) {
var cubePoints = [
new Point3D(-halfEdge, -halfEdge, -halfEdge),
new Point3D(halfEdge, -halfEdge, -halfEdge),
new Point3D(halfEdge, halfEdge, -halfEdge),
new Point3D(-halfEdge, halfEdge, -halfEdge),
new Point3D(-halfEdge, -halfEdge, halfEdge),
new Point3D(halfEdge, -halfEdge, halfEdge),
new Point3D(halfEdge, halfEdge, halfEdge),
new Point3D(-halfEdge, halfEdge, halfEdge)
];
return cubePoints;
}
function getFacesVertices() {
var vertices = [
new Face(0, 1, 2, 3),
new Face(1, 5, 6, 2),
new Face(4, 0, 3, 7),
new Face(5, 4, 7, 6)
];
return vertices;
}
</script>いつものとおり、



