第22回　立方体の6面をx軸とy軸で回す

前回の第21回「水平に回す立方体の面を塗る」では、立方体四方の面をy軸で水平に回した。今回は6面を揃えてx軸の回転も加える。つまり、マウスポインタの位置に応じて、立方体を水平および垂直に回してみよう。

立方体に上面と底面を加える

前回は、立方体の四方の面しか塗らなかった。y軸で水平に回すだけなので、どうせ上面と底面は見えないからだ。今回はx軸で垂直にも回すので、上面と底面も加える。それに、ふたつの面を加えないと立方体の中が見えてしまって、裏返った面は塗らないという手が使えなくなる。立方体の8頂点にはインデックスをふっておいた（第20回図3再掲⁠）⁠。

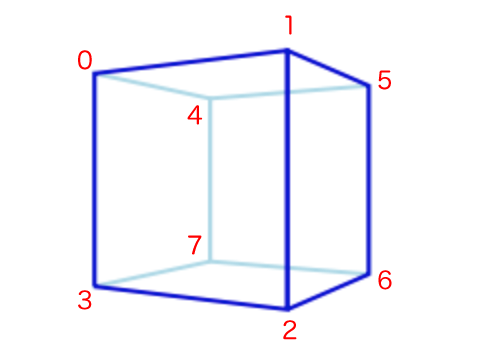
そして、面はクラス（Face）に4頂点インデックスを与えて定めた。ただし、面の裏表を調べるため、頂点の順序はふたつのベクトルの外積が右ネジの位置になるように、時計回りに決めなければならなかった（第21回図4再掲⁠）⁠。そこで、面のオブジェクトの配列をつくって返す関数（getFacesVertices()）に、以下のように上面と底面を加える。

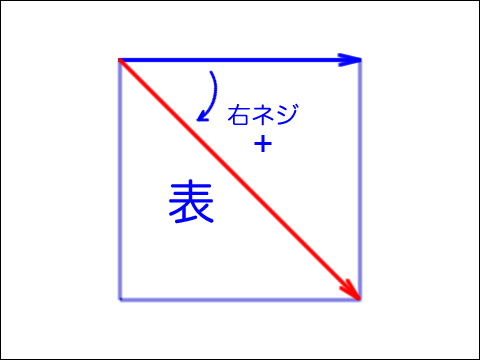
function getFacesVertices() {
  var vertices = [
    new Face(0, 1, 2, 3, getRandomColor()),
    new Face(1, 5, 6, 2, getRandomColor()),
    new Face(4, 0, 3, 7, getRandomColor()),
    new Face(4, 5, 1, 0, getRandomColor()),    // 上面
    new Face(6, 7, 3, 2, getRandomColor()),    // 底面
    new Face(5, 4, 7, 6, getRandomColor())
  ];
  return vertices;
}

x軸とy軸の回転を扱う準備

いきなりx軸で回す前に、xy両軸での回転が扱えるよう第21回コード2「水平に回す立方体の表向きの面だけを描く」に下ごしらえを施す。まだ、y軸で水平に回すという動きは変えない。まず、変数のもち方から取りかかろう。立方体の回転角はy軸にx軸周りが加わる。また、マウスポインタの位置を測る中心点もxy座標が要る。そこで、ふたつの変数（angleとstageCenter）は、以下のようにPointオブジェクトで与えることにした。それにともなって、変数との値のやり取りの仕方も変わってくる。

var angle = new createjs.Point();

// var stageCenterX;
var stageCenter = new createjs.Point();
function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  // stageCenterX = canvasElement.width / 2;
  stageCenter.x = canvasElement.width / 2;
  stageCenter.y = canvasElement.height / 2;
  // drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);
  drawGraphics = createGraphics(stageCenter.x, stageCenter.y);

  createjs.Ticker.addEventListener("tick", rotate);
  stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
  var mouseX = eventObject.stageX;
  // angle = (mouseX - stageCenterX) * 1 / 300;
  angle.y = (mouseX - stageCenter.x) / 300;
}
function rotate(eventObject) {

  // matrix.identity().rotate(angle);
  matrix.identity().rotate(angle.y);

}

前述のとおり、まだ動きはこれまでと変わらない。立方体はマウスポインタの水平位置に応じてy軸で回る（図1⁠）⁠。新たに加えた上面も底面も見えない。けれど、これでx軸周りの扱いが加えられるようになった。立方体を回転する処理は、以下のコード1のように変わった。なお、クラスの定めには手を触れていないので省いている。

コード1　マウスポインタの位置に応じて立方体をy軸で回す

var stage;
var drawGraphics;
var points;
var angle = new createjs.Point();
var matrix = new createjs.Matrix2D();
var stageCenter = new createjs.Point();
var _point = new createjs.Point();
var points2D = [];
var facesVertices;
var focalLength = 300;
function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  stageCenter.x = canvasElement.width / 2;
  stageCenter.y = canvasElement.height / 2;
  drawGraphics = createGraphics(stageCenter.x, stageCenter.y);
  points = createCubePoints(50);
  facesVertices = getFacesVertices();
  drawFaces(points, facesVertices);
  createjs.Ticker.addEventListener("tick", rotate);
  stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
  var mouseX = eventObject.stageX;
  angle.y = (mouseX - stageCenter.x) / 300;
}
function rotate(eventObject) {
  var count = points.length;
  points2D.length = 0;
  matrix.identity().rotate(angle.y);
  for (var i = 0; i < count; i++) {
    var point = points[i];
    matrix.transformPoint(point.x, point.z, _point);
    point.x = _point.x;
    point.z = _point.y;
    points2D[i] = point.getProjetedPoint(focalLength);
  }
  drawFaces(points2D, facesVertices);
}
function drawFaces(points, faces) {
  var numFaces = faces.length;
  drawGraphics.clear();
  for (var i = 0; i < numFaces; i++) {
    var face = faces[i];
    var facePoints = face.getFacePoints(points);
    if (isFront(facePoints)) {
      draw(facePoints, face.color);
    }
  }
  stage.update();
}
function isFront(facePoints) {
  var origin = facePoints[0];
  var point0 = MathUtils.subtractVectors(origin, facePoints[1]);
  var point1 = MathUtils.subtractVectors(origin, facePoints[2]);
  return (0 <= MathUtils.crossProduct2D(point0, point1));
}
function draw(points, color) {
  var count = points.length;
  var point = points[count - 1];
  drawGraphics
  .beginFill(color)
  .moveTo(point.x, point.y);
  for (var i = 0; i < count; i++) {
    point = points[i];
    drawGraphics.lineTo(point.x, point.y);
  }
}
function createGraphics(x, y) {
  var drawShape = new createjs.Shape();
  drawShape.x = x;
  drawShape.y = y;
  stage.addChild(drawShape);
  return drawShape.graphics;
}
function createCubePoints(halfEdge) {
  var cubePoints = [
    new Point3D(-halfEdge, -halfEdge, -halfEdge),
    new Point3D(halfEdge, -halfEdge, -halfEdge),
    new Point3D(halfEdge, halfEdge, -halfEdge),
    new Point3D(-halfEdge, halfEdge, -halfEdge),
    new Point3D(-halfEdge, -halfEdge, halfEdge),
    new Point3D(halfEdge, -halfEdge, halfEdge),
    new Point3D(halfEdge, halfEdge, halfEdge),
    new Point3D(-halfEdge, halfEdge, halfEdge)
  ];
  return cubePoints;
}
function getFacesVertices() {
  var vertices = [
    new Face(0, 1, 2, 3, getRandomColor()),
    new Face(1, 5, 6, 2, getRandomColor()),
    new Face(4, 0, 3, 7, getRandomColor()),
    new Face(4, 5, 1, 0, getRandomColor()),
    new Face(6, 7, 3, 2, getRandomColor()),
    new Face(5, 4, 7, 6, getRandomColor())
  ];
  return vertices;
}
function getRandomColor() {
  return createjs.Graphics.getRGB(Math.floor(MathUtils.getRandomInt(0, 0xFFFFFF)));
}

立方体をx軸でも回す

いよいよ、立方体の回転にx軸も加える。つまり、マウスポインタの位置に応じて、立方体が上下左右に回ることになる。さて、どうしたら3次元座標をx軸で回転できるか。実は、y軸で回すのと変わらない。2次元平面で座標を変換するMatrix2D.transformPoint()メソッドが使える。y軸で回転するときは、「⁠視点」を変えて真上から見たxz平面で座標変換した（第16回「3次元空間で座標を回す」の「z座標を加えてy軸で回す」の項参照⁠）⁠。今度は、真横から見てzy平面で回せばよい（図2⁠）⁠。

3次元空間座標をxy両軸で回すなら、クラス（Point3D）のメソッドとして備えた方が使いやすいだろう。引数には、つぎのようにMatrix2Dオブジェクトと回転軸を渡す。回転軸は"x"か"y"かの文字列で示す。

Point3DオブジェクトrotatePoint(Matrix2Dオブジェクト, 回転軸)

例によって、メソッドはできたものとして、それを呼び出すコードから以下のように書き替えよう。回転するMatrix2Dオブジェクトは、x軸とy軸のふたつを分けて変数（matrixXとmatrixY）に定める。回転角を決めるStage.stagemousemoveイベントのリスナー関数（setAngle()）は、マウスポインタのxy座標からy軸とx軸それぞれの回転角を変数（angle）のPointオブジェクトに与える。

立方体を回すTicker.tickイベントのリスナー関数（rotate()）は、y軸とx軸のMatrix2Dオブジェクト（matrixXとmatrixY）をそれぞれ定められた角度回転する。そして8頂点座標は、できたことにしたクラス（Point3D）のメソッド（rotatePoint()）にMatrix2Dオブジェクトと回転軸の引数を渡して回す。なお、クラスのメソッドで座標を変換するようにしたため、Matrix2D.transformPoint()メソッドで使い回すPointオブジェクトはクラスに定めることとし、変数（_point）からは除く。

// var matrix = new createjs.Matrix2D();
var matrixX = new createjs.Matrix2D();
var matrixY = new createjs.Matrix2D();

// var _point = new createjs.Point();

function setAngle(eventObject) {
  var mouseX = eventObject.stageX;
  var mouseY = eventObject.stageY;
  angle.y = (mouseX - stageCenter.x) / 300;
  angle.x = (mouseY - stageCenter.y) / -300;
}
function rotate(eventObject) {
  var count = points.length;
  points2D.length = 0;
  // matrix.identity().rotate(angle.y);
  matrixY.identity().rotate(angle.y);
  matrixX.identity().rotate(angle.x);
  for (var i = 0; i < count; i++) {
    var point = points[i];
    /*
    matrix.transformPoint(point.x, point.z, _point);
    point.x = _point.x;
    point.z = _point.y;
    */
    point.rotatePoint(matrixY, "y");
    point.rotatePoint(matrixX, "x");
    points2D[i] = point.getProjetedPoint(focalLength);
  }
  drawFaces(points2D, facesVertices);
}

改めて、クラス（Point3D）に座標回転のメソッド（rotatePoint()）を加えよう。ふたつの引数はもう決めた。また、「⁠視点」を変えることでMatrix2D.transformPoint()メソッドにより、y軸とx軸それぞれの回転ができるという考え方も確かめた。そこで、自身のプロパティである3次元座標を回転するメソッドはつぎのように定めた。

Point3D._point = new createjs.Point();
Point3D.prototype.rotatePoint = function(matrix, axis) {
  if (axis == "y") {
    matrix.transformPoint(this.x, this.z, Point3D._point);
    this.x = Point3D._point.x;
    this.z = Point3D._point.y;
  } else if (axis == "x") {
    matrix.transformPoint(this.z, this.y, Point3D._point);
    this.z = Point3D._point.x;
    this.y = Point3D._point.y;
  }

};

これらの手を加えれば、晴れて立方体がマウスポインタの位置に応じて、y軸およびx軸で上下左右に回るようになる（図3⁠）⁠。書上げたコードを以下にまとめよう。コード2は3つのクラスの定めだ。そして、これらのクラスを使ったインタラクティブな立方体のアニメーションがコード3のスクリプトである。

コード2　3次元座標と面および数学計算のクラス定義

// Point3D
function Point3D(x, y, z) {
  this.x = x;
  this.y = y;
  this.z = z;
}
Point3D._point = new createjs.Point();
Point3D.prototype.getProjetedPoint = function(focalLength) {
  var point2D = new createjs.Point();
  var w = focalLength / (focalLength + this.z);
  point2D.x = this.x * w;
  point2D.y = this.y * w;
  return point2D;
};
Point3D.prototype.rotatePoint = function(matrix, axis) {
  if (axis == "y") {
    matrix.transformPoint(this.x, this.z, Point3D._point);
    this.x = Point3D._point.x;
    this.z = Point3D._point.y;
  } else if (axis == "x") {
    matrix.transformPoint(this.z, this.y, Point3D._point);
    this.z = Point3D._point.x;
    this.y = Point3D._point.y;
  }
};
// Face
function Face(pos0, pos1, pos2, pos3, color) {
  this.length = 4;
  this.color = color;
  this[0] = pos0;
  this[1] = pos1;
  this[2] = pos2;
  this[3] = pos3;
}
Face.prototype.getFacePoints = function (points) {
  var faces = this.length;
  var facePoints = [];
  for (var i = 0; i < faces; i++) {
    facePoints[i] = points[this[i]];
  }
  return facePoints;
};
// MathUtils
var MathUtils = {};
MathUtils.getRandomInt = function(min, max) {
  if (min > max) {
    var temp = min;
    min = max;
    max = temp;
  }
  var randomNumber = Math.random() * (max - min) + min;
  return Math.floor(randomNumber);
};
MathUtils.subtractVectors = function(vector0, vector1) {
  var vectorX = vector1.x - vector0.x;
  var vectorY = vector1.y - vector0.y;
  return new createjs.Point(vectorX, vectorY);
};
MathUtils.crossProduct2D = function(vector0, vector1) {
  return vector0.x * vector1.y - vector0.y * vector1.x;
}

コード2　マウスポインタの位置に応じて立方体をy軸およびx軸で回す

var stage;
var drawGraphics;
var points;
var angle = new createjs.Point();
var matrixX = new createjs.Matrix2D();
var matrixY = new createjs.Matrix2D();
var stageCenter = new createjs.Point();
var points2D = [];
var facesVertices;
var focalLength = 300;
function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  stageCenter.x = canvasElement.width / 2;
  stageCenter.y = canvasElement.height / 2;
  drawGraphics = createGraphics(stageCenter.x, stageCenter.y);
  points = createCubePoints(50);
  facesVertices = getFacesVertices();
  drawFaces(points, facesVertices);
  createjs.Ticker.addEventListener("tick", rotate);
  stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
  var mouseX = eventObject.stageX;
  var mouseY = eventObject.stageY;
  angle.y = (mouseX - stageCenter.x) / 300;
  angle.x = (mouseY - stageCenter.y) / -300;
}
function rotate(eventObject) {
  var count = points.length;
  points2D.length = 0;
  matrixY.identity().rotate(angle.y);
  matrixX.identity().rotate(angle.x);
  for (var i = 0; i < count; i++) {
    var point = points[i];
    point.rotatePoint(matrixY, "y");
    point.rotatePoint(matrixX, "x");  //
    points2D[i] = point.getProjetedPoint(focalLength);
  }
  drawFaces(points2D, facesVertices);
}
function drawFaces(points, faces) {
  var numFaces = faces.length;
  drawGraphics.clear();
  for (var i = 0; i < numFaces; i++) {
    var face = faces[i];
    var facePoints = face.getFacePoints(points);
    if (isFront(facePoints)) {
      draw(facePoints, face.color);
    }
  }
  stage.update();
}
function isFront(facePoints) {
  var origin = facePoints[0];
  var point0 = MathUtils.subtractVectors(origin, facePoints[1]);
  var point1 = MathUtils.subtractVectors(origin, facePoints[2]);
  return (0 <= MathUtils.crossProduct2D(point0, point1));
}
function draw(points, color) {
  var count = points.length;
  var point = points[count - 1];
  drawGraphics
  .beginFill(color)
  .moveTo(point.x, point.y);
  for (var i = 0; i < count; i++) {
    point = points[i];
    drawGraphics.lineTo(point.x, point.y);
  }
}
function createGraphics(x, y) {
  var drawShape = new createjs.Shape();
  drawShape.x = x;
  drawShape.y = y;
  stage.addChild(drawShape);
  return drawShape.graphics;
}
function createCubePoints(halfEdge) {
  var cubePoints = [
    new Point3D(-halfEdge, -halfEdge, -halfEdge),
    new Point3D(halfEdge, -halfEdge, -halfEdge),
    new Point3D(halfEdge, halfEdge, -halfEdge),
    new Point3D(-halfEdge, halfEdge, -halfEdge),
    new Point3D(-halfEdge, -halfEdge, halfEdge),
    new Point3D(halfEdge, -halfEdge, halfEdge),
    new Point3D(halfEdge, halfEdge, halfEdge),
    new Point3D(-halfEdge, halfEdge, halfEdge)
  ];
  return cubePoints;
}
function getFacesVertices() {
  var vertices = [
    new Face(0, 1, 2, 3, getRandomColor()),
    new Face(1, 5, 6, 2, getRandomColor()),
    new Face(4, 0, 3, 7, getRandomColor()),
    new Face(4, 5, 1, 0, getRandomColor()),
    new Face(6, 7, 3, 2, getRandomColor()),
    new Face(5, 4, 7, 6, getRandomColor())
  ];
  return vertices;
}
function getRandomColor() {
  return createjs.Graphics.getRGB(Math.floor(MathUtils.getRandomInt(0, 0xFFFFFF)));
}

第20回から3回にわたって取り組んできたお題は、これで仕上がった。jsdo.itにコードを掲げておこう。3つのクラスは[HTML]の欄に分けて書いた。次回は2次元平面に戻ろう。マウスポインタの動きに合わせて滑らかな線が描かれては消えてゆくサンプルを考えている。