前回の第23回
弾みのついた軌跡を描く
マウスポインタの動きに少し遅れて、
第23回コード2
var lastMidPoint = new createjs.Point();
var currentPoint = new createjs.Point();
var lastPoint = new createjs.Point();
var velocityX = 0;
var velocityY = 0;
var ease = 0.25;
var friction = 0.75;
function draw() {
var moveX = (stage.mouseX - currentPoint.x);
var moveY = (stage.mouseY - currentPoint.y);
if (moveX * moveX + moveY * moveY > 0.1) {
// velocityX = moveX * ease;
// velocityY = moveY * ease;
velocityX += moveX * ease;
velocityY += moveY * ease;
velocityX *= friction;
velocityY *= friction;
currentPoint.x += velocityX;
currentPoint.y += velocityY;
var midPoint = new createjs.Point((lastPoint.x + currentPoint.x) / 2, (lastPoint.y + currentPoint.y) / 2);
var myShape = getNewChild();
container.addChild(myShape);
drawCurve(myShape.graphics, lastMidPoint, midPoint, lastPoint);
lastPoint.initialize(currentPoint.x, currentPoint.y);
lastMidPoint.initialize(midPoint.x, midPoint.y);
}
stage.update();
}第23回コード2で、
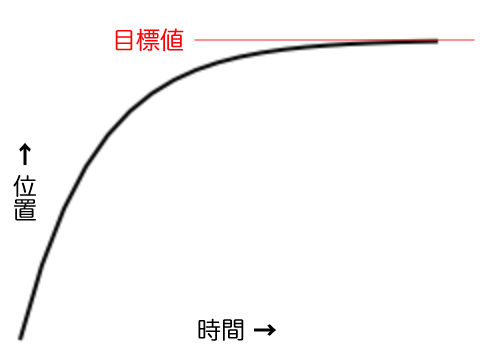
それに対して、
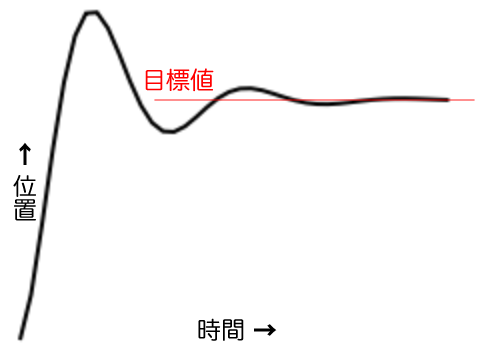
アニメーションを再描画するタイミング
前掲のコードを試してみると、
Ticker.
Ticker.
var maxLines = 100; // 50;
function initialize() {
createjs.Ticker.timingMode = createjs.Ticker.RAF;
createjs.Ticker.addEventListener("tick", draw);
}第23回コード2に手を加えてでき上がったのが、

var stage;
var container;
var children = [];
var lastMidPoint = new createjs.Point();
var currentPoint = new createjs.Point();
var lastPoint = new createjs.Point();
var velocityX = 0;
var velocityY = 0;
var ease = 0.25;
var friction = 0.75;
var maxLines = 100;
var currentLineThickness = 1;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
container = new createjs.Container();
stage.addChild(container);
lastPoint.x = lastMidPoint.x = canvasElement.width / 2;
lastPoint.y = lastMidPoint.y = canvasElement.height / 2;
createjs.Ticker.timingMode = createjs.Ticker.RAF;
createjs.Ticker.addEventListener("tick", draw);
}
function draw() {
var moveX = (stage.mouseX - currentPoint.x);
var moveY = (stage.mouseY - currentPoint.y);
var numChildren = container.getNumChildren();
if (moveX * moveX + moveY * moveY > 0.1) {
velocityX += moveX * ease;
velocityY += moveY * ease;
velocityX *= friction;
velocityY *= friction;
currentPoint.x += velocityX;
currentPoint.y += velocityY;
var midPoint = new createjs.Point((lastPoint.x + currentPoint.x) / 2, (lastPoint.y + currentPoint.y) / 2);
var myShape = getNewChild();
container.addChild(myShape);
drawCurve(myShape.graphics, lastMidPoint, midPoint, lastPoint);
lastPoint.initialize(currentPoint.x, currentPoint.y);
lastMidPoint.initialize(midPoint.x, midPoint.y);
if (numChildren >= maxLines){
removeOldChild();
}
} else if (numChildren > 1) {
removeOldChild();
}
stage.update();
}
function getNewChild() {
var child;
if (children.length) {
child = children.pop();
child.graphics.clear();
} else {
child = new createjs.Shape();
}
return child;
}
function removeOldChild() {
var child = container.getChildAt(0);
container.removeChildAt(0);
children.push(child);
}
function drawCurve(myGraphics, oldPoint, newPoint, controlPoint) {
setLineThickness(oldPoint, newPoint);
myGraphics.beginStroke("black")
.setStrokeStyle(currentLineThickness, "round", "round")
.moveTo(oldPoint.x, oldPoint.y)
.quadraticCurveTo(controlPoint.x, controlPoint.y, newPoint.x, newPoint.y);
}
function setLineThickness(oldPoint, newPoint) {
var distanceX = newPoint.x - oldPoint.x;
var distanceY = newPoint.y - oldPoint.y;
var distance = Math.sqrt(distanceX * distanceX + distanceY * distanceY);
var lineThickness = distance * 0.2;
currentLineThickness += (lineThickness - currentLineThickness) * 0.25;
}バネのような動きを数学の目で確かめる
最初の項
第23回
var ease = 0.25;
function draw() {
var moveX = (stage.mouseX - currentPoint.x);
var moveY = (stage.mouseY - currentPoint.y);
velocityX = moveX * ease;
velocityY = moveY * ease;
currentPoint.x += velocityX;
currentPoint.y += velocityY;
}それに対して、
もっとも、
var ease = 0.25;
var friction = 0.75;
function draw() {
var moveX = (stage.mouseX - currentPoint.x);
var moveY = (stage.mouseY - currentPoint.y);
// velocityX = moveX * ease;
// velocityY = moveY * ease;
velocityX += moveX * ease;
velocityY += moveY * ease;
velocityX *= friction;
velocityY *= friction;
currentPoint.x += velocityX;
currentPoint.y += velocityY;
}第23回コード2は位置に速度を加えてアニメーションさせた。前掲コード1もそれは同じだ。けれど、
コード1の加速度は、
この繰返しにより、
加速度を速度に加え、



