前回の回転するプロペラですが、ソースを見るとsinやらcosやらが出てきます。いわゆる三角関数というやつですが、得意な方は少ないかも知れません(中には見るとジンマシンが出るという方もいらっしゃるかも知れません)。
今回はこのあたりの座標操作を、直観的にわかるように解説していきましょう。
座標回転の基本
まず、座標について復習しておきましょう。普通、座標というのは「右に5、上に3」のような形を取ります。「右に5」の部分をx座標、「上に3」の部分をy座標と呼びます。
この座標で長方形を描くのは簡単です。ではなぜ前回のプログラムではややこしいことをしていたのでしょうか。それは、プロペラの回転は、x座標とy座標だけではできないからですね。どうすれば長方形を回転させた座標を計算できるでしょうか。
これには「右に5、上に3」というのを2つに分けて考えます。まず「右に5」の部分は(0, 0)から(5, 0)に移動します。続いて「上に3」の部分は(5, 0)から(5, 3)に移動します。当たり前ですね。
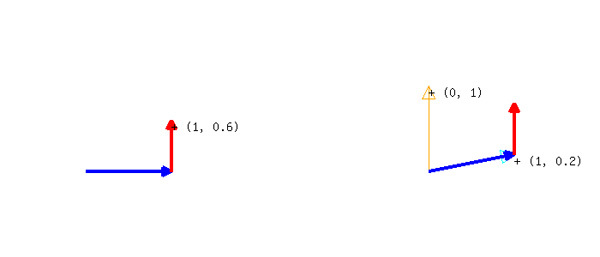
では「右に5」のときに、(0, 0)から(5, 0)に移動するのではなく、ちょっと曲がって(5, 1)に移動したらどうでしょう。
図1 (図内では数値は1/5になっています)
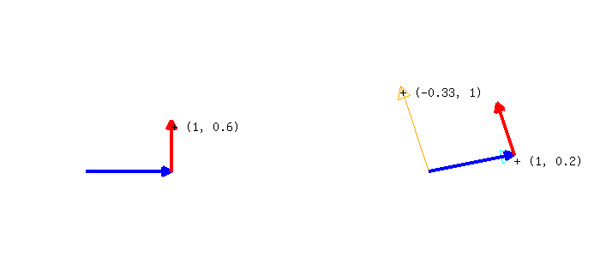
ついでに「上に3」のときに、(5, 1)から(5, 4)に移動するのではなく、ちょっと曲がって(4, 4)に移動してみたらどうでしょう。
図2
図で見ると、ちょっとひしゃげてはいますが、何とか回転に近付きました。でも、1つ1つの座標に、適当に1を足したり引いたりでは、うまくいきませんね。そこでたとえば
- 「右に1」は「右に1、上に0.25」に変換する
- 「上に1」は「上に1、右に-0.25」に変換する
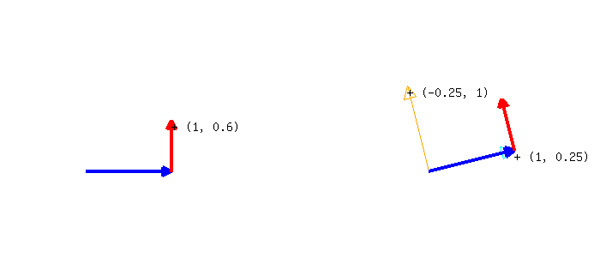
といったルールにしてみましょう。この場合、「右に5」は「右に5、上に1.25」(0.25×5=1.25)に変換されますので、(0, 0)から(5, 0)ではなく(5, 1.25)に移動します。「上に3」は「上に3、右に-0.75」に変換されますので、(5, 1.25)から(5, 4.25)ではなく(4.25, 4.25)に移動します。
図3
これは計算すると、移動後の矢印は元の矢印より少し長くなっているはずです。なのであとは長さを少し短くすればきちんと回転にできそうですね。「右に5、左に3」の部分を、長方形の頂点1つ1つにあてはめて変換すると、図4のようになります。これで、プロペラの回転の準備ができました。
図4
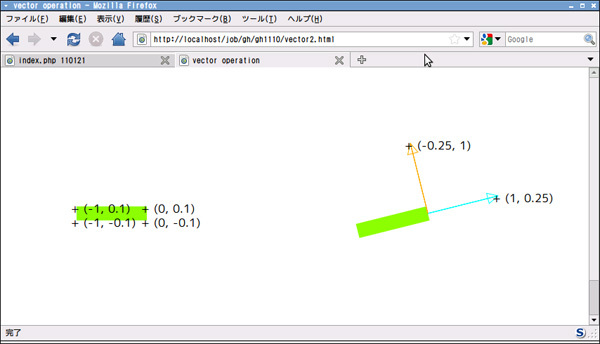
JavaScriptで座標の変換を試せるプログラムをこちらに用意しました。座標の数字の部分にマウスカーソルを持って行くとドラッグできますので、動かしてみてください。
角度を座標に変換するのが「三角関数」
さて、もう1つ大事なものが残っています。角度から座標に変換する方法です。これは詳しく解説してもいいのですが、使い方をおぼえれば十分なので、次のようにしてください。
- 「右に1」は「右にcos(a)、上にsin(a)」に変換
- 「上に1」は「右に-sin(a)、上にcos(a)」に変換
aは回転角ですが、単位は度ではありません。「角度(°)×円周率(3.14159…)÷180」で計算した数値です。ちなみに、上がプラスの座標系の場合は角度を増やすと左まわりに、下がプラスの座標系の場合は角度を増やすと右まわりになります。
たとえば、座標(x0, y0)を右に120°回転させるには、以下のようにします。今までは「上がプラス」でしたが、これは「下がプラス」になっていますので、角度が増えると右まわりに回転します。
PHPの場合
$a = 120 * 3.14159 / 180;
$x1 = cos($a) * $x0; # 右にx0
$y1 = sin($a) * $x0;
$x1 -= sin($a) * $y0; # 下にy0
$y1 += cos($a) * $y0;
JavaScriptの場合
var a = 120 * 3.14159 / 180;
var x1 = Math.cos(a) * x0; // 右にx0
var y1 = Math.sin(a) * x0;
x1 -= Math.sin(a) * y0; // 下にy0
y1 += Math.cos(a) * y0;
座標をx, yに分解して回転させる計算は、3Dにも応用できます。まずx座標とz座標を回転させて左右の視点を決め、次にy座標とz座標を回転させて上下の視点を決めます。こうして得られたz座標を、x座標とy座標の拡大縮小に使うと、遠いものほど小さくすることができます。これでx座標とy座標に変換されましたので、あとは2Dと同じ要領で描画できます。
次回は、今回の座標の変換のようすを動画にしてみたいと思います。ぜひご期待ください。







