はじめに
前回は、
目標
本連載では、
Java開発環境のセットアップ
手元にJavaの開発環境がなく、
NetBeansのインストール時にはJDK
ソースコードのダウンロード
今回作成するプログラムのソースコードは、
階層的クラスタリングの概要
今回は、
階層的クラスタリングとは、
階層的クラスタリングのアルゴリズムの手順を示すと、
- データ集合の中から、
互いの距離が最も近くなるデータ項目の対を探す。 - その項目対を、
1つのクラスタに統合する。 - そのクラスタと残りのデータ集合の中から、
互いの距離が最も近くなる要素対を探して統合する。 - 上記の処理を、
データ全体が1つのクラスタに統合されるまで繰り返す。
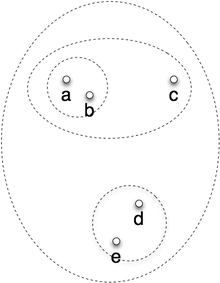
以上の手順によって、
各クラスタのノードが常に2つの子ノードを持つことから、
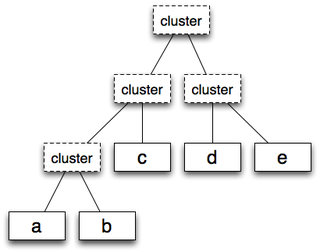
本連載では、
ベクトルクラスの作成
Javaの標準ライブラリには、
MultiVectorクラスは、
public class MultiVector {
private double[] data;
// 指定された次元数でゼロベクトルを作成
public MultiVector(int dimension) {
data = new double[dimension];
}
// 次元数チェック
private void checkDimension(MultiVector v) {
if (dimension() != v.dimension()) {
throw new IllegalArgumentException("Dimension mismatch.");
}
}
// 指定されたベクトルを加算
public void add(MultiVector v) {
checkDimension(v);
for (int i = 0; i < dimension(); i++) {
data[i] += v.data[i];
}
}
...
}MultiVectorには、
- void add(MultiVector v)
- ベクトルにvを加算します。
- void subtract(MultiVector v)
- ベクトルからvを減算します。
- void multiply(double d)
- ベクトル成分をd倍します。
- void divide(double d)
- ベクトル成分をdで除算します。
- double norm()
- ベクトルのノルム
(長さ) を計算します。 - void normalize()
- ベクトルを正規化します
(ノルムが1になるように調整します)。 - double distanceSq(MultiVector v)
- このベクトルとvの距離の二乗を計算します。
ノードクラスの作成
次に、
まず、
public interface Node {
List<MultiVector> getVectors();
}次に、
public class Item implements Node {
private String name; // 結果出力用のプロパティ
private MultiVector vector;
public Item(String name, MultiVector vector) {
this.name = name;
this.vector = vector;
}
public String getName() { return name; }
public MultiVector getVector() { return vector; }
public List<MultiVector> getVectors() {
// ベクトル自身をリスト化して返す
return Collections.singletonList(vector);
}
}同様に、
public class Cluster implements Node {
private Node left;
private Node right;
private List<MultiVector> cachedVectors;
public Cluster(Node left, Node right) {
this.left = left;
this.right = right;
}
public Node getLeft() { return left; }
public Node getRight() { return right; }
public List<MultiVector> getVectors() {
// 高速化のため結果をキャッシュする
if (cachedVectors == null) {
cachedVectors = new ArrayList<MultiVector>();
// leftノードとrightノードのベクトル集合を連結
cachedVectors.addAll(left.getVectors());
cachedVectors.addAll(right.getVectors());
}
return cachedVectors;
}
}距離関数クラスの作成
さて、
この距離の計算には、
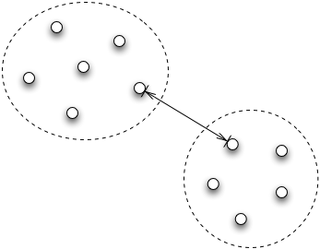
戦略を後で簡単に切り替えられるように、 このインターフェイスを実装し、 このdistanceメソッドでは、 ベクトル、 上のbuildメソッドは、 それでは、 クラスタリングの実行結果は、 以上を行うDemoクラスは、 Demoクラスを実行すると、 いかがでしょうか。ブルーとシアン、 今回作成した階層的クラスタリングのプログラムは、 今回は、 次回は視覚的な観点にフォーカスを移し、public interface DistanceEvaluator {
double distance(Node n1, Node n2);
}public class NearestDistanceEvaluator implements DistanceEvaluator {
public double distance(Node n1, Node n2) {
double minDistSq = Double.MAX_VALUE;
for (MultiVector v1 : n1.getVectors()) {
for (MultiVector v2 : n2.getVectors()) {
// 全てのベクトルの組み合わせに対して距離を計算
double distSq = v1.distanceSq(v2);
// 最小となる距離を採用
if (distSq < minDistSq) {
minDistSq = distSq;
}
}
}
return Math.sqrt(minDistSq);
}
}階層的クラスタリングの実装
public class ClusterBuilder {
private DistanceEvaluator distanceEvaluator;
public ClusterBuilder(DistanceEvaluator distanceEvaluator) {
this.distanceEvaluator = distanceEvaluator;
}
public Node build(List<? extends Node> nodes) {
// ノードが1つに集約されるまで繰り返す
while (nodes.size() > 1) {
Node merge1 = null;
Node merge2 = null;
double minDist = Double.MAX_VALUE;
// 距離が最小となるノード対を探す
for (int i = 0; i < nodes.size(); i++) {
Node n1 = nodes.get(i);
for (int j = i + 1; j < nodes.size(); j++) {
Node n2 = nodes.get(j);
double dist = distanceEvaluator.distance(n1, n2);
if (dist < minDist) {
merge1 = n1;
merge2 = n2;
minDist = dist;
}
}
}
// 次ステップ用のノードリストを作成
List<Node> nextNodes = new ArrayList<Node>();
for (Node node : nodes) {
// 統合対象にならなかったノードを追加
if (node != merge1 && node != merge2) {
nextNodes.add(node);
}
}
// 統合対象のノード対をクラスタ化して追加
nextNodes.add(new Cluster(merge1, merge2));
nodes = nextNodes;
}
return nodes.get(0);
}
}色集合の階層的クラスタリング
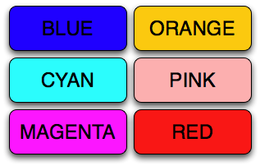
public class Demo {
public static void main(String[] args) {
new Demo().run();
}
public void run() {
// 入力データを作成
List<Item> input = new ArrayList<Item>();
input.add(new Item("BLUE", colorToVector(Color.BLUE)));
input.add(new Item("CYAN", colorToVector(Color.CYAN)));
input.add(new Item("MAGENTA", colorToVector(Color.MAGENTA)));
input.add(new Item("ORANGE", colorToVector(Color.ORANGE)));
input.add(new Item("PINK", colorToVector(Color.PINK)));
input.add(new Item("RED", colorToVector(Color.RED)));
// 最短距離法に基づく階層的クラスタリングを準備
DistanceEvaluator evaluator = new NearestDistanceEvaluator();
ClusterBuilder builder = new ClusterBuilder(evaluator);
// クラスタリングを実行
Node result = builder.build(input);
// クラスタリング結果を表示
output(result, 0);
}
private MultiVector colorToVector(Color c) {
// 色成分を3次元のベクトルに変換
return new MultiVector(c.getRed(), c.getGreen(), c.getBlue());
}
private void output(Node node, int depth) {
// インデントを表示
for (int i = 0; i < depth; i++) {
System.out.print(" ");
}
if (node instanceof Item) {
// 末端ノードなら項目名を表示
System.out.println(((Item) node).getName());
} else if (node instanceof Cluster) {
// クラスタなら"+"を表示し、子ノードを再帰的に表示
System.out.println("+");
Cluster cluster = (Cluster) node;
output(cluster.getLeft(), depth + 1);
output(cluster.getRight(), depth + 1);
}
}
}+
+
RED
+
MAGENTA
+
ORANGE
PINK
+
BLUE
CYAN
まとめと次回予告



