はじめに
前回は、
今回からは、
ソースコードのダウンロード
今回作成するプログラムのソースコードは、
ツリーマップの概要
ツリーマップ
ツリーマップを利用した情報可視化の有名な例としては、

また、
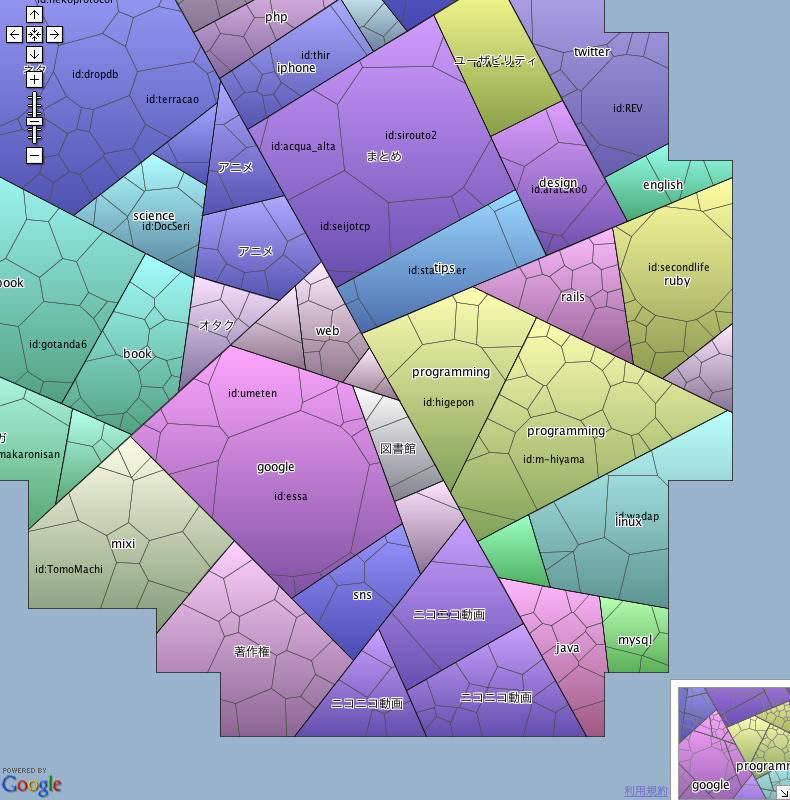
なお、
ツリーマップの長所
ツリーマップは、
1つ目の利点は、
2つ目の利点は、
二分木のツリーマップ
前回解説した階層的クラスタリングでは、
それでは早速、
1. ツリーマップの各領域の面積を決めるため、
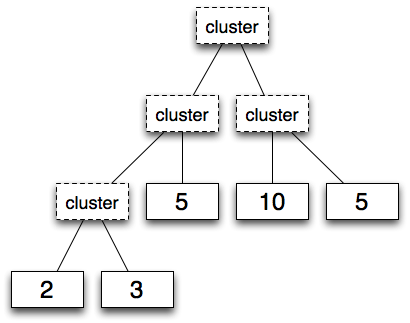
2. ツリー全体を格納する大きな長方形を用意する。
3. 長方形を、

このとき、
- 現在の長方形が横長ならば、
左右に分割する - 現在の長方形が縦長ならば、
上下に分割する
4. 分割後の長方形と対応する子ノードについて、
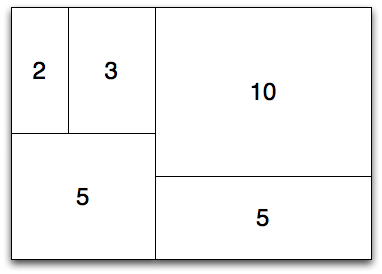
処理対象のツリー構造を二分木に限定した場合、
階層的クラスタリングの手直し
ツリーマップの描画に先立って、
ノードサイズの導入
クラスタリングのノードを示すNodeインターフェイスに、
public interface Node {
List getVectors();
double getArea();
} このgetArea()メソッドを、
public class Item {
private String name;
private MultiVector vector;
private double area;
public Item(String name, MultiVector vector, double area) {
this.name = name;
this.vector = vector;
this.area = area;
}
public double getArea() { return area; }
...
}次にClusterクラスでは、
public class Cluster {
private Node left;
private Node right;
public double getArea() {
return left.getArea() + right.getArea();
}
...
}色データに特化したノードクラスの導入
次回のツリーマップの実践では、
public class ColorItem extends Item {
private Color color;
public ColorItem(Color color, double area) {
super(color.toString(), colorToVector(color), area);
this.color = color;
}
private static MultiVector colorToVector(Color c) {
return new MultiVector(c.getRed(), c.getGreen(), c.getBlue());
}
public Color getColor() { return color; }
}ColorItemクラスでは、
Ward法の導入
前回は、
Ward法では、
d(C1, C2) = E(C1 | C2) - {E(C1) + E(C2)}
C1: クラスタ1
C2: クラスタ2
C1 | C2: C1とC2を統合したクラスタ
E(X): クラスタXの重心と、
式や言葉で説明するよりも、
public class WardDistanceEvaluator implements DistanceEvaluator {
public double distance(Node n1, Node n2) {
double s12 = sumCentroidDistanceSq(new Cluster(n1, n2));
double s1 = sumCentroidDistanceSq(n1);
double s2 = sumCentroidDistanceSq(n2);
return s12 - (s1 + s2);
}
private double sumCentroidDistanceSq(Node n) {
List vectors = n.getVectors();
// ノードに含まれる全ベクトルの平均値を求め、クラスタの重心とする
MultiVector center = new MultiVector(vectors.get(0).dimension());
for (MultiVector vector : vectors) {
center.add(vector);
}
center.divide(vectors.size());
// ノードに含まれる各ベクトルと重心の距離の二乗の総和を計算
double sum = 0;
for (MultiVector vector : vectors) {
sum += vector.distanceSq(center);
}
return sum;
}
} 後編に続く
今回は、ツリーマップの概要と、そのアルゴリズムの基本的な考え方を説明しました。また、ツリーマップを実践する準備段階として、前回作成した階層的クラスタリングのプログラムに機能追加を行いました。
後編となる次回は、これまでのプログラムを元にして、いよいよツリーマップの描画へと入っていきます。お楽しみに!



