前回 は、座標を考えるときは、どこから見た値なのか意識しなければならないことを説いた。そのうえで、自分を中心とした天動説のプロパティと、自分の存在する空間で考える地動説のプロパティとを区別し、地動説に基準を合わせて座標の計算を試みた。
今回はその続きとして、天動説を基準とした座標計算から始めよう。そして、減速しながら目的の値に近づくイージングのアニメーションについて解説したい。
天動説で座標空間を一致させる
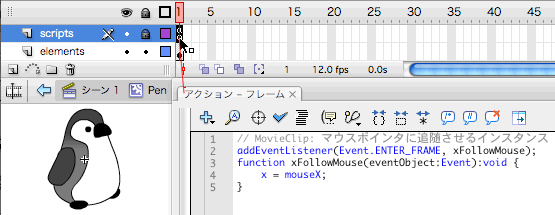
まずは、前回確認した天動説と地動説のプロパティを区別せずに記述したスクリプトの例だ。自分の配置された親の座標空間を基準とする地動説のプロパティDisplayObject.x に、自分の基準点から見た天動説の座標を示すDisplayObject.mouseX プロパティの値が代入されている(図1 ) 。
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
x = mouseX;
}
図1 地動説のプロパティに単純に天動説のプロパティ値を代入[ムービープレビュー]を見ると、代入式の両辺の基準が合っていないために、点滅したようなアニメーションになった。そこで、前回は地動説で基準を合わせようと、右辺のプロパティDisplayObject.mouseX のターゲットに親のタイムライン(DisplayObject.parent )を指定した。
しかし、今回は天動説を基準とするので、この右辺は変えない。そのうえで行う修正は、きわめてシンプルだ。先に結果を見てしまおう。
xfunction xFollowMouse(eventObject:Event):void {
x += mouseX;
}
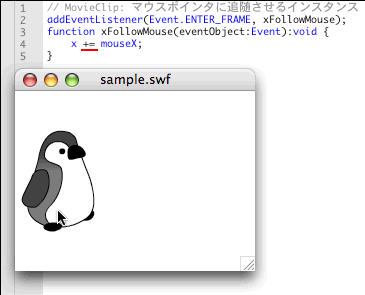
代入の演算子が、普通の代入=ではなく、加算後代入演算子+=になっていることに注目してほしい。早速[ムービープレビュー]を確かめると、意図したとおりに、インスタンスがマウスポインタの水平座標に追随する。さて、演算子を変えただけで、なぜふたつのプロパティの基準が一致したのだろう。
図2 地動説のプロパティに天動説のプロパティ値を加算後代入たとえば、先日の箱根駅伝でランナーが、先頭走者に追いつこうとすると、まず相手の位置を知らなければならない。そのとき、ひとつは先頭走者のスタート地点からの位置を調べることが考えられる。もちろん、その位置は刻々と変化する。そこに可能なかぎり速く達しようとすれば、先頭走者に追いつくことができる。スタート地点からの位置というのは、地動説の基準である。
しかし、マラソンなどの場合には、もうひとつの情報の捉え方の方が端的だろう。それは、先頭走者と自分の間が、どれくらい離れているかを知ることだ。その差を速く走ることにより埋めれば、すなわち追いつくということになる。こちらが、天動説の基準になる。
DisplayObject.mouseX プロパティの値は天動説の基準で、自分の位置から見たマウスポインタの座標、つまりマウスポインタと自分との間の座標の差である。加算後打入演算子+=でその値をDisplayObject.x プロパティに代入するというのは、自分の現在位置にその差を足し込んで埋める処理になる。その結果、インスタンスはマウスポインタに追いつくのである[1] 。
わかったところで、水平・垂直座標を合わせて、インスタンスがマウスポインタに追随するスクリプトを、天動説基準で完成させよう(スクリプト1 ) 。[ムービープレビュー]で確認すると、インスタンスがマウスポインタに追随する。
スクリプト1 MovieClipインスタンスをマウスポインタの動きに追随させる―天動説// MovieClip: マウスポインタに追随させるインスタンス
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
x += += [1] たとえば、DisplayObject.mouseX プロパティの値が100だったとする。それは、マウスポインタと自分との間の座標の差なので、その値100をDisplayObject.x に加算すれば、差がなくなって結果として追いつく(図3 ) 。
イーズアウトの公式
インスタンスを動かす場合、いきなり目的の値に達するのではなく、徐々に加速あるいは減速しながら近づくという表現がFlash使いには好まれるようだ。そこで、比較的よく用いられる減速しながら目的の値に至る、いわゆる「イーズアウト」の基本的な処理方法を紹介しよう。
このスクリプトも、まず結果を見てしまった方がわかりやすい。前述スクリプト1に、減速(deceleration)の度合いを調整する変数nDecelerationの宣言を加える。この減速率の変数nDecelerationは、インスタンスの座標プロパティへの代入式の右辺、つまりマウスポインタの座標値に掛合わせる(スクリプト2 ) 。
減速率には、0から1の間の値を設定する。1であれば、スクリプト1の動作と変わらず、遅れなくマウスポインタに追随する。0に近いほど、ゆっくりと減速しながら、後を追いかけることになる(もちろん、0であれば動かない) 。スクリプト2では、0.2とした。
スクリプト2 MovieClipインスタンスを減速しながらマウスポインタに追随させる―イーズアウト// MovieClip: マウスポインタに追随させるインスタンス
var nDeceleration:Number = 0.2 ;
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
x += mouseX*nDeceleration ;
y += mouseY*nDeceleration ;
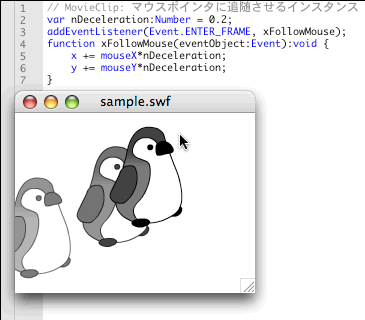
}[ムービープレビュー]を見ると、インスタンスはマウスポインタを少し遅れながら追いかけ、近づくにつれてスピードは遅くなる。イーズアウトのアニメーションだ(図4 ) 。つぎに、なぜ減速するのかを説明しよう。
図4 インスタンスはマウスポインタに遅れて減速しながら追随する昔筆者の隣の家に、男の子の兄弟がいた。兄弟というのは、大抵は下の子が要領はよい。あるとき、弟が茶の間のお菓子を見て、台所の母親に「お菓子食べてもいい?」と尋ねた。ふたり兄弟なので、「 半分ずつよ」と母親は答えた。しかし、しばらくするとまた、「 お菓子食べてもいい?」と聞く。「 半分だからね」と念を押すと、またすぐ「お菓子食べてもいい?」と繰返す。
あまりしつこいので、母親が茶の間に行くと、お菓子はほぼなくなっていたという。どうやら「半分よ」と母親の答えが返ってくるたびに、残ったお菓子を半分ずつ食べてしまっていたらしい。
これは、減速率0.5(=1/2)の場合の処理だ。母親の「半分ずつよ」という答えをイベントに、毎回お菓子を半分消費した訳である。この処理の結果として、第1にお菓子はどんどん減っていき、残りはかぎりなく0に近づく。しかし第2に、残りが減る訳であるから、毎回食べられる量は半減して少なくなっていく。
つまり、目的の値にかぎりなく近づきつつ[2] 、その近づくスピードは次第に遅くなるというイーズアウトの処理が実現するのである。
さて、前記スクリプト2では、天動説の座標計算をもとに、イーズアウトの処理を加えた。しかし、もちろん地動説の計算の仕方でも、イーズアウトのアニメーションを表現することは可能だ。とくに、目的のプロパティ値が予め決まっているときは、地動説で考えた方が式は立てやすい。
たとえば、ステージの端から中央に、イーズアウトで移動するアニメーションを考えてみよう。まず、目的のステージ中央の座標は、Stageクラスのプロパティから計算できる。ステージの幅と高さが、それぞれStage.stageWidth とStage.stageHeight プロパティで調べられる(図5 [3] )ので、それぞれを2で割ればよい。
図5 [ActionScript 3.0コンポーネントリファレンスガイド]の[Stageクラス]の項 ただし、Stageのインスタンスを取得する方法には、注意が必要だ。StageインスタンスはFlash Playerにただひとつ存在し、追加して作成することはできない。インスタンスのDisplayObject.stage からアクセスする必要がある。
以上を前提として、ステージ中央にインスタンスをイーズアウトでアニメーションさせるスクリプトは、以下のとおりだ(スクリプト3 [4] ) 。目的の座標から自身の座標を引く処理は、地動説の計算になる。
スクリプト3 MovieClipインスタンスを減速しながらステージ中央に移動させる
// MovieClip: 移動させるインスタンス
var nCenterX :Number = stage.stageWidth nCenterY :Number = stage.stageHeight (nCenterX-x) *nDeceleration;
y += (nCenterY-y) *nDeceleration;
}MovieClipインスタンスをステージの端に配置したうえで[ムービープレビュー]を確認すると、インスタンスはイーズアウトしながらステージ中央に移動する。最後に、イーズアウトの処理の計算式を公式風にまとめておこう(表1 ) 。
表1 イーズアウトの公式
目指すプロパティ値に減速しながら到達する プロパティ += 自分から見た相手との差*減速率
または、
プロパティ += ( 相手の値 - 自分の値)*減速率
ただし、0 < 減速率 < 1とする。
[2] 数学的に考えると、目的の値にかぎりなく近づきつつも、その差(残り)が0になることはない。しかし、Flashの座標の計算などでは、小数点以下の一定の範囲(インスタンスの座標の場合には小数点以下2桁)で誤差が丸められるため、最終的に差が0になることも少なくない。
今回解説した次のサンプルファイルがダウンロードできます。
![図5 [ActionScript 3.0コンポーネントリファレンスガイド]の[Stageクラス]の項 図5 [ActionScript 3.0コンポーネントリファレンスガイド]の[Stageクラス]の項](/assets/images/dev/serial/01/as3/0010/thumb/TH800_Gihyo080101-003.gif)



