今回から、
[プロパティ]インスペクタを使った3次元空間の操作
コンピュータグラフィックス
だが、
![図1 [プロパティ]インスペクタの[3D位置とビュー]セクションで3次元表現を操作 図1 [プロパティ]インスペクタの[3D位置とビュー]セクションで3次元表現を操作](/assets/images/dev/serial/01/as3/0033/thumb/TH400_001.png)
これは、
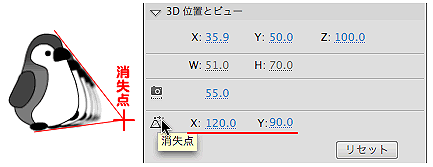
[プロパティ]インスペクタの[3D位置とビュー]セクションには、
![図3 [プロパティ]インスペクタの[3D位置とビュー]セクションにおける[遠近の角度] 図3 [プロパティ]インスペクタの[3D位置とビュー]セクションにおける[遠近の角度]](/assets/images/dev/serial/01/as3/0033/thumb/TH800_003.png)
ステージにランダムなシェイプを配置する
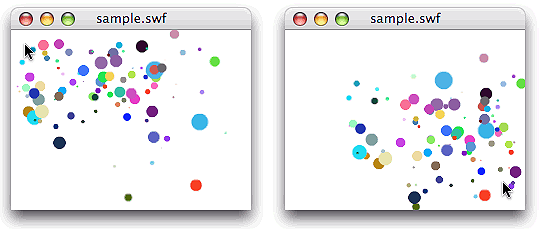
遠近法を操作すると表現がどう変わるかは、
Shape.
Graphicsオブジェクト.beginFill(カラー値, アルファ値)カラーは通常16進数の整数、
Graphicsオブジェクト.drawCircle(中心のx座標値, 中心のy座標値, 半径の長さ)これらの知識をもとにして、
// フレームアクション
function xCreateCircle(nRadius:Number, nColor:uint = 0):Shape {
var myShape:Shape = new Shape();
var myGraphics:Graphics = myShape.graphics;
myGraphics.beginFill(nColor);
myGraphics.drawCircle(0, 0, nRadius);
myGraphics.endFill();
return myShape;
}同じタイムラインのフレームアクションからつぎのように関数xCreateCircle()を呼び出すと、
var myShape:Shape = xCreateCircle(10, 0x0000FF);
addChild(myShape);
myShape.x = stage.stageWidth / 2;
myShape.y = stage.stageHeight / 2;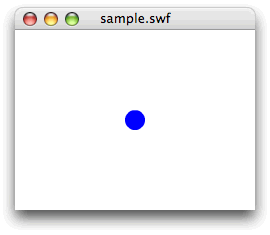
このShapeインスタンスをいくつもステージ上につくるとき、
Math.random() * (最大値 - 最小値) + 最小値カラー値は整数にする必要がある。ランダムな整数値を求める場合、
Math.floor(Math.random() * (最大値 - 最小値 + 1) + 最小値)そこで、
function xGetRandom(nMax:Number = 1, nMin:Number = 0, bInt:Boolean = false):Number {
if (nMax < nMin) {
var nTemp:Number = nMax;
nMax = nMin;
nMin = nTemp;
}
var nRandom:Number = Math.random();
if (bInt) {
return Math.floor(nRandom * (nMax - nMin + 1) + nMin);
} else {
return nRandom * (nMax - nMin) + nMin;
}
}以下のスクリプト1には、
// タイムライン: メイン
// フレームアクション
xCreateShapes(100);
function xCreateShapes(nCount:uint):void {
for (var i:uint = 0; i < nCount; i++) {
var nColor:uint = xGetRandom(0xFFFFFF, 0, true);
var nRadius:Number = xGetRandom(10);
var myShape:Shape = xCreateCircle(nRadius, nColor);
addChild(myShape);
myShape.x = xGetRandom(stage.stageWidth);
myShape.y = xGetRandom(stage.stageHeight);
myShape.z = xGetRandom(stage.stageWidth);
}
}
function xCreateCircle(nRadius:Number, nColor:uint = 0):Shape {
var myShape:Shape = new Shape();
var myGraphics:Graphics = myShape.graphics;
myGraphics.beginFill(nColor);
myGraphics.drawCircle(0, 0, nRadius);
myGraphics.endFill();
return myShape;
}
function xGetRandom(nMax:Number = 1, nMin:Number = 0, bInt:Boolean = false):Number {
if (nMax < nMin) {
var nTemp:Number = nMax;
nMax = nMin;
nMin = nTemp;
}
var nRandom:Number = Math.random();
if (bInt) {
return Math.floor(nRandom * (nMax - nMin + 1) + nMin);
} else {
return nRandom * (nMax - nMin) + nMin;
}
}
もっとも、
PerspectiveProjectionクラスで遠近法を操作する
PerspectiveProjectionクラスを使って、
まず、

それでは、
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
addEventListener(Event.ENTER_FRAME, xMoveViewPoint);
function xMoveViewPoint(eventObject:Event):void {
myPerspective.projectionCenter = new Point(mouseX, mouseY);
}
さらに、
var standardView:Number = myPerspective.fieldOfView;
var bStandard:Boolean = true;
stage.addEventListener(MouseEvent.CLICK, xChangeFieldOfView);
function xChangeFieldOfView(eventObject:MouseEvent):void {
if (bStandard = ! bStandard) {
myPerspective.fieldOfView = standardView;
} else {
myPerspective.fieldOfView = standardView + 50;
}
}
なお、
さて、
// タイムライン: メイン
// フレームアクション
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var standardView:Number = myPerspective.fieldOfView;
var bStandard:Boolean = true;
addEventListener(Event.ENTER_FRAME, xMoveViewPoint);
stage.addEventListener(MouseEvent.CLICK, xChangeFieldOfView);
xGreateShapes(100);
function xMoveViewPoint(eventObject:Event):void {
myPerspective.projectionCenter = new Point(mouseX, mouseY);
}
function xChangeFieldOfView(eventObject:MouseEvent):void {
if (bStandard = ! bStandard) {
myPerspective.fieldOfView = standardView;
} else {
myPerspective.fieldOfView = standardView + 50;
}
}
function xGreateShapes(nCount:uint):void {
for (var i:uint = 0; i < nCount; i++) {
var nColor:uint = xGetRandom(0xFFFFFF, 0, true);
var nRadius:Number = xGetRandom(10);
var myShape:Shape = xCreateCircle(nRadius, nColor);
addChild(myShape);
myShape.x = xGetRandom(stage.stageWidth);
myShape.y = xGetRandom(stage.stageHeight);
myShape.z = xGetRandom(stage.stageWidth);
}
}
function xCreateCircle(nRadius:Number, nColor:uint = 0):Shape {
var myShape:Shape = new Shape();
var myGraphics:Graphics = myShape.graphics;
myGraphics.beginFill(nColor);
myGraphics.drawCircle(0, 0, nRadius);
myGraphics.endFill();
return myShape;
}
function xGetRandom(nMax:Number = 1, nMin:Number = 0, bInt:Boolean = false):Number {
if (nMax < nMin) {
var nTemp:Number = nMax;
nMax = nMin;
nMin = nTemp;
}
var nRandom:Number = Math.random();
if (bInt) {
return Math.floor(nRandom * (nMax - nMin + 1) + nMin);
} else {
return nRandom * (nMax - nMin) + nMin;
}
}ところで、
したがって、
今回解説した次のサンプルファイルがダウンロードできます。
- スクリプト1および2サンプルファイル
(CS4形式/ 約16KB)



