今回は、

内積から射影を取出す
まず直線の場合なら、
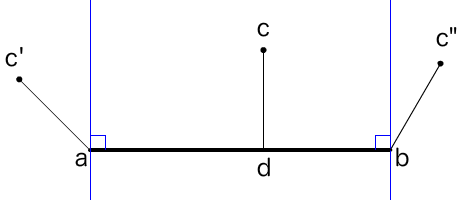
ふたつの垂線の内側
ここで、
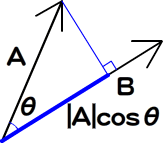
第51回図6では、
つまり、
内積による場合分けと線分との距離
内積を使って線分に対する3つの領域を分け、
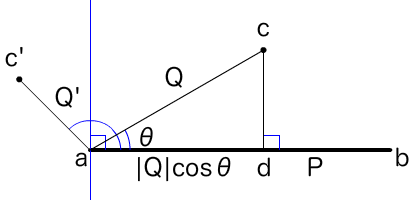
まず、
ベクトルPとQの内積が正数なら、
そして、
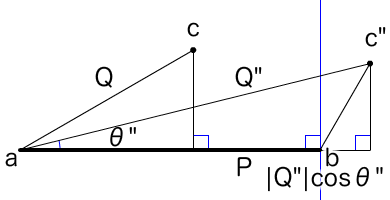
任意の1点と線分の両端の座標から線分上のもっとも近い点を返す関数の定義
計算の仕方はわかったので、スクリプトを書こう。まず、任意の座標から線分上のもっとも近い点を返す関数の定義だ。引数には、Pointオブジェクトで座標を3つ渡す。第1引数が任意の座標で、第2と第3引数は線分の両端の座標とする。関数名はxGetClosestPoint()とした。- xGetClosestPoint
(任意の点, 線分の始点, 線分の終点)
以下のスクリプト1はフレームアクションに関数xGetClosestPoint()を定めた。計算の手順は前項に述べたとおりである。
// フレームアクション
function xGetClosestPoint(myPoint:Point, begin:Point, end:Point):Point {
var myVector3D:Vector3D = new Vector3D(myPoint.x - begin.x, myPoint.y - begin.y);
var baseVector3D:Vector3D = new Vector3D(end.x - begin.x, end.y - begin.y);
var nDotProduct:Number = myVector3D.dotProduct(baseVector3D);
if (nDotProduct > 0) {
var nBaseLength:Number = baseVector3D.length;
var nProjection:Number = nDotProduct / nBaseLength;
if (nProjection < nBaseLength) {
baseVector3D.scaleBy(nProjection / nBaseLength);
return new Point(begin.x + baseVector3D.x, begin.y + baseVector3D.y);
} else {
return end;
}
} else {
return begin;
}
}まず、
あとは、
入れ子のif条件は、
- Vector3Dオブジェクト.scaleBy
(乗数)
そのVector3Dオブジェクトのxy座標に線分の始点の座標を加えれば、
インスタンスを折れ線に沿ってドラッグする
いよいよ仕上げだ。お題に述べたとおり、
// フレームアクションに追加
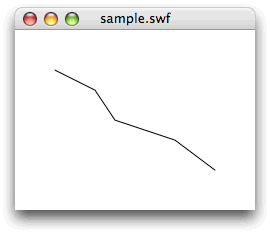
var vertices:Vector.<Point> = new Vector.<Point>();
vertices.push(new Point(40, 40));
vertices.push(new Point(80, 60));
vertices.push(new Point(100, 90));
vertices.push(new Point(160, 110));
vertices.push(new Point(200, 140));
var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
addChildAt(mySprite, 0);
myGraphics.lineStyle(1, 0);
myGraphics.moveTo(vertices[0].x, vertices[0].y);
for (var i:uint = 1; i < vertices.length; i++) {
myGraphics.lineTo(vertices[i].x, vertices[i].y);
}
折れ線の座標はPointオブジェクトにして、
仕上げは、
// フレームアクションに追加
var nStart:Number = new Point(stage.stageWidth, stage.stageHeight).length;
var my_mc:MovieClip;
my_mc.x = vertices[0].x;
my_mc.y = vertices[0].y;
my_mc.addEventListener(MouseEvent.MOUSE_DOWN, xStartMove);
function xStartMove(eventObject:MouseEvent):void {
my_mc.addEventListener(Event.ENTER_FRAME, xMove);
stage.addEventListener(MouseEvent.MOUSE_UP, xStopMove);
}
function xStopMove(eventObject:MouseEvent):void {
my_mc.removeEventListener(Event.ENTER_FRAME, xMove);
stage.removeEventListener(MouseEvent.MOUSE_UP, xStopMove);
}
function xMove(eventObject:Event):void {
var nClosest:Number = nStart;
var mousePoint:Point = new Point(mouseX, mouseY);
var nLength:uint = vertices.length - 1;
for (var i:uint = 0; i < nLength; i++) {
var currentPoint:Point =
xGetClosestPoint(mousePoint, vertices[i], vertices[i + 1]);
var nDistance:Number = mousePoint.subtract(currentPoint).length;
if (nDistance <= nClosest) {
var closestPoint:Point = currentPoint;
nClosest = nDistance;
}
}
my_mc.x = closestPoint.x;
my_mc.y = closestPoint.y;
}イベントInteractiveObject.
関数xMove()は、
- Pointオブジェクト.subtract
(差引くPointオブジェクト)
調べた距離がこれまでの線分より短ければ、
なお、
// フレームアクション: メインタイムライン
function xGetClosestPoint(myPoint:Point, begin:Point, end:Point):Point {
var myVector3D:Vector3D = new Vector3D(myPoint.x - begin.x, myPoint.y - begin.y);
var baseVector3D:Vector3D = new Vector3D(end.x - begin.x, end.y - begin.y);
var nDotProduct:Number = myVector3D.dotProduct(baseVector3D);
if (nDotProduct > 0) {
var nBaseLength:Number = baseVector3D.length;
var nProjection:Number = nDotProduct / nBaseLength;
if (nProjection < nBaseLength) {
baseVector3D.scaleBy(nProjection / nBaseLength);
return new Point(begin.x + baseVector3D.x, begin.y + baseVector3D.y);
} else {
return end;
}
} else {
return begin;
}
}
var vertices:Vector.<Point> = new Vector.<Point>();
vertices.push(new Point(40, 40));
vertices.push(new Point(80, 60));
vertices.push(new Point(100, 90));
vertices.push(new Point(160, 110));
vertices.push(new Point(200, 140));
var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
addChildAt(mySprite, 0);
myGraphics.lineStyle(1, 0);
myGraphics.moveTo(vertices[0].x, vertices[0].y);
for (var i:uint = 1; i < vertices.length; i++) {
myGraphics.lineTo(vertices[i].x, vertices[i].y);
}
var nStart:Number = new Point(stage.stageWidth, stage.stageHeight).length;
var my_mc:MovieClip;
my_mc.x = vertices[0].x;
my_mc.y = vertices[0].y;
my_mc.addEventListener(MouseEvent.MOUSE_DOWN, xStartMove);
function xStartMove(eventObject:MouseEvent):void {
my_mc.addEventListener(Event.ENTER_FRAME, xMove);
stage.addEventListener(MouseEvent.MOUSE_UP, xStopMove);
}
function xStopMove(eventObject:MouseEvent):void {
my_mc.removeEventListener(Event.ENTER_FRAME, xMove);
stage.removeEventListener(MouseEvent.MOUSE_UP, xStopMove);
}
function xMove(eventObject:Event):void {
var nClosest:Number = nStart;
var mousePoint:Point = new Point(mouseX, mouseY);
var nLength:uint = vertices.length - 1;
for (var i:uint = 0; i < nLength; i++) {
var currentPoint:Point =
xGetClosestPoint(mousePoint, vertices[i], vertices[i + 1]);
var nDistance:Number = mousePoint.subtract(currentPoint).length;
if (nDistance <= nClosest) {
var closestPoint:Point = currentPoint;
nClosest = nDistance;
}
}
my_mc.x = closestPoint.x;
my_mc.y = closestPoint.y;
}これで、

今回解説した次のサンプルファイルがダウンロードできます。
- スクリプト1のサンプルファイル
(CS5形式/約12KB)



