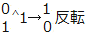技術評論社より発売された拙著『ActionScript 3.0パフォーマンスチューニング』から、ActionScript 3.0の最適化の仕方をご紹介する特別編は今回で終わりとなる。結びとして、数値演算のうち2進法の計算を解説したい。コンピュータは内部的に2進数で演算している。そのため、数値を2進数で扱えばコンピュータにより近い計算になり、お得なことが少なくない。他方で、考え方を正しく理解しないと、サンプルだけ見ても使いこなすのは難しい。
2進数とは
まずは、2進数を数学的に式で表そう。といっても、さほど難しいことはない。小学校の算数で、数は10の束ができると1繰り上がると習った。これが10進法だ。たとえば、10進数の123はつぎの式で表せる。
123=1×100+2×10+3×1=1×102+2×101+3×100
2進法は2の束で繰り上げればよい。たとえば、2進数の1011は、同じように式で表せば、10進数の11だとわかる。
1011(2進数)=1×23+0×22+1×21+1×20=8+0+2+1=11(10進数)
もっと一般的に、k桁目の数をnkとすると、10進数と2進数はそれぞれつぎのように表される。
- 10進数
-
nk×10k-1+...+n2×101+n1×100
- 2進数
nk×2k-1+...+n2×21+n1×20
2進法では少し数が大きくなると、桁数がたちまち増える。人間の目には煩わしい。しかし、数字は1と0しかないので、四則演算もふたつの数字の4つの組合わせさえ考えれば足りる。単純な演算を大量に扱うのは、コンピュータのもっとも得意とするところだ。この2進数の演算をどのような場合にどう用いればよいのかご説明したい。
ActionScript 3.0定義済みクラスで使われている2進数の考え方
ActionScript 3.0定義済みクラスで2進数の考え方が使われている例をひとつ紹介しよう。それは、Arrayクラスだ。第24回「インスタンスの管理と配列の並べ替え」の「インスタンスの重ね順を管理する」で、Array.sort()メソッドに渡せるArrayクラスの定数を掲げた(第24回表2再掲)。
表2 Array.sort()メソッドに指定できるArrayクラスの定数(再掲)
| 定数 | 説明 |
|---|
| CASEINSENSITIVE | 英字の大文字小文字を区別せずに並べ替える。 |
|---|
| DESCENDING | 並べ替えの順序を、降順(大きい順)に指定する。 |
|---|
| NUMERIC | エレメントが数値の配列を、その値の大きさで順序づける。 |
|---|
| RETURNINDEXEDARRAY | ターゲットの配列は変更せず、並べ替えた結果の整数インデックスをエレメントとした配列が返される。 |
|---|
| UNIQUESORT | エレメントに重複がない配列のみを並べ替える。重複があれば、0を返す。 |
|---|
これらの定数には整数値が与えられている。たとえば、定数Array.NUMERICの数値は16で、Array.DESCENDINGは2だ。すると、これらふたつの合計値Array.NUMERIC+Array.DESCENDING(18)をArray.sort()メソッドの引数に渡すと、配列エレメントが数値の大きい順に並べ替えられる。
var my_array:Array = [30, 0, 1000, 4, 200];
my_array.sort(Array.NUMERIC + Array.DESCENDING);
trace(my_array); // 出力: 1000,200,30,4,0
こういう結果が得られるのは、18という値は定数Array.NUMERICとArray.DESCENDINGの組合わせ以外ありえないからだ。さらにいえば、これらArray定数のどの組合わせの合計をとっても一意、つまり他の組合わせの合計にはならない。Array定数値はそのように定められている。
種明かしは簡単で、定数値を2進数で見ればよい(表1)。各定数値は、先頭が1で後は0の2進数だ。そしてみな桁数が異なる。すると、10進数の18は2進数では10010となり、1の桁がふたつあることからふたつの定数の組合わせになる。そして、1の桁の位でふたつがどの定数かもわかる。
表1 Arrayクラスの定数と与えられた整数値
| Arrayクラスの定数 | ソートの指定 | 与えられた10進数 | 2進数表現 |
|---|
| CASEINSENSITIVE | 大文字小文字を区別しない | 1=20 | 1 |
|---|
| DESCENDING | 降順値(大きい順)の並べ替え | 2=21 | 10 |
|---|
| UNIQUESORT | 重複のない並べ替え | 4=22 | 100 |
|---|
| RETURNINDEXEDARRAY | 並べ替えたインデックスの配列を返す | 8=23 | 1000 |
|---|
| NUMERIC | 数値の大きさで並べ替え | 16=24 | 10000 |
|---|
ビット単位の論理和演算
[ヘルプ]でArray.sort()メソッドを調べると、引数に定数を「複数指定する場合は、ビット単位の論理和(OR)|演算子で区切」るとしている。使うのは加算演算子+ではないというのだ。しかし、少なくともArray定数については、結果はビット単位の論理和Iでも加算+でも変わらない。異なるのは演算の対象となる桁同士が、どちらも1のときだ[1]。
1+1=10(2進数)
1|1=1(2進数)
加算の場合にはひと桁繰り上がる。だが、「ビット単位の演算」では、計算した桁同士の結果が他の桁に影響を及ぼすことはない。つまり、繰り上がりや繰り下がりは起こらない(表2)。もっとも、Array定数についていえば、そもそも1のある桁はすべての定数で異なるように定められている。だから繰り上がりはなく、加算でも結果は変わらない。
表2 ビット単位の論理和演算子|の演算結果
| ビット単位の論理和演算 | 結果の2進数 |
|---|
| 0|0 | 0 |
0|1
1|0 | 1 |
| 1|1 | 1 |
とはいえ、繰り上がり・繰り下がりのない計算とある計算でどちらが楽かを考えれば、ビット演算に軍配は上がる。したがって、最適化を目指すなら、ビット単位の演算をできるだけ使った方がよい。ちなみに、「ビット」というのは2進数のひと桁を示す。ビット単位の演算というのは、2進数を桁ごとに計算するということだ。
前述のとおり、2進法の演算は1と0の4とおりの組合わせしかないので、結果については問題なかろう(前掲表2)。しかし、2進数とその計算をどういうときに用いるのか、具体的な例が思い浮かばないかもしれない。そこで、ごく簡単なゲームの中で、2進数とビット単位の演算を使ってみよう。
複数フラグを配列で扱う
ゲームの内容はつぎのとおりだ。まず、4つのインスタンスを同じ向きで並べる(図1上段)。つぎに、ボタンをクリックすると、その中のランダムなひとつの向きが逆になる(図1中段)。そして、ボタンクリックを繰返し、すべてのインスタンスの向きが初めと逆になれば上がりとする(図1下段)。
図1 ボタンでランダムにひとつのインスタンスを反転する
初めはみんな右向き
 ボタンでランダムなひとつの向きが逆転
ボタンでランダムなひとつの向きが逆転
 すべてが左を向くと上がり
すべてが左を向くと上がり
先に、2進数を使わないやり方を考えよう。初めのインスタンスを裏向きとして、クリックするたびに逆転する。ゲームを進めるうえで、そのときどきの向きをインスタンス4つ分つねにもっておかなければならない。このようなとき、インスタンスの向きはブール(論理)値として、4つの値を配列に納めるのが定石といえる。
オン/オフあるいはYes/Noのような2値の状態を示す変数は「フラグ」と呼ばれる。つまり、今回の考え方はインスタンス4つの向きをフラグにして、配列に入れて扱うということだ[2]。初めの向きをfalseとしておこう。
var flag:Array = [false, false, false, false];
配列のエレメント4つからランダムなひとつのブール値を反転するには、つぎのようなスクリプトを書けばよいだろう。論理否定演算子!は、ブール値のtrueとfalseを反転する。
var nLength:uint = 4;
var nRandom:uint = uint(Math.random() * nLength);
flag[nRandom] = !flag[nRandom];
上がり、つまりすべてのフラグがtrueになったかどうかは、関数(xAllOn())を定義して確かめることにする。フラグの配列(flag)からforループで取出したエレメントの値を順に調べる。そして、falseの値が見つかったら、returnステートメントで直ちに関数から抜けて戻り値falseを返した。これで無駄な繰返しが避けられる。途中で抜けることなくループ処理が済んだとき、エレメントすべてがtrueだったことを意味するので、戻り値としてtrueを返している。
function xAllOn():Boolean {
for (var i:uint = 0; i < nLength; i++) {
if (flag[i] == false) {
return false;
}
}
return true;
}
このようにフラグを配列に入れる考え方は、実際によく使われる。このゲームくらいの内容であれば、最適化の具体的な問題も生じないだろう。しかし、2進数とビット単位の論理演算を使うと、慣れないと見た目わかりづらいものの、スクリプトそのものはかなりすっきりする。
なお、ゲームにおけるインスタンスのアニメーションやボタンのスクリプトなどは、今回の本題ではないので省く。ダウンロードサンプルには加えておくので、興味がある読者はそちらをご覧いただきたい。
2進数の各桁をフラグとして扱う
2進数の各桁の数字は1か0だ。したがって、ひとつひとつの桁をフラグとして捉えることができる。4つのインスタンスの初めの向きを2進数4桁の0000と考えれば、10進数の(もちろん2進数でも)0になる。すると、上がりは2進数1111となり、10進数では15だ。
var flag:uint = 0; // 2進数0000
var end:uint = 15; // 2進数1111
2進数のある桁の1と0を入替えるには、ビット単位の排他的論理和演算子^を使う。演算結果は次表3のとおりだ。論理和演算子|と同じく、上から3つの組合わせは加算演算子+と変わらない。1同士の演算をしたとき、排他的論理和は0になる。
表3 ビット単位の排他的論理和演算子^の演算結果
| ビット単位の論理和演算 | 結果の2進数 |
|---|
| 0^0 | 0 |
0^1
1^0 | 1 |
| 1^1 | 0 |
表3の演算の組合わせから^演算子の右側が1の場合(2番目と4番目)を取出すと、演算結果はつぎのように左側の1と0が反転している。つまり、2進数のある桁の1と0をひっくり返すには、1との排他的論理和をとればよい。
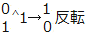
後は、1をもつ2進数の桁の変え方だ。これには、ビット単位の左シフト<<という、まさに桁をずらすための演算子がある[3]。たとえば、1<<2で1の後に0がふたつついた2進数100(10進数4)になる。
2進数として扱う数<<左にずらす桁数
これで4桁の2進数のランダムなひと桁を反転させることができる。スクリプトはつぎのようになる。
var nLength:uint = 4;
var nRandom:uint = uint(Math.random() * nLength);
flag ^= (1 << nRandom);
そして、このお題の目玉は4つのフラグすべてが反転したかどうかを確かめる関数(xAllOn())だ。配列に入れたフラグすべてを調べる前項の場合と比べて、あっけないほど簡単だ。4桁の2進数が1111、つまり10進数の15と等しいかどうか比べれば済む。
function xAllOn():Boolean {
return (flag == end);
}
以上の2進数のビット演算を組合わせて、簡単なテスト用スクリプトを書いてみよう。タイムラインにインスタンスは置かない。ステージをクリックするたびに、4桁の2進数のうちのひと桁がランダムに反転して、[出力]パネルに表示される(図2)。1111が表示されれば上がりだ。
図2 4桁の2進数のうちのひと桁がランダムに反転する
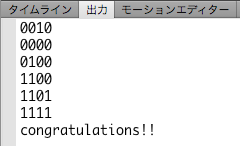
StageオブジェクトのInteractiveObject.clickイベント(定数MouseEvent.CLICK)にリスナー関数(xRandomReverse())を加え、2進数のランダムなひと桁を反転させるようにしたのが以下のスクリプト001だ。フラグを確かめる関数(xAllOn())で上がりとされたら、"congratulations!!"の文字を[出力]してリスナー関数を除いている。
スクリプト1 ステージをクリックするたびに4桁の2進数のうちのひと桁がランダムに反転する
// フレームアクション: メインタイムライン
var flag:uint = 0; // 2進数0000
var end:uint = 15; // 2進数1111
var nLength:uint = 4;
stage.addEventListener(MouseEvent.CLICK, xRandomReverse);
function xRandomReverse(eventObject:MouseEvent):void {
var nRandom:uint = uint(Math.random() * nLength);
flag ^= (1 << nRandom);
trace(("000" + flag.toString(2)).substr(-nLength));
if (xAllOn()) {
trace("congratulations!!");
stage.removeEventListener(MouseEvent.CLICK, xRandomReverse);
}
}
function xAllOn():Boolean {
return (flag == end);
}
uint.toString()メソッドは、整数(uint)を文字列に換える。そのとき、引数に基数として2を渡すと、数字は2進数で表される。String.substr()メソッドは、String.substring()と同じく[4]、文字列から一部の文字を取出す。ただ、ふたつのメソッドは引数の定めが異なる。
文字列.substr(開始インデックス, 文字数)
第2引数は、終了インデックスではなく、文字数となる。これを省けば最後の文字までとみなされる。もうひとつ、String.substring()メソッドと違うのは、第1引数に負数が渡せ、文字列の最後からインデックスが数えられる。つまり、前掲スクリプト001のように-4(nLength)を渡すと、下4桁が取出せるのだ。
インスタンスのアニメーションやButtonコンポーネントを加えたサンプルは、参考までにダウンロードファイルに加えておくので、関心のある読者はそれをご覧いただきたい(前掲図1参照)。
さて、これで拙著『ActionScript 3.0パフォーマンスチューニング』の紹介を兼ねた特別編を終える。興味をもたれた方は書店で手にとってご覧いただくか、筆者の書籍紹介サイトにChapter01をPDFプレビューとして公開しているのでお読みいただきたい。
今回解説した次のサンプルファイルがダウンロードできます。