まだ挑戦していない方は、ぜひ先を読み進める前に挑戦してみてください。
キーワードは「ユークリッドの互除法」と「フィボナッチ数列」
今回の問題では、「コンパスとハサミを使って、長方形をチョキチョキと切る」というルールが与えられています。そのルールに注意しつつ、「ハサミを使う回数をできるだけ少なくするような長方形を求めなさい」という問題ですね。
このルールがいったい何を意味しているのかを見抜くことが、問題を解くうえで重要になってきます。
今回のハサミ問題のキーワードは、2つあります。
1つは「ユークリッドの互除法」。
もう1つは「フィボナッチ数列」です。
ユークリッドの互除法の代わりに「互いに素」や「最大公約数」がキーワードだと思ってもよいでしょう。
コンパスとハサミの操作は「ユークリッドの互除法」になっている
「ユークリッドの互除法」は、2つの正の整数が与えられた時、その最大公約数を求めるアルゴリズムです。アルゴリズムを学ぶほとんどの人が最初に学ぶアルゴリズムであるうえ、“世界で最古のアルゴリズム”といってよい歴史的なものです。
ユークリッドの互除法は、以下のようなアルゴリズムです。
図1 ユークリッドの互除法(入力と出力)
 図2 ユークリッドの互除法(手続き)
図2 ユークリッドの互除法(手続き)

じつは、今回の問題の「コンパスとハサミを使った操作」は、ユークリッドの互除法そのものなのです。長方形の縦と横を「与えられた正の整数」だとし、問題文に与えられている操作を行っていくと、ハサミを使わずに終わった「最後の長方形」の短辺は、最大公約数になるのです。「コンパスとハサミを使う」という図形的な操作で最大公約数が求められるというのは、おもしろいですね。
なぜ、コンパスとハサミの操作がユークリッドの互除法になっているかを、くわしく見ていきましょう。
長方形Aの長辺をmとし、短辺をnとします。短辺nを半径にして、コンパスで四分の一円を描けるだけ描き、最後に長方形Bが残ったとします。
そのとき、残った長方形Bの短辺はどうなるかというと、長方形Aの長辺mを短辺nで割ったときの「余り(m mod n)」に相当します。
ですから、コンパスとハサミの操作というのは、
- (長辺, 短辺)=(m, n)の長方形から
- (長辺, 短辺)=(n, m mod n)の長方形を得る
操作になります。
これを、長辺がちょうど短辺の倍数になるまで繰り返すのですが、これはまさにユークリッドの互除法にほかなりません。今回の問題でいう「ハサミの回数」は、「余りを求める回数(割り算の回数)」に相当します。
ここまでは、アルゴリズムを学んだことのあるプログラマならばよく理解できるはずです。
しかし、ここまでの理解だけで、今回のハサミ問題を解くのは難しいでしょう。というのは、適当な長方形を作って試しても、なかなか40回という数にまで至らず、意外と少ない回数で操作が終了してしまうのです。
言い換えればこれは、ユークリッドの互除法は「非常に効率のよいアルゴリズム」ということでもあります。ハサミの回数が少ないということは、割り算の回数が少なくてすむということになるからです。
「ハサミ40回」の逆から考えるのがポイント
じつは、今回の問題を解くためには、ユークリッドの互除法を使う必要はまったくありません(!)。
今回の問題を解くときには、最初から「ハサミ40回」に挑戦するのではなく、少ない回数から考えるのがポイントです。つまり逆に考えるということです。
短辺が1のとき、どんな長方形でもハサミ0回で終了します。
短辺が2のとき、長辺が3の長方形のときハサミ1回で終了します。つまり、ハサミ1回の最小長方形(a)は、2×3です。
短辺が3のとき、コンパスを1回だけ使って、残りの長方形がさっきの(a)になるようにすれば、ハサミ2回の最小長方形(b)が作れます。長辺を3+2=5にすればいいということです。つまり、ハサミ2回の最小長方形(b)は、3×5です。
ということは、ハサミ40回の最小長方形を作るためには
- 「コンパス1回だけ使って切り取った残りの長方形が、一歩手前の最小長方形になるような長方形を作る」
操作を繰り返していけばいいと予想できます。
それは言い換えると
- 「長辺が次の短辺になり、長辺と短辺の和が次の長辺になるような長方形を作る」
という操作の繰り返しです。言葉で説明するとわかりにくいですが、これは次の図のような「らせん」を描くことに相当します。
図3 長方形が作り出すらせん
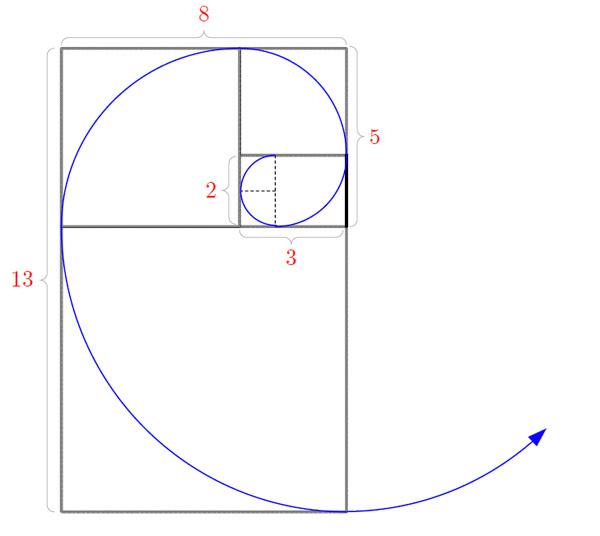
じつは、このような操作は「フィボナッチ数列」を作り出していることにほかなりません。これが今回の問題の2つ目のキーワードです。
フィボナッチ数列を作り出せば正解が見える
フィボナッチ数列というのは、以下の漸化式で定義された数列です。
F[1] = 1
F[2] = 1
F[k] = F[k-2] + F[k-1]
(k = 3,4,5,...)
具体的には、フィボナッチ数列は、以下の数列になります。
1, 1, 2, 3, 5, 8, 13, ...
図4 フィボナッチ数列の計算(入力と出力)
 図5 フィボナッチ数列の計算(手続き)
図5 フィボナッチ数列の計算(手続き)

- ハサミ1回の最小長方形は2×3。これは、(短辺, 長辺) = (F[3], F[4])に相当します。
- ハサミ2回の最小長方形は3×5。これは、(短辺, 長辺) = (F[4], F[5])に相当します。
つまり、今回の問題を解くためには「フィボナッチ数列を作り出していけばいい」ということになります。以下、ハサミn回を使う長方形を列挙してみます。
| ハサミ1回 | 2×3 |
|---|
| ハサミ2回 | 3×5 |
|---|
| ハサミ3回 | 5×8 |
|---|
| ハサミ4回 | 8×13 |
|---|
| ハサミ5回 | 13×21 |
|---|
| ハサミ6回 | 21×34 |
|---|
| ハサミ7回 | 34×55 |
|---|
| ハサミ8回 | 55×89 |
|---|
| … |
| ハサミ39回 | 165580141×267914296 |
|---|
| ハサミ40回 | 267914296×433494437 |
|---|
よって、正解は以下になります。
267914296x433494437
この解答が最小面積になることは、数学的にも証明できます。
挑戦者の解答結果は
今回のハサミ問題は、挑戦受付人数128人に設定しましたが、挑戦開始後わずか2日間で受付人数をオーバーしてしまいました。たくさんの方の挑戦、ありがとうございました。
評価分布
| 評価5 | 98名 |
|---|
| 評価3 | 14名 |
|---|
| 評価1 | 16名 |
|---|
| 合計 | 128名 |
|---|
評価基準
1人が複数回投稿した場合には、最終投稿のみを評価しました。評価基準は以下のとおりです。
- 評価5⇒ ぴったり正解(小数による解答も判断の上含めました)
- 評価3⇒ 形式上のミスはあったが、内容は正解と判断(最小面積でなくても40回ならこちら)
- 評価1⇒ 残念ながら不正解(ハサミの回数1回ずれはこちら)
挑戦者には個別に評価フィードバックを送りましたが、その中で1点おわびをしました。ハサミ問題の公開時点では「長さは正の整数とする」という条件を入れていなかったからです(公開当日に修正)。面積が小さい方が高い得点と指示したこともあり、どう考えればよいか迷った挑戦者もおり、中には小数で解答した方もいらっしゃいました。
解答を吟味のうえ、長方形の辺の長さが小数になっているものは、ハサミの回数が正確に40回になっていれば評価5としました。
長方形の辺の長さが整数の場合、ハサミの回数が正確に40回になっていても、面積が最小でないならば評価3としました。たとえば、1746860020068409x4217293152016490は、ハサミの回数は正確に40回になりますが、面積が大きいため、評価3です。
たいへん惜しくも「ハサミの回数1回ずれ」の解答がいくつかありました。つまり、165580141x267914296にしてしまった方ですね。これだとハサミの回数は39回になってしまいます。今回は評価1としました。このような「1回ずれ」は、オフ・バイ・ワン(off-by-one)のエラーなどと呼ばれることもあり、プログラミングではよくあるミスなので、厳しく採点しました。
その一方で、267914296x433494437を433494437x267914296と逆に書いた解答もありました。問題の指示では「縦x横」の形式で「縦≦横」でなければならなかったのですが、こちらは評価3としました。
解答あれこれ
多くの解答者が、今回の2つのキーワード(ユークリッドの互除法・フィボナッチ数列)をメッセージ中に書いていました。
これらのキーワードに気づいたタイミングは、人それぞれです。問題を見た瞬間に気づく、具体例を作っているうちに気づく、プログラムを書いている途中で気づく、プログラムを動かして気づく……などですね。これらのキーワードにはまったく気づかずに正解している方もいらっしゃいました(もちろん、その方も文句なく正解です)。
解答者が使ったプログラミング言語やソフトウェアは、以下のように多彩でした(もしも抜けがあったらごめんなさい)。
C, C#, C++, Clojure, Common Lisp, Excel, Groovy, Haskell, Java, Objective-C, Pascal, Perl, PHP, Processing, Python, Ruby, Scala, Scheme, VBA...
最後に
以上が「ハサミ問題」です。楽しんでいただけたでしょうか。
結城はこれからもCodeIQで出題していきますので、次回もぜひチャレンジしてくださいね。挑戦ありがとうございました!
- CodeIQ
- URL:http://www.hyuki.com/codeiq/
参考プログラム
参考まで、結城が用意した解答を作りだすプログラム(list_scissors.pl)は以下です(Perl)。
リスト1 list_scissors.pl
# list_scissors.pl
use strict;
use warnings;
# F_1=1, F_2=1, F_3=2, F_4=3, F_5=5, F_6=8, ...
# ハサミを1回使う最小の長方形は、2x3のとき(1x2が「端」になる)。
# ハサミを2回使う最小の長方形は、3x5のとき(2x3が「端」になる)。
# ハサミを3回使う最小の長方形は、5x8のとき(3x5が「端」になる)。
# …
# ハサミをn回使う最小の長方形は、F_{n+2} x F_{n+3}のとき(F_{n+1} x F_{n+2}が「端」になる)。
my $height = 2;
my $width = 3;
my $n = 40;
for (my $k = 1; $k
また、解答チェックのために作った、与えられた長方形が何回ハサミを使うことになるかを調べるプログラム(try_scissors.pl)は以下です。何個かサンプルも付けました(解答のすべてではありません)。
リスト2 try_scissors.pl
# try_scissors.pl
use strict;
use warnings;
sub scissors {
my ($m, $n) = @_;
print "scissors($m, $n) = ";
my $count = 0;
if ($m
実行結果は以下です。
scissors(42, 144) = 2
scissors(267914296, 433494437) = 40
scissors(1746860020068409, 4217293152016490) = 40
scissors(1746860020068409, 2470433131948081) = 40
scissors(165580141, 267914296) = 39








