はじめに
今回からは、
今回は線分を表すクラスを作成し、
線分クラス
では早速、
public class LineSegment {
public double x1;
public double y1;
public double x2;
public double y2;
public LineSegment(double x1, double y1, double x2, double y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
@Override
public String toString() {
return "(" + x1 + ", " + y1 + ") - (" + x2 + ", " + y2 + ")";
}
}さて、
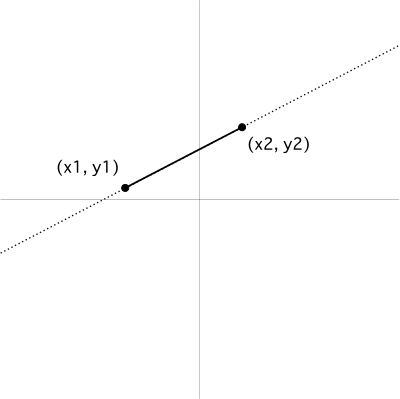
public Line toLine() {
return Line.fromPoints(x1, y1, x2, y2);
}線分と直線の交差判定
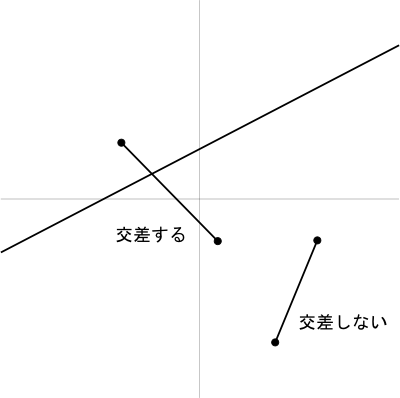
2つの直線は、
なお、
以下の直線の方程式を考えます。
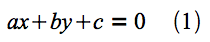
この式の等号を不等号に変えることで、
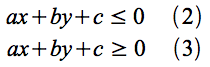
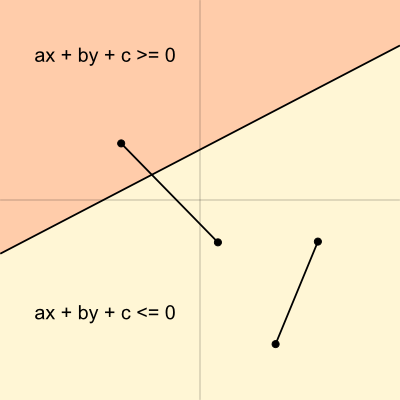
図4を見ると、
これを実装してみましょう。LineSegmentクラスに、
public boolean intersects(Line l) {
double t1 = l.a * x1 + l.b * y1 + l.c; // 端点1の座標を直線の式に代入
double t2 = l.a * x2 + l.b * y2 + l.c; // 端点2の座標を直線の式に代入
return (t1 = 0) || (t1 >= 0 && t2 上のコードの不等式判定は、
public boolean intersects(Line l) {
double t1 = l.a * x1 + l.b * y1 + l.c;
double t2 = l.a * x2 + l.b * y2 + l.c;
return t1 * t2 線分同士の交差判定
- ※
- 以下で解説しているアルゴリズムには、
特別な状況で正しく動作しない問題がありました。詳細は 「第7回 (臨時回) 線分の交差判定再訪 )」を参照してください。
次に、
図5のように、
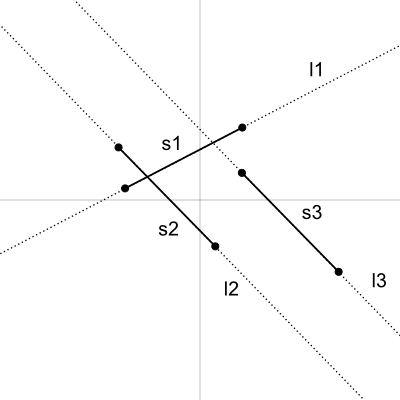
一方、
以上を踏まえて、
public boolean intersects(LineSegment s) {
return intersects(s.toLine()) && s.intersects(toLine());
}線分と直線、線分同士の交点座標
線分と直線、
この方針に基づいて、
public Point2D getIntersectionPoint(Line l) {
if (!intersects(l)) {
return null; // 交差しない場合はnullを返す
}
return l.getIntersectionPoint(toLine());
}
public Point2D getIntersectionPoint(LineSegment s) {
if (!intersects(s)) {
return null; // 交差しない場合はnullを返す
}
return s.toLine().getIntersectionPoint(toLine());
}動作確認
今回実装した線分の交差判定をグラフィカルに動作確認できるよう、
デモプログラムを起動すると、
まとめと次回予告
今回は、
今回作成したプログラムとデモ用のSwingアプリケーションのソースコードは、
今回作成したプログラムのソースコードがダウンロードできます。
- 第2回ソースコードファイル
(gihyo-geometry-part2. zip/ Zip圧縮/約15KB)
次回からは、



