はじめに

今回は、平面走査法による線分交差検出のデータ構造を実装していきます。内容がかなり難しくなってきますが、説明とソースコードを納得できるまで読み返していただければと思います。

平面走査法と水平方向

前回は、多数の線分から交差を検出する方法として、平面走査法（plane sweep algorithm）の考え方を紹介しました。これは、x軸に平行な走査線を上から下へと動かしていき、走査線と交わる線分のみを計算対象とすることで、交差検出の計算量を減らすというものでした（図1⁠）⁠。

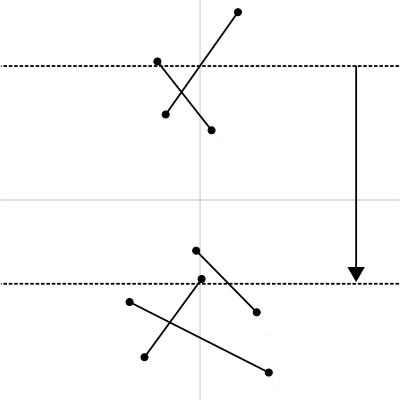
実は、これだけでは考え方としてまだ不足なのです。図2を見てください。図2では図1と違い、すべての線分が同じくらいのy座標範囲にまとまって存在しています。こうした場合、走査線が多数の線分と交わる時間が大半を占めるため、計算量をほとんど削減できないことになってしまいます。

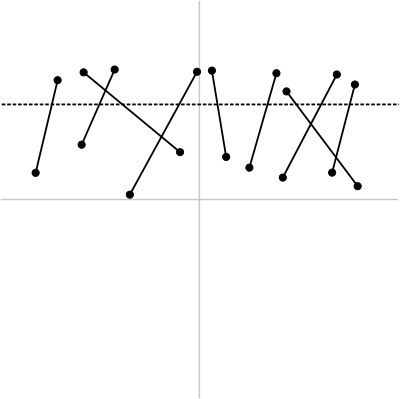
この状況を改善するには、走査線で垂直方向の計算範囲を限定することに加えて、水平方向にも計算の局所性を持たせる必要があります。具体的には、走査線と線分の交点のx座標を基準にして、水平方向に隣接した線分同士の交差のみをチェックするのです。この様子を図3に示します。

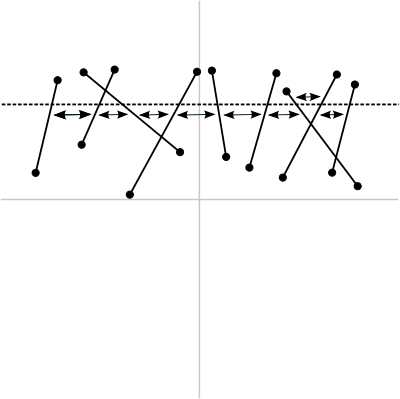
平面走査法のデータ構造

以上が、平面走査法による線分交差検出の概要です。このアルゴリズムを実装していくわけですが、まず初めに、アルゴリズムで用いるデータ構造を3つ導入します。3つのデータ構造とは、イベント、イベントキュー、そしてステータスです。

なお、今回からは図4のように、y座標が上から下に向かって増加する座標系を採用します。

イベント

走査線は上から下まで動かすと先に述べました。しかし、実際のアルゴリズムでは連続的に動かすわけではなく、特定のイベント点を単位として、離散的に位置を変化させることになります。

イベント点になるのは、アルゴリズムの入力となるすべての線分の端点、そして、計算途中で検出された線分同士の交点です。計算の開始時点では、線分の端点に対応するイベントのみが存在しますが、走査線が移動し、新たな交点が見つかるたびに、交点に対応するイベントが生成されていきます。

イベントオブジェクトは、そのイベント点の座標と、点の種類（線分の始点、線分の終点、線分同士の交点のいずれか）を保持します。さらに、点に関連する線分（始点または終点イベントの場合はその線分、交点イベントの場合は交差する2線分）も合わせて保持します。

イベントキュー

イベントキューは、イベントの順序付き集合です。ここでの順序は、イベントのy座標の大小関係にもとづいて定義され、イベントキューの先頭位置にあるイベントはキューの中で最小のy座標を持ちます。走査線を現在の位置から次の位置へと移動する処理は、イベントキューから先頭のイベントを取り出す作業に相当します。

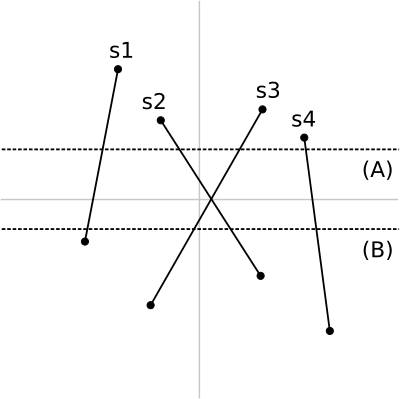
ステータス

ステータスは、現在の走査線と交差するすべての線分の順序付き集合です。ここでの順序は、走査線と各線分の交点のx座標の大小関係にもとづいて定義されます。この順序関係は、走査線の移動にともなって動的に変化します。例えば、図5で走査線が(A)の位置にあるとき、ステータスは(s1, s2, s3, s4)の順序を保持していますが、走査線が(B)まで下がると、順序は(s1, s3, s2, s4)に変化します。

順序付き集合：TreeSetクラス

イベントキューとステータスのところで、順序付き集合という言葉が出てきました。順序付き集合とは、特定の順序関係にしたがって、要素が常にソートされている集合です。Javaでこの要請をみたすクラスは、java.util.TreeSetです。TreeSetは、赤黒木（red-black tree）と呼ばれる平衡二分木で実装されており、以下のようなメソッドが利用できます。

・add(element)

集合にelementを追加します。

・remove(element)

集合からelementを削除します。

・pollFirst() - Java 6以降

先頭（最小）の要素を取得し、その要素を集合から削除します。集合が空の場合はnullを返します。

・lower(element) - Java 6以降

elementよりも小さい要素のうち、最大のものを返します。elementよりも小さい要素が存在しない場合はnullを返します。

・higher(element) - Java 6以降

elementよりも大きい要素のうち、最小のものを返します。elementよりも大きい要素が存在しない場合はnullを返します。

TreeSetクラスの非常に重要な特徴は、上記のメソッドすべてがlog(n)時間で実行できることです。本連載では、イベントキューとステータスの両方にTreeSetを使用します。TreeSetの詳細は、こちらのAPIドキュメントを参照してください。

イベントクラス

それでは、イベントクラスを用意しましょう。Eventクラスは、Comparableインターフェースを実装することで、イベントキューに格納するときの順序関係（y座標順）を定義します。

public class Event implements Comparable<Event> {
    public enum Type { // イベントの種類
        SEGMENT_START, // 線分の始点
        SEGMENT_END,   // 線分の終点
        INTERSECTION   // 線分同士の交差
    }

    public Type type;
    public double x;
    public double y;
    // 点に関連する線分1
    public LineSegment segment1;
    // 点に関連する線分2（type = INTERSECTIONのときのみ使用）
    public LineSegment segment2;

    public Event(Type type, double x, double y, LineSegment segment1,
            LineSegment segment2) {
        this.type = type;
        this.x = x;
        this.y = y;
        this.segment1 = segment1;
        this.segment2 = segment2;
    }

    // Comparable<Event>>の実装
    public int compareTo(Event e) {
        int c = Double.compare(y, e.y); // イベント点のy座標を比較
        if (c == 0) { // y座標が等しい場合はx座標を比較
            c = Double.compare(x, e.x);
        }
        return c;
    }
}

走査線ベースの線分コンパレータ

次に、ステータスで必要となる、走査線と線分の交点のx座標にもとづく順序の比較を、SweepLineBasedComparatorクラスとして作成しましょう。これは、Comparatorインターフェースを実装したコンパレータ（比較子）になります。

SweepLineBasedComparatorクラスを作成するときに注意が必要なのは、2つ以上の線分が走査線の位置でちょうど交差するとき、どう順序を付けるかです。この場合、走査線の下に伸びた線分を見て、より左に位置する方の線分が小さいものとします。

以上のルールを実装したものが、次のコードになります。

public class SweepLineBasedComparator implements Comparator<LineSegment> {
    private Line sweepLine;
    private Line belowLine;

    public SweepLineBasedComparator() {
        setY(0);
    }

    // 走査線のy座標を更新
    public void setY(double y) {
        // 走査線を更新
        sweepLine = Line.fromPoints(0, y, 1, y);
        // 走査線の少し下を通る線を作成
        belowLine = Line.fromPoints(0, y + 0.1, 1, y + 0.1);
    }

    // Comparator<LineSegment>の実装
    public int compare(LineSegment s1, LineSegment s2) {
        int c = compareByLine(s1, s2, sweepLine);
        if (c == 0) { // 走査線上の交点が等しい場合は、走査線の少し下の位置で比較
            c = compareByLine(s1, s2, belowLine);
        }
        return c;
    }

    // s1とs2を、lineとの交点のx座標にもとづいて比較
    private int compareByLine(LineSegment s1, LineSegment s2, Line line) {
        Point2D p1 = s1.toLine().getIntersectionPoint(line);
        Point2D p2 = s2.toLine().getIntersectionPoint(line);
        // 交点がnull（線分とlineが平行）の場合は線分の1端点を比較値に採用
        double x1 = p1 != null ? p1.getX() : s1.x1;
        double x2 = p2 != null ? p2.getX() : s2.x1;
        return Double.compare(x1, x2);
    }
}

上のコードで、compareByLine()メソッドに走査線と平行な線分が渡された場合、走査線と線分の交点が存在しないため、比較用のx座標が得られません（p1またはp2がnullになる⁠）⁠。この場合は、代用の値として線分の1端点のx座標（LineSegment#x1）を使用しています。

まとめと次回予告

今回は、平面走査法による線分の交差検出の詳細を解説し、イベント、イベントキュー、ステータスの3つのデータ構造を導入しました。また、イベントキューとステータスに使用する順序付き集合としてTreeSetクラスを説明しました。さらに、ステータス上の順序関係を定義する線分のコンパレータも作成しました。

次回は、今回のデータ構造を土台として、平面走査法のアルゴリズムを実装します。お楽しみに！