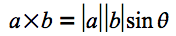はじめに
前々回は凸多角形を取り上げましたが、今回はその凸多角形に対する演算として、点の包含判定方法と面積の計算方法を学習します。
Blogopolisにおける多角形の点包含判定と面積計算
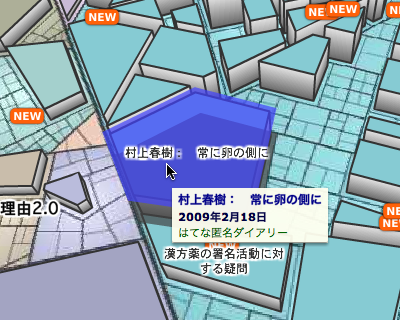
Blogopolisでは、多角形の土地にマウスカーソルを合わせると、その土地がハイライト表示され、さらにクリックすることで土地の詳細情報が表示されるようになっています(図1)。内部的には、マウスカーソルが移動するたびに、その座標が画面上の各多角形の内部にあるか、外部にあるかを判定しているわけです。
図1 Blogopolisにおけるマウスヒット領域のハイライト
また、Blogopolisでは、1つ1つのブログ記事を表す土地の面積が、その記事へのはてなブックマーク数に応じて決められており、多くのブックマークを集めた記事ほど大きな土地を獲得するようになっています。これは内部的には、土地の区画を生成する過程で、各多角形の面積を計算しながら、適切な面積比になるような調整を行っているわけです。
こうした「点の包含判定」や「面積の計算」といった演算は、長方形や円に対して行うのであれば非常に簡単です。しかし、Blogopolisのような多角形の場合、どうすれば良いのでしょうか。
多角形の点包含判定
まず、凸多角形の点包含判定問題を考えます。これは、与えられた点(x, y)が、凸多角形の内部にあるか、それとも外部にあるかを調べるものです。
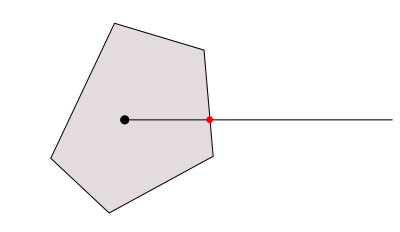
点(x, y)を始点とし、右水平方向に永遠に延びる半直線(half-line)を考えます。もし、点が凸多角形の内部に存在するのであれば、この半直線は、多角形の「境界から脱出する」ために、多角形が持ついずれかの辺と、必ず1回交差します(図2)。
図2 多角形が包含する点と半直線の交差
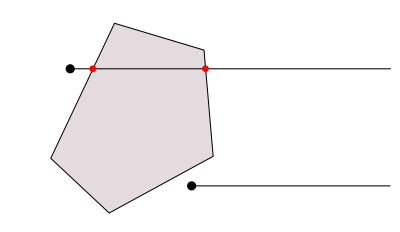
一方、点が凸多角形の外部に存在するのであれば、半直線は多角形の辺とはまったく交差しないか、一度多角形の内部に「突入」してから「突き抜ける」かたちになります。つまり、半直線と辺の交差回数は、0回または2回になります(図3)。
図3 多角形が包含しない点と半直線の交差
このように、凸多角形に対しては、半直線と辺の交差回数が1回であれば点を包含しており、0回か2回であれば包含していないと判断することができます。
なお、以上の判定条件は、凸でない多角形についても一般化が可能です。一般の多角形に対しては、半直線と辺の交差回数が奇数であれば点を包含しており、偶数であれば包含していないと判断できます。
この方針にしたがい、前回作成したConvexPolygonクラスに、半直線と辺の交差回数の偶奇から点の包含を判定するcontains()メソッドを記述してみましょう。ここで問題となるのは、半直線のクラスを本連載では作成していないことです。しかし、十分な長さを持つLineSegmentオブジェクトを用意すれば、これは擬似的に半直線と見なすことができますので、今回はLineSegmentオブジェクトを半直線の代用とすることにします。
リスト contains()メソッドの記述(Java)
public boolean contains(double x, double y) {
// 多角形のy座標範囲を求める
double minY = Double.POSITIVE_INFINITY;
double maxY = Double.NEGATIVE_INFINITY;
for (Point2D v : vertices) {
minY = Math.min(minY, v.getY());
maxY = Math.max(maxY, v.getY());
}
// yが最小値-最大値の範囲外の場合はfalseを返す
if (y <= minY || y >= maxY) {
return false;
}
// 与えられた座標を始点とし、右方向に十分長く延びる擬似的な半直線を作成
LineSegment halfLine = new LineSegment(x, y, x + 10000000, y);
int count = 0;
for (LineSegment edge : edges) {
// 半直線が辺の終点とちょうど重なる場合、次の辺の始点とも交差が検出され、
// 二重にカウントされてしまうため、カウントをスキップする
if (edge.y2 == y) {
continue;
}
if (edge.intersects(halfLine)) {
count++;
}
}
// 交差回数が奇数の場合は点を包含
return count % 2 == 1;
}
上のコードでは、初めに多角形のy座標範囲を求めた後、渡された点のy座標がその範囲にない場合は、交差回数をチェックせずにfalseを返すようにしています。このようにしないと、点のy座標が多角形の一番上の頂点または一番下の頂点のy座標と一致する場合に、正しい判定が行われない可能性があります(なぜか考えてみてください)。
念のため再度述べますが、この点包含判定のアルゴリズムは、凸でない多角形にも適用できます。
多角形の面積計算
続いて、凸多角形の面積を計算する方法を考えてみましょう。面積と聞いて、前々回の内容から、何か思い出すことがないでしょうか。そう、外積です。2つのベクトルの外積は、そのベクトルが作る平行四辺形の符号付き面積に等しくなるのでした。外積の式と図を以下に再掲します。
式1 平面幾何におけるベクトルの外積
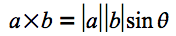 図4 平行四辺形の符号付き面積
図4 平行四辺形の符号付き面積
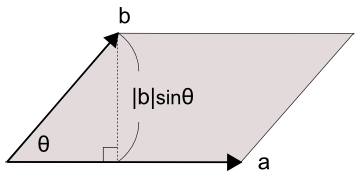
この外積をうまく利用すれば、凸多角形の面積計算ができそうです。話を簡単にするために、図5のように、凸多角形が原点(0, 0)を含むと仮定しましょう。
図5 原点を包含する凸多角形
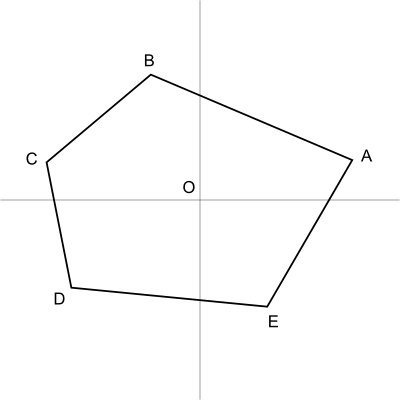
次に、図6のように、原点から凸多角形の各頂点へと線分を引きます。頂点をA, B, C, ...とすると、ベクトルA, B, C, ...は、まさにこれらの線分によって表されるベクトルとなります。
図6 各頂点のベクトル
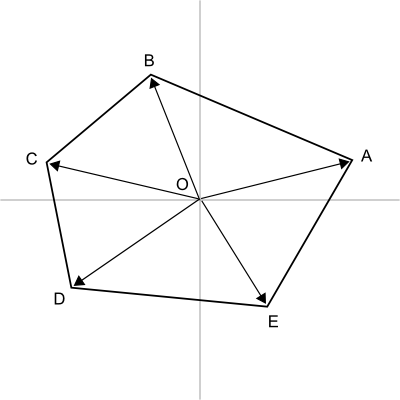
ここで、ベクトルAとベクトルBの外積がどんな量になるかを考えてみると、それは図7で示すような平行四辺形の面積です。ちょうど、三角形OABの面積の2倍になるわけです。
図7 ベクトルの外積
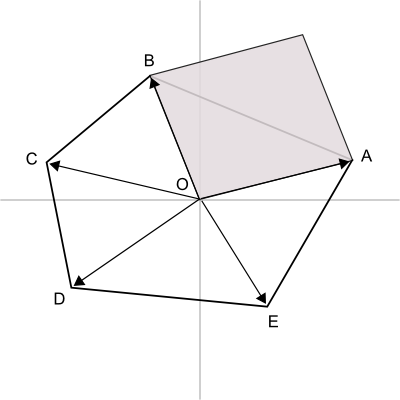
もうわかりましたね。AとBの外積、BとCの外積、...というように、隣り合う頂点のベクトル同士の外積をそれぞれ計算して合計し、2で割れば、凸多角形の面積が得られるのです。ただし、頂点の巡回順が時計回りの場合、この値は負になりますので、絶対値を見る必要があります。
そして、この外積を使った面積計算の方法は、多角形が原点を含まない場合でも、さらには多角形が凸でない場合(「五芒星」のように、辺同士が交差する場合は除く)でも、まったく同様に適用できてしまいます(なぜこのようなことが成立するのか、図を描いて考えてみてください)。
それでは、ConvexPolygonクラスに、多角形の面積を取得するgetArea()メソッドを追加してみましょう。
リスト getArea()メソッドの記述(Java)
public double getArea() {
double crossSum = 0; // 外積の合計
int size = vertices.size();
// 頂点を巡回
for (int i = 0; i < size; i++) {
Point2D v1 = vertices.get(i);
Point2D v2 = vertices.get((i + 1) % size);
// 外積を計算
double cross = GeomUtils.cross(v1, v2);
crossSum += cross; // 外積を加算
}
return Math.abs(crossSum / 2.0);
}
前々回の実装により、ConvexPolygonオブジェクトは、多角形の頂点を、反時計回りまたは時計回りの順番にしたがって、verticesフィールドに保持する仕様になっています。この前提があるため、verticesの要素を先頭から辿っていくことで、外積の計算に必要な隣接する頂点の組を順に得られることになります。
まとめと次回予告
今回は、多角形に対する演算として、点の包含判定と面積計算の2つを取り上げました。今回紹介した方法は、凸多角形クラスであるConvexPolygonのメソッドとして実装しましたが、凸でない多角形にも適用することができます。
今回作成したプログラムのソースコードがダウンロードできます。
次回は、凸多角形の「オーバーレイ」について考えます。お楽しみに!