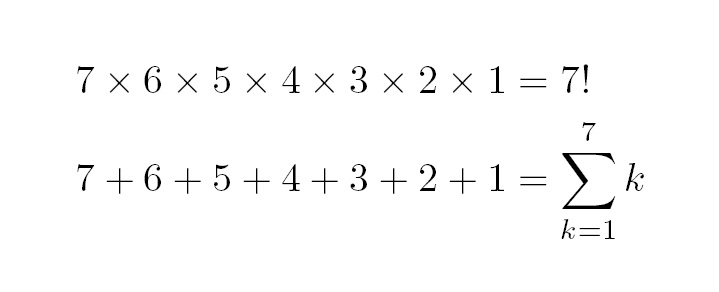記号化の基礎

数学が難しく感じるのは、さまざまな記号や長い数式に面食らうからではありませんでしたか？

しかし、ごひいきの野球チームのマーク・赤い提灯…。見慣れて親しんでしまった記号ならば条件反射、体が自然に反応してくれますよね。数学も同じです。初歩的な数学で済む間は、数学的な記号に慣れていれば、問題を型にはめてするりと解決してしまうこともあるのです。苦手意識を解消し、道具として積極的に数学の記号をプログラミングに役立てましょう。

記号化とは

記号化とは、数学的な概念や操作を簡略な記号で表すことです。例えば、仲間内ならば説明するより愛称（ニックネーム）で呼べば一言で誰だかわかります。同じように数学的な概念や操作に愛称をつけることが記号化なのです。記号を適切に用いることで、条件や状態を表す式を簡潔に、一見して読み取りやすく表現することができます。図2.1は、長々とした数式が記号によって劇的に見やすくなる例です。記号を多く知り、慣れておけば、数学的な問題への理解が早まり、問題解決の大きな助けとなるのです。

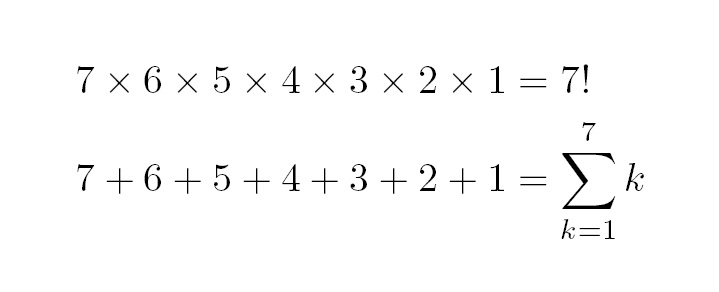
数学的な記号を知り、それを上手に使える人のことを、便利で磨き込まれた道具を持った名人大工に例えることができます（図2.2⁠）⁠。名人大工は適切に素材と道具を用い、無駄なく美しい仕事をしますね。プログラマも同様で、プログラミング言語は素材、数学的な知識は大工道具に例えられます。いつの日か、名人と呼ばれるようなプログラマになりたいですね。

数学の記号

記号化された数学的な概念の代表は0、1、2、…といった数字です。数字を組み合わせて数値を表現します。数学的な操作の代表は＋、－、×、÷という四則演算です。概念も操作も、必要に応じて先人により絶妙な記号化が施されているので、適切に利用すれば強力な助っ人になります。

そのほか高校までの数学で学習する、極限、集合、順列組合せ、微積…なども絶妙に記号化されています。これら全てに習熟しておくことに超したことはありませんが、計算が苦手でもコンピュータにその記号を使った演算をさせられるくらいには知っておいたほうが良いでしょう。

プログラミング言語と記号

さて、プログラミング言語で使用する数値や演算の記号は、純粋な数学の数値や記号と異なる意味を持つ場合があり、注意が必要です。

1. 整数と実数とでは、コンピュータ内部での表現方法が異なります。
2. プログラミング言語の実数型は、無理数や分数を表現できません。
3. ＋（プラス）演算子は文字列の連結や、論理和[1]の記号として用いるプログラミング言語があります。

上記はほんの一例です。プログラミング言語を利用するときには、思わぬ働きをして戸惑わないように、その言語に用意されている数値や演算記号の意味と働きをよく確認しておく必要があります。

数学では当たり前に使われる記号でも、プログラミング言語には用意されていないものがあります。プログラミング言語に用意されていない記号が必要になったら、プログラマがその働きをするプログラムを書くことになります。

数学からすこし外れますが、プログラマはプログラミング言語という記号の集まり用います。プログラムの設計をする場合は、フローチャートやUMLといった図面を用います。それらの図面も記号の集まりです。プログラマはまさに記号を扱う仕事なのです。

以上のように、より広い意味で記号化をとらえ、プログラミングに役立つ知識・技術を紹介します。

プログラミング言語で取り扱うことのできる数値

数学的には、全ての数は複素数にまとめられます。図2.3のように複素数は実数と虚数に分けられ、実数を更に細かく分類した末に整数があります。

Java言語では、図2.4のように、いくつかの数値型が用意されています。コンピュータはその仕組み上、この図のように分類する方が都合がよいのです。それぞれの数値型は取り扱える上限値や下限値があります。虚数や無理数の型はありません。実は少数のうちの多くは厳密に表現することができません。このあたりは、やがて浮動小数点数を学習するときに詳しく説明します。

Java言語では、文字型（char）を符号なしの整数型(16bit、0～65535)として用いることもできます。

問題：15!の計算をするプログラム

15!（15の階乗）の計算をする次のソースコードKaijyou15_1.javaの問題点を指摘し、修正しましょう。

（1）　ソースコードKaijyou15.javaを紙の上でトレースし、実行結果を予想してみましょう。

（2）　このコードを実行してみましょう。すると問題点が明らかになりますから、その原因を調査し解決策を提案してください。

（3）　正しい結果を出力するようにソースコードを修正してください。

1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:

//filename : Kaijyou15.java
class Kaijyou15 {
  public static void main(String[] args) { 
    double result1 = 0;  double result2 = 1;
    result1 = 15*14*13*12*11*10* 9
             * 8* 7* 6* 5* 4* 3* 2* 1;
    System.out.println("result1 = " + result1);
    for(int i = 15; i>=1 ; --i){result2 *= i; };
    System.out.println("result2 = " + result2);
  }// end of main
}// end of class

ヒント（1）

4行目には計算結果を格納する変数が宣言されています。これらの変数の型と格納可能な数値の範囲を確認しておきましょう。

ヒント（2）

5,6行目は1つめの計算式です。電卓で計算してみましょう。

ヒント（3）

Java言語は、5,6行目の計算式右辺の数値を、どの数値型と理解するでしょうか。コンピュータは式をひとかたまりとして処理せずに、基本的には左端から「ひとつひとつの数値」「⁠ひとつひとつの演算子」ごとに解釈してから処理します。

解説

（1）　ソースコードKaijyou15.javaを紙の上でトレースし、実行結果を予想してみましょう。

トレースした結果を図2.5に示します。別ウィンドウに前頁を開くか、プリントアウトして、ソースコードを参照しながらトレースを追ってみてください。なお、このトレースは、ソースコードの問題点に気づいていないという前提で作成しています。

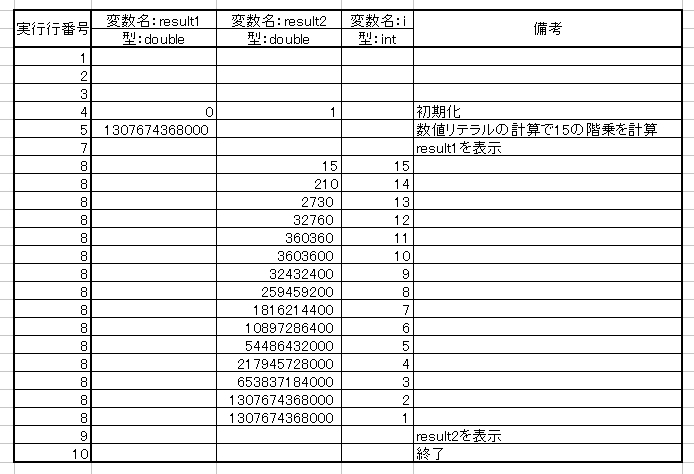
トレースの結果、どちらの場合も1307674368000と出力されるはずです。さてどうなるでしょうか？

（2）　このコードを実行してみましょう。すると問題点が明らかになりますから、その原因を調査し解決策を提案してください。

ソースコードを実行して、次のような出力を得ました。

result1 = 2.004310016E9
result2 = 1.307674368E12

2.004310016E9は、2.004310016×10⁹の意味です。

同じ計算をしたはずの２つの値が一致していません。どちらが正しい結果なのでしょう？　それとも、どちらも正しくないのでしょうか？

先にトレースしておいたので、「⁠どちらかといえば正しいと思われる結果」はresult2の1.307674368E12だとわかります。では、なぜresult1は正しい結果を得られなかったのでしょうか？

問題点は5、6行目の計算式にあります。右辺は一見、定義通りの全く問題ない式に思えます。しかし、Java言語の実行システムは、右辺に書かれた数値リテラル[2]をint型としてとらえ、左から順番に計算を実行します。このため、int型の処理可能な最大値2147483647を超過、すなわちオーバーフロー[3]すると、超過した桁は消えてしまいます。そしてその結果をもとに最後まで計算を続けてしまうのです。計算の結果が正しいかどうかはお構いなしです。

（3）　正しい結果を出力するようにソースコードを修正してください。

以上の調査・検討を元に、正しく動作するソースコードを作成します。

この課題だけに関していえば、解決は至極簡単です。行番号5、6の右辺で実行される計算が、int型と認識されたまま計算が進むことが問題なのですから、明示的にそれよりも大きな型の演算であることを指示すればよいのです。

（1）long型(長整数)にキャスト[4]する。

5:
6:

    result1 = (long)15*14*13*12*11*10* 9
             * 8* 7* 6* 5* 4* 3* 2* 1;

あるいは、次のように型を明示する方法もあります。

5:
6:

    result1 = 15L*14*13*12*11*10* 9
             * 8* 7* 6* 5* 4* 3* 2* 1;

こうすれば、最初の値15がlong型と認識され、以後の計算の結果はlong型で取り扱われます。long型の最大値9223372036854775807(19桁)までは安泰[5]です。Lは小文字でもかまいませんが、大文字のほうが読みやすく、小文字のlが数字の1と誤読されるのを防げます。

（2）double型(倍精度実数)にキャストする。

5:

    result1 = (double)15*14*13*12*11*10* 9

変数result1はdouble型なので、右辺をdouble型にキャストするのがより自然かもしれません。次のように型を明示する方法もあります。

5:

    result1 = 15d*14*13*12*11*10* 9

dは大文字でも良いのですが、大文字のDが数字の0と間違えやすいため、小文字をおすすめします。

次のようにすると、15がfloat型になります。

5:

    result1 = 15.*14*13*12*11*10* 9

残念ながらJava言語では、今回のような算術演算においてオーバーフローが発生しても例外やエラーが発生しません[6]⁠。オーバーフローの発生が予想される場合には、プログラマ側でそれに対応する処理を作ることが期待されているのです。

数値を計算するプログラムを作成する場合には、計算結果のみならず、計算途中の値が型に収まりきらない値にならないか注意を払う必要があります。

さて、次のコードKaijyou15_2.javaは正しい結果を得るためのコードの一例です。最初に示したプログラムを、ほんの一カ所変更しただけです。

1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:

//filename : Kaijyou15_2.java
class Kaijyou15_2 {
  public static void main(String[] args) { 
    double result1 = 0;  double result2 = 1;
    result1 = 15d*14*13*12*11*10* 9
              * 8* 7* 6* 5* 4* 3* 2* 1;
    System.out.println("result1 = " + result1);
    for(int i = 15; i>=1 ; --i){result2 *= i; };
    System.out.println("result2 = " + result2);
  }// end of main
}// end of class