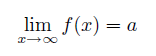前回は、数学とJava言語では数の分類名に同じ名前が用いられていても、取り扱える数値の範囲や意味に違いがあることを確認しました。プログラミング言語で使える数値型は案外窮屈なものなのです。
さて、今回と次回は演算記号を取り上げます。数学で用いる様々な演算記号が、Java言語のソースコードではどのように記述されるのかを確認します。紹介する演算記号がたくさんあるため、2回に分けて学びます。今回は記号たちを机の上にひろげて、1つひとつをながめてみましょう。そして次回、それぞれの記号を使ってみます。数が多いことに及び腰にならないで下さいね。どれも皆とてもシンプルなものばかりです。それでは、記号の工具箱を開くとしましょう[1] 。
図3.1 工具箱を開くプログラマ。工具箱は演算記号の宝箱各種の演算記号
四則演算
四則演算 は最も基本的な演算です。それぞれ、加算・減算・乗算・除算 といいます。表3.1 に四則演算記号の一覧表を示します。Java言語では乗算に * ( スター)を、除算に / ( スラッシュ)を用います。プログラミング言語では使える文字種に制限があるため、数学とは別の記号を割り当てられています。
表3.1 数学とJava言語の四則演算記号
数学 Java言語 加算 + + 減算 - - 乗算 × * 除算 ÷ /
剰余演算
剰余演算 とは、除算の余りを求める演算です。剰余演算は、数学では % や mod ( moduloの略)を用います。Java言語では、 % ( モジュロと読む)を用います。
c = a%b
と書くと、
a ÷ b = x … c
という除算の剰余が c に代入されるのです。
高校までの数学では剰余を求めるために特に記号を与えられませんでした。しかし、実生活の中には、剰余を求められると便利な場合が多くあります。ひとつ例を示しましょう。「 現在時刻は14時です。これから200時間後は何時でしょうか。」という問題。剰余記号を用いた演算ができればシンプルに記述できます。計算式は (200 + 14)%24 = 22 となり、答えは22時です。たった一行で表現できました。しかし、剰余記号を用いなければ、 (200+14)/24 = 8.916…、(200+14)-24×8 = 22 。細かいことを言えば、先の除算の結果を整数化する手続きが必要です。
等号
数学では、等号 = ( イコールと読む)は、等号を挟んだ式の左側(左辺)と右側(右辺)が「等しい」ことを意味しています。同様に、非等号 ≠(ノットイコールと読む)は左辺と右辺が「等しくない」ことを意味します。
プログラミング言語で等号は、左辺と右辺が「等しいかどうか」という用いられ方をするときと、右辺の計算結果を左辺に「代入 する」という用いられ方をするときがあります。この2つの用途を区別するためにJava 言語では、「 等しいかどうか」というときには == 、「 代入する」というときには = を用いて区別しています。「 等しくないかどうか」の場合は != と書きます。以上のことを表3.2 にまとめました。
表3.2 数学の等号とJava 言語の代入・比較演算子
数学 Java言語 代入 = 等しい = 等しいかどうか == 等しくない ≠ 等しくないかどうか !=
Java言語の算術演算子
Java言語は表3.3 のような算術演算子 を持っています。算術演算子には、これまでに紹介した四則演算子、剰余演算子の他に、代入演算子、単項演算子 があります。
表3.3 Java 言語の算術演算子
名称 演算子 四則演算子、剰余演算子 +、 -、 *、 /、 % 代入演算子 = 、+=、 -=、 *=、 /=、 %= 単項演算子 ++、 --
代入演算子とは、右辺の計算結果を、左辺に置かれた変数の値にするための記号です。プログラミングの初心者にとって、この代入の理解がどうも鬼門になるようです。数学では、イコールを挟んで右辺と左辺は等しいという意味です。左右の辺に現れる変数は“ 当然” 同じ値をとります。ところが、次の式を見てください。
i = i + 1;
プログラミング言語では、右辺の計算結果によって左辺の値が変わります。右辺の変数 i の値と、左辺の変数 i の値は異なるのです。この式を見て、「 プログラミング、やーめた」という人を何人も見てきました[2] 。もし、あなたがそうなら、「 イコールは、等号ではなくて、代入演算子です!」と3回唱えましょう。右辺の計算結果が左辺に代入されるのです。もし、この式の以前の変数 i の値が5ならば、この式の実行後、 i の値は6になります。そういうことなんだ、と信じてください。
i = i + 1 のように短い式なら良いのですが、ソースコード中の変数名というのは「値の意味を簡潔かつわかりやすく示すもの」になっています。短いほうがプログラマにとって入力が楽ですが、あまりに短いと意味不明になって逆に苦労をします。このため、プログラマは一般的に変数名をあまり短いものにしませんし、大文字・小文字・記号等を様々に織り交ぜます。数式もプログラムも長くなりがちです。
そのため、少しでも入力の手間を減らし、式を短くして一覧性をよくするために代入演算子 ( +=、-=、*=、/=、%= )が作られました。代入演算子を使うと、例えば someValue = someValue + 1は、someValue += 1 と簡潔に書けるのです。
さらに、この「1増やす(インクリメント) 」 「 1減らす(デクリメント) 」といった操作は、プログラムの中でたびたび出てきますので、単項演算子 ( ++ , -- ) が作られました。 ++i と書くと、変数 i の中身は1増えます。 --i と書くと、1減ります。 i++ や i-- も同様に理解して結構です。本当は、少し違いがあるのですが、その違いがプログラムに必要になったときには、多分ご自分ですぐに理解できる力を得ています。今はそういうものがある、というだけにしておきます。
不等号
不等号 は、左辺と右辺の大小関係を表す記号です。数学では、不等号を挟んだ左右の辺の大小関係は不等号が示すとおりでなくてはなりません。しかし、プログラミング言語では、不等号を挟んだ左右の辺の大小関係は不等号の示すとおりとは限りません。等号と同様、プログラミング言語における不等号は「大なりかどうか」「 小なりかどうか」を確かめる演算子なのです。Java言語では不等号と比較の等号・非等号( == と != )をあわせて比較演算子 といいます。演算の結果は真(True)か偽(False)という論理値です。
≥、≤の下側の一本線はイコール( = )を表しています。これを二本線で書く流儀もあります。
表3.4 に数学の不等号とJava 言語の比較演算子の一覧を示します。
表3.4 数学の不等号とJava 言語の比較演算子
数学 Java言語 大なり > 大なりかどうか > 小なり < 小なりかどうか < 大なりイコール ≥ 大なりイコールかどうか >= 小なりイコール. ≤ 小なりイコールかどうか <=
分数
分数 とは、括線 (「 かつせん」という。横棒のこと)の上下に数値を書いて表現されるもので、四則演算に置き換えると割り算と等価です。
括線の上の数を分子 、括線の下の数値を分母 といいます。分数を表す型はJava言語にはありませんので、分数の計算結果を実数型の変数に格納するか、分子・分母を別々の変数に格納するなどの工夫を必要とします。例えば、分子に対して分母が大変大きな数である場合、割り算してしまうとゼロとしか表現できなくなります。このような情報の消失を防ぐためには分子・分母を別々に保管することが有効です。
Mathクラス
ここでJava言語に用意されている便利なMathクラス を紹介します。今後紹介する数学記号は、このMathクラスで用意されています。
Mathクラスは、Java言語に用意されている数学処理用クラスです。特に宣言しなくても、ソースコード中で用いることができます。
b = Math.abs(-2);
上の例では、変数bに-2の絶対値2が代入されます。
そのほか累乗・平方根・対数・数字丸め・三角関数・角度換算といった処理を行うことができます。
このMathクラスはJavaのバージョンアップごとに関数が追加されています。JDK6でもかなりの数のメソッドが追加されています。ここでお話しした内容は次のWebサイトを元にしています。このサイトをブックマークに登録しておき、事あるごとに目を通す癖をつけるとよいでしょう[3] 。
Java™ Platform, Standard Edition 6 API Specification
http://java.sun.com/javase/6/docs/api/
[3] 入門者・初心者の方がJava 言語の文法や演算子に関する情報を得るには、技術評論社刊の『いちばんやさしいJava 入門 』( 丸の内とら著) が良いでしょう。先ずはこの小さな書籍を手元に置き、内容を一通り押さえましょう。
指数
指数 は、an のように書きます。これは数値aをn回掛け合わせるという意味です。nは任意の実数です(整数でなくてもよい) 。aを底 (てい。流儀によっては基数 と呼ぶ) 、nを指数といいます。指数のことを冪乗 (べきじょう) 、冪指数 (べきしすう)と呼んだりする流儀もあります。指数が0のときは、結果が1と定義されています。
Java言語では指数を演算子ではなくMathクラスのメソッドとして用意しています。an は次のように書くことができます。
c = Math.pow(a,n);
累乗根
累乗根 は、一般的には「n回掛け合わせるとaになる数値」を表しています。2回掛け合わせてaになる数値を平方根 () 、3回掛け合わせてaになる数値を立方根 (根 (こん)ということもあります。
累乗根は次のように指数形式に書き直すこともできます。
累乗根を冪乗根(べきじょうこん)と呼ぶ流儀もあります。Mathクラスには、平方根・立方根が用意されています。
c = Math.sqrt(a); //平方根
c = Math.cbrt(b); //立方根
その他の累乗根は指数を用いて書くことができます。5乗根の例を示します。
c = Math.pow(a,(1.0/5)); //5乗根
対数
対数 は指数の逆関数で、記号に log を用います。 c = loga b は、aを何回掛け合わせたらbになるのかをcの値とする、という意味です。aを底 、bを真数 といいます。ただし、対数は底に1をとることができません。
Java 言語には対数を計算するために自然対数(底はe)と常用対数(底は10)が用意されています[3] 。
プログラマは2を底とする対数が使えると便利です。ある数値が2進数で何桁になるか一度の計算でつかめます。例えば、log2 255 = 7.994…ですから、8ビットあれば足りることがわかります。
さて、2を底とする対数が必要になった場合は対数法則 (底の変換公式 )を使って対処しましょう。次の例では、2を底とする対数をbを底とする対数に変換しています。忘れてはならないのが、対数の底は1以外の正の実数であることです。
Java 言語では、対数は次のように使います。
b = Math.log(a); //自然対数
b = Math.log10(a); //常用対数
絶対値
絶対値 は、数値から正負の情報を取り去り、原点からその数値までの数直線上の距離を与えます。例えばb = |a|としたとき、bは数値aの原点からの距離を表します。
Java言語で絶対値を取得する場合は、コードを書いてもよいのですが、やはりMathクラスでシンプルに書く方を強くおすすめします。プログラマの間では「コードを書かなければバグは発生しない」という格言もあるぐらいですから。
Java言語では、次のように書くことができます。
b = Math.abs(a);
数列の和
数列の和 は、記号Σ(シグマ)を用いて書きます。 1 から n までの数の和は次のように書きます。
これは、変数 k を 1 から n まで1ずつ増加させ、そのひとつひとつの数を足しあわせることを意味しています。
残念ながら、数列の和をとるにはコードを組む必要があります。例えば1から5までの数の総和
他にも書き方があると思います。それぞれで工夫してみるとよいでしょう。
int sum = 0;
for(int k = 1; k <= 5 ; ++k){
sum += k;
}
極限値
極限値 は、記号 lim(リミット)を使って次のように書き表します。
この式で、ある関数 f(x) は、 x の値を無限大 にまで増加させたとき、ある値 a に限りなく近づくことを意味しています。勘違いしやすいことですが、関数の値が a になる、という意味ではありません。関数 f(x) の中身によっては、一定の値に近づくどころか変化し続けるものもありますし、無限大にまで大きくなっていくものもあります。変化し続けるものの好例はsin関数です。単純な一次関数 y = ax は無限大にまで大きくなります。
記号∞は無限大を表します。「 どんな数よりも大きい」という意味の記号で、数ではありません。Java言語の実数型にもInfinityという値がありますが、これは数学的な無限大を表すものではありません。実数型では表せない大きな数、という意味です。
無限小 という言葉もあります。これは「どんな数よりも小さい」という意味で微分ではdxと書きます。
Java言語の各数値型で取り扱える最大値や最小値を上手に活用すれば、極限値を近似、あるいは推測することが可能ですが、ここでは説明を割愛します。
階乗
階乗 とは1からnまでの自然数を全て掛け合わせたものです。記号 ! を用いて n! と書き、「 nの階乗」と読みます。
Java言語には階乗のための演算子やMathクラスのメソッドはありません。必要に応じて自分でコードを書く必要があります。
前回、階乗を通じてJava言語の数値型の窮屈さを実感してもらいました。階乗の値は、nの値に対して大変大きくなるため、必要な階乗のn値があらかじめ明らかならば、定数にしてコードに書いておく方が便利かもしれません。
static final long FACTORIAL_5 = 120;
階乗のための関数なんてわざわざ書いても、整数型で利用できるのはせいぜい20弱の階乗でしかありませんから。だからJava言語にも用意されていないのでしょうね。
三角関数
三角関数 とは、直角三角形の二つの辺と一つの角の間に成り立つ関数です。
Java言語では、Mathクラスに一通りの三角関数が用意されています。表3.5 に一部を紹介します。Mathクラスの三角関数では、引数の角度の単位に度([°])ではなくラジアン([rad])を用いるため、度を用いたい場合は換算関数を使用しましょう。
表3.5 Math クラスの三角関数関係メソッド
数学 Java言語 正弦 sinθ Math.sin(valR) 余弦 cosθ Math.cos(valR) 正接 tanθ Math.tan(valR) 逆正弦 arcsin xまたはsin−1 x Math.asin(ratio) 逆余弦 arccos xまたはcos−1 x Math.acos(ratio) 逆正接 arctan xまたはtan−1 x Math.atan(ratio) 度→ ラジアン Math.toRadians(valD) ラジアン→ 度 Math.toDegrees(valR)
ラジアンを用いた計算では円周率 (π)をよく用います。Java言語では、Mathクラスに Math.PI としてその値が格納されています。同様にMathクラスに格納されている定数にはネイピア数 (自然対数の底eのこと) Math.E があります。プログラム中で自分で定義してもよいのですが、せっかくきちんとした値が用意されていますのでこれらを活用するようにしましょう。
お疲れ様でした
記号の数々、いかがでしたか? 初めて出会う記号もあったことでしょう。このたび皆さんは、数学の記号と、Java言語の同じ記号の意味や使い方が違う場合があることを知りました。
次回は記号を実際に使ってみます。「 習うより慣れろ」という言葉がありますが、習ったら慣れましょう。幸い記号は使ってもすり減りません。むしろ使うほどに切れ味が良くなる道具です。問題という材料も無数にころがっています。次回までに、そこら中の材料をくっつけては切り刻んでみてはいかがでしょうか。

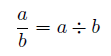
![]() と書き表されます。これは
と書き表されます。これは![]() )、
)、![]() ) といいます。nには任意の実数を使うことができます。累乗根の値を単に根
) といいます。nには任意の実数を使うことができます。累乗根の値を単に根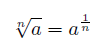
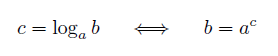
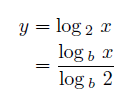
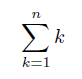
![]() は次のようなコードにできるでしょう。
は次のようなコードにできるでしょう。