前回は基本的な演算記号を採り上げました。今回は問題を通して具体的に取り組んでいきます。実際にソースコードを組んで実行してみましょう。眺めたり読んだりするだけでは決して得られないものがあるはずです。
問題:数学記号・Java言語の演算子を使ってみよう
(1) その結果を表示するためのソースコードを、リスト4.1のEnzanshi_Test.javaに付け加えてください。円周率、ネイピア数といった定数値はMathクラスに定義されているものを取り出してください。また、変数a、b、cはソースコード内に定義したものを利用してください。その他、必要な変数があれば適宜宣言して利用してください。
(2)
(3) 予想した結果と比較してみましょう。
① 四則演算、剰余演算
a + b - c
a × b ÷ c
a % b
② 等号・不等号
a の値を c に代入
c の値と a の値が等しいかどうか
c の値と a の値が等しくないかどうか
a の値より b の値が大きいかどうか
a の値より b の値が小さいか等しいかどうか
③ 代入演算子
c に 2 を代入
+= を使って c + a の結果を c に代入
-= を使って c - a の結果を c に代入
*= を使って c × a の結果を c に代入
/= を使って c ÷ a の結果を c に代入
%= を使って c mod a の結果を c に代入
④ 単項演算子
c の値を表示
++c を実行
c の値を表示
c++ を実行
c の値を表示
--c を実行
c の値を表示
c-- を実行
c の値を表示
⑤ 累乗・累乗根・対数・絶対値・無限大
loge a
log10 a
log2 a
-5の絶対値
単精度実数型の最大値
単精度実数型の最大値×2
(※単精度実数型の最大値はFloat.MAXVALUE で取得できます。)
⑥ 数列の和・階乗
5!
⑦ 三角関数
円周率(π)の値
30°をラジアンに換算
60°をラジアンに換算
sin 30°の値
sin
ネイピア数(e)の値
リスト4.1 Enzanshi_Test.java
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
//filename : Enzanshi_Test.java
class Enzanshi_Test {
public static void main(String[] args) {
float a=10; float b=5; float c=2;
System.out.println("(a,b,c)=( "+a+" , "+b+" , "+c+" ) とする。");
//ここにプログラムを書き足しましょう。
}// end of main
}// end of class
解説
(1) その結果を表示するためのソースコードを、リスト4.1のEnzanshi_Test.javaに付け加えてください。円周率、ネイピア数といった定数値はMathクラスに定義されているものを取り出してください。また、変数a、b、cはソースコード内に定義したものを利用してください。その他、必要な変数があれば適宜宣言して利用してください。 リスト4.2に解答例を示します。大変長いソースコードになりましたが、上から下へ流れるシンプルなものですから大丈夫でしょう。おそらく、作成に困ったのではないかと推測されるのが36行目の2を底とする対数です。底の変換公式を上手に活用してください。逆正弦関数(Mathクラスを上手に組み合わせることが大変だったのではないでしょうか。
ソースコード中のSystem.out.printlnメソッドの引数の中での + の使い方に注目してください。このメソッドの引数は最終的に一連の文字列に変換されます。引数が "a = " + a のときは、文字列と数値を連結するために + が用いられています。ところが、 "a + b = " + ( a + b ) として加算も実行できています。仮に"a + b = " + a + b として実行するとどうなるでしょうか。確かめてください。
その他のところも、いろいろと変更して遊んでみてください。
リスト4.2
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19:
20:
21:
22:
23:
24:
25:
26:
27:
28:
29:
30:
31:
32:
33:
34:
35:
36:
37:
38:
39:
40:
41:
42:
43:
44:
45:
46:
47:
48:
49:
50:
51:
52:
53:
54:
55:
56:
57:
//filename : Enzanshi_Test.java
class Enzanshi_Test {
public static void main(String[] args) {
float a=10; float b=5; float c=2;
System.out.println("(a,b,c)=( "+a+" , "+b+" , "+c+" ) とする。");
System.out.println("★四則演算、剰余演算★");
System.out.println("a+b-c="+(a+b-c));
System.out.println("a*b/c="+(a*b/c));
System.out.println("a%b="+(a%b));
System.out.println("★等号・不等号★"); c = a;
System.out.println("代入:c=a , c="+c);
System.out.println("比較:c==a は"+(c==a));
System.out.println("比較:c!=a は"+(c!=a));
System.out.println("比較:a<b は"+(a<b));
System.out.println("比較:a>=b は"+(a>=b));
System.out.println("★代入演算子★"); c = 2;
System.out.println("(a,b,c)=( "+a+" , "+b+" , "+c+" ) とする。");
c+=a; System.out.println("加算代入: c+=a c="+(c));
c-=b; System.out.println("減算代入: c-=b c="+(c));
c*=b; System.out.println("乗算代入: c*=b c="+(c));
c/=b; System.out.println("除算代入: c/=b c="+(c));
c%=b; System.out.println("剰余代入: c%=b c="+(c));
System.out.println("★単項演算子★");
System.out.println("単項加算前置:"+"c="+(c)+" ++c="+(++c));
System.out.println("単項加算後置:"+"c="+(c)+" c++="+(c++));
System.out.println("単項減算前置:"+"c="+(c)+" --c="+(--c));
System.out.println("単項減算後置:"+"c="+(c)+" c--="+(c--));
System.out.println(" c="+(c));
System.out.println("★累乗、累乗根★");
System.out.println("a のb 乗="+(Math.pow(a,b)));
System.out.println("a の平方根="+(Math.sqrt(a)));
System.out.println("a の5 乗根="+(Math.pow(a,1.0/5.0)));
System.out.println("★対数、絶対値、無限大★");
System.out.println("自然対数(底はe) log_e(a) ="+(Math.log(a)));
System.out.println("常用対数(底は10)log_10(a)="+(Math.log10(a)));
System.out.println("2 を底とする対数log_2(a) ="+(Math.log(a)/Math.log(2)));
System.out.println("-5 の絶対値|-5|="+(Math.abs(-5)));
System.out.println("単精度実数の最大値="+(Float.MAX_VALUE));
System.out.println("単精度実数の最大値*2="+(Float.MAX_VALUE * 2));
System.out.println("★数列の和、階乗★");
int sum=0; for(int k=1; k<=5; ++k){sum+=k;}
System.out.println("1 から5 までの数列の和="+sum);
int fact=1; for(int k=1; k<=5; ++k){fact*=k;}
System.out.println("5!="+fact);
System.out.println("★三角関数★");
System.out.println("円周率の値は? ="+Math.PI);
System.out.println("30 度は何ラジアン?="+Math.toRadians(30));
System.out.println("60 度は何ラジアン?="+Math.toRadians(60));
System.out.println("π/6 は何度? ="+Math.toDegrees(Math.PI/6));
System.out.println("π/3 は何度? ="+Math.toDegrees(Math.PI/3));
System.out.println("sin 30° ="+Math.sin(Math.toRadians(30)));
System.out.println("sin π/6 ="+Math.sin(Math.PI/6));
System.out.println("arcsin(1/2) ="+Math.asin(1.0/2)+"[rad]");
System.out.println("度になおすと・・・="+Math.toDegrees(Math.asin(1.0/2)));
System.out.println("おまけにネイピア数="+Math.E);
}// end of main
}// end of class
(2) 一通り関数電卓を使って確かめてみてください。関数電卓で確かめることにより、入力の順番を誤っていないかをチェックできます。電卓同様、間違った手順ではコンピュータも正しい計算をしてくれません。
(3) 予想した結果と比較してみましょう。 三角関数の計算結果には特に注目してください。30度、60度といったわかりやすい角度を用いたにもかかわらず、計算結果には少し誤差が生じているのがわかります。プログラミング言語を使った計算は、こういうものなのだ、と知っておいてください。
53行目の逆正弦関数計算を、次のように“ 素直に” 記述した場合はどんな結果が出るでしょうか。どうしてこれではおかしな結果になるのか、自分で実験して考えてみてください。
53:
System.out.println("arcsin(1/2) = "+Math.asin(1/2)+"[rad]");
それでは実行結果を図4.1に示します。ご自分の実行結果と一致しているでしょうか。一致していなければ、なぜ一致しないかの理由を突き止めましょう。なんとなく修正したら同じ結果が得られた、というだけでは今回のポイントを見落としてしまうかもしれませんよ。
図4.1 Enzanshi_Test.javaの実行結果
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19:
20:
21:
22:
23:
24:
25:
26:
27:
28:
29:
30:
31:
32:
33:
34:
35:
36:
37:
38:
39:
40:
41:
42:
43:
44:
45:
46:
47:
48:
49:
(a,b,c)=( 10.0 , 5.0 , 2.0 ) とする。
★四則演算、剰余演算★
a+b-c=13.0
a*b/c=25.0
a%b=0.0
★等号・不等号★
代入:c=a , c=10.0
比較:c==a はtrue
比較:c!=a はfalse
比較:a<b はfalse
比較:a>=b はtrue
★代入演算子★
(a,b,c)=( 10.0 , 5.0 , 2.0 ) とする。
加算代入: c+=a c=12.0
減算代入: c-=b c=7.0
乗算代入: c*=b c=35.0
除算代入: c/=b c=7.0
剰余代入: c%=b c=2.0
★単項演算子★
単項加算前置:c=2.0 ++c=3.0
単項加算後置:c=3.0 c++=3.0
単項減算前置:c=4.0 --c=3.0
単項減算後置:c=3.0 c--=3.0
c=2.0
★累乗、累乗根★
a のb 乗=100000.0
a の平方根=3.1622776601683795
a の5 乗根=1.5848931924611136
★対数、絶対値、無限大★
自然対数(底はe) log_e(a) =2.302585092994046
常用対数(底は10)log_10(a)=1.0
2 を底とする対数log_2(a) =3.3219280948873626
-5 の絶対値|-5|=5
単精度実数の最大値=3.4028235E38
単精度実数の最大値*2=Infinity
★数列の和、階乗★
1 から5 までの数列の和=15
5!=120
★三角関数★
円周率の値は? =3.141592653589793
30 度は何ラジアン?=0.5235987755982988
60 度は何ラジアン?=1.0471975511965976
π/6 は何度? =29.999999999999996
π/3 は何度? =59.99999999999999
sin 30° =0.49999999999999994
sin π/6 =0.49999999999999994
arcsin(1/2) =0.5235987755982989[rad]
度になおすと・・・=30.000000000000004
おまけにネイピア数=2.718281828459045
前回と今回にわたり、Java言語の数値演算に関する記号の工具箱をひっくり返してみました。いかがでしたか? プログラミング言語は、入門書の説明を一通り読むだけで終わらせないで、今回のようにひっくり返してはいじってみてください。そうすることで、「 あ、こんなことができた!」「 これはこんな風になった!」ということがつながり、いつの間にか役に立つ知識・技術になるのです。
こうして得た経験は、そう忘れてしまうものではありません。記号は道具です。道具は使ってこそ役に立ちます。電卓代わりにプログラムを作って計算しましょう。ぜひとも楽しんで、いじり倒してみてください。
今回のまとめ
Java 言語で計算を行うには、用意された演算子を使う方法、Mathクラスに用意されたメソッドを使う方法、自分で演算を組み立てる方法があります。
数学とJava言語では同じ記号でも意味や使い方が異なるものがあります。
ソースコード中の数値リテラルの型には注意しましょう。
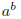
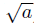
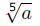
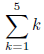
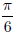 を度に換算
を度に換算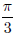 を度に換算
を度に換算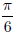 の値
の値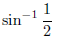 の値
の値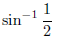 の演算結果を度単位に換算
の演算結果を度単位に換算![]() ) のところも、
) のところも、


