[1]。
図6.1 見た目はいっしょ。中身は?

記数法と基数
2進数・10進数・16進数などといった数値の表現方法を記数法といいます。記数法とは、適当な文字と記号を用い、特定の規則で数値を表現することです。2・10・16といった数を、それぞれの記数法の基数(きすう)といいます。基数とは、桁上がりするときの数の大きさのことです。
これら基数の異なる記数法間の換算を簡単にできる電卓もありますが、桁数が小さな数値であればちょいっと筆算や暗算できるといいですね。
2進数・10進数・16進数の相互変換
2進・10進変換
2進数とは、数を0と1だけで表現する方法です。例えば10進数の0、1、2は、2進数では(0)B,(1)Bと数え、次で桁上がりし、(10)B となります。2進数の数値に( )Bを付けて記述するのは、他の記数法と明確に区別するための工夫です。同様の意味で10進数の数値には( )D、16進数の数値には( )Hを用います。
正の整数の変換方法
2進数と10進数の間の正の整数の変換方法を次に示します。2進数から10進数への変換については数学記号を用いて1つの式の形にきれいにまとまります。10進数を2進数に変換する方法は文章にしています。途中でいくつかの判断と、処理の分岐が必要なためです。まるでプログラムのようですね。
10進数から2進数への変換方法は、ちょっと言葉が難しかったでしょう。しかし、実際に手を動かしてみると難しくはないんです。図6.2にその手順を示します。この例にならって、(1101)Bを10進数に、(25)Dを2進数に変換してみてください[2]。
図6.2 2進←→10進変換

小数を含む数の変換方法
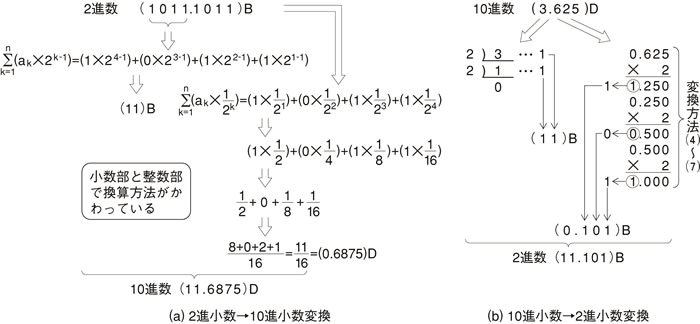
次に少数を含む場合の数の変換方法を示します。基本的に整数の変換方法と同じなのですが、少しだけ違いがあります。具体的な変換の様子を図6.3に示しました。整数部分には整数の変換方法を、小数部分には小数の変換方法を適用しているのを確認してください。この例にならって、(0.0111)Bを10進数に、(0.5625)Dを2進数に変換してみてください[3]。
10進数の小数部分を2倍した結果が0にならないと、永遠にこのアルゴリズムは終わりません。このため、コンピュータである小数を2進数に変換する場合は、表現可能な桁数を超えた時点で変換を打ち切ります。ここで生じる誤差、打ち切り誤差については、この連載中もうしばらくしてから浮動小数点数のところで詳しく述べることにします。
図6.3 2進小数←→10進小数変換
2進・16進変換
2進数と16進数は次の表のようにわかりやすく対応しています。トレーニングのつもりで、対応をあらわした表6.1を3回書き写してみましょう。すぐに覚えてしまいますよ。
表6.1 2・10・16進数対応表
| 10進数 | 16進数 | 2進数 |
|---|
| 0 | 0x0 | 0000 |
| 1 | 0x1 | 0001 |
| 2 | 0x2 | 0010 |
| 3 | 0x3 | 0011 |
| 4 | 0x4 | 0100 |
| 5 | 0x5 | 0101 |
| 6 | 0x6 | 0110 |
| 7 | 0x7 | 0111 |
| 8 | 0x8 | 1000 |
| 9 | 0x9 | 1001 |
| 10 | 0xa | 1010 |
| 11 | 0xb | 1011 |
| 12 | 0xc | 1100 |
| 13 | 0xd | 1101 |
| 14 | 0xe | 1110 |
| 15 | 0xf | 1111 |
対応表が頭に入っていれば、どんなに桁数が多くなっても2進数と16進数の間の変換は簡単です。
(0xac)H = (1010 1100)B , (0xb2e)H = (1011 0010 1110)B
2進数は4桁ごとにひと桁の16進数に対応させて読むのです。どうですか? 初めての方はあまりのシンプルさにびっくりしませんか?
10進・16進変換
16進数とは、基数が16の記数法のことです。(0x0)Hから(0x9)Hまで数えた後、(10)Dを(0xa)H、(11)Dを(0xb)Hと順次表現し、(15)Dにあたる(0xf)Hの次で桁上がりし、(0x10)H(「いちぜろ」、または「いちまる」と読む)と数える方法です。10進数と16進数の混乱を避けるため、16進数は頭に0xを付け、さらに( )Hで数を囲みます。この連載中では(0x2e)Hのような表記方法をとります。
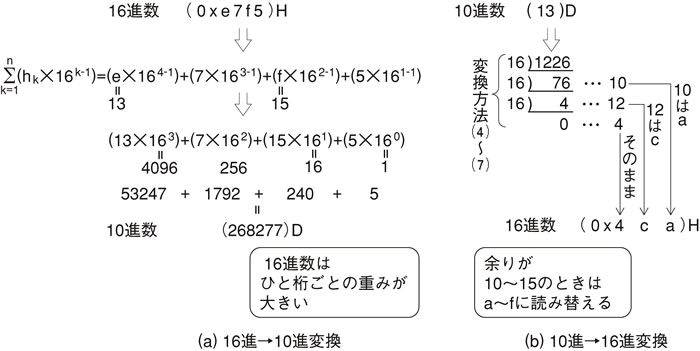
それでは、図6.4に筆算の様子を示します。この例にならって(0x100)Hを10進数に、(255)Dを16進数に変換してください[4]。
図6.4 10進←→16進変換の筆算
負数
負数とは、0より小さい数のことです。ここでは負の整数に限ってお話しします。
負の整数を表すために、コンピュータ内部では2の補数を用います。2の補数では、最上位のひと桁が符号ビットであり、正負の記号を表しています。このため、絶対値が2進数数値にしてn桁あるものを2の補数で表現するためには(n+1)ビット[5]が必要です。プログラミング言語で数値を取り扱う場合には、先ず数値の入れ物である数値型のビット数が決まっています。符号ビットである最上位桁をのぞいた部分が数値を表しているわけです。最上位ビットが0 であれば正の数を表しており、1であれば負の数です。
それでは、次の手順を使って、(-8)Dを2の補数の2進数に、2の補数の(1011)Bを10進数に変換してください[6]。
2の補数を10進数に変換する方法は、この方法を逆順に実行すればよいのです。
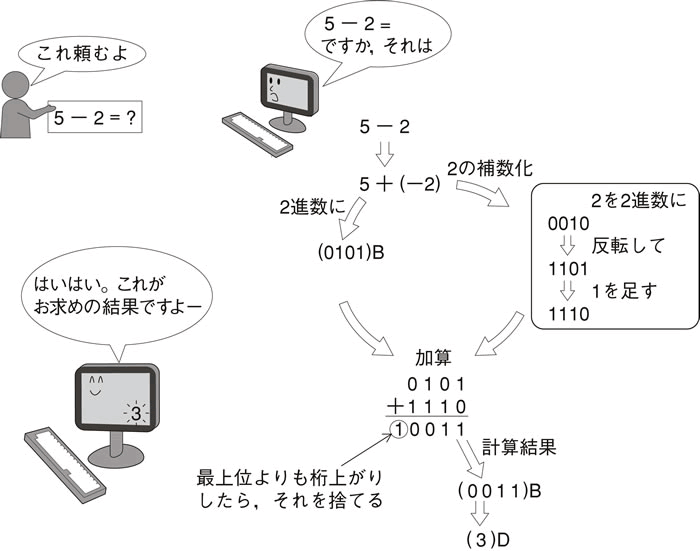
負数aを2の補数で表現しておけば、通常の2進数bと加算(b+a)の手続きを実行することで減算(b-a)ができるという利点があります。図6.5にその様子を示しました。図中で数値を4桁の2進数に変換しています。これは(5)Dが3桁の2進数になるため、符号を表すためにもうひと桁必要だからです。(2)Dは2桁の2進数ですが、(5)Dと符号付きの計算を行うために、桁数をあわせる必要があるので4桁の2進数に変換するのです。
図6.5 2の補数を用いた減算の様子
int型、long型に格納された数値に関する補足
これまで2・10・16進数それぞれの表現方法、相互の変換方法を学びました。これをJava言語をはじめとするプログラミング言語に活用するためにもう1つ知っておくべきことがあります。
それは、「プログラミング言語では数値を特定の型の変数に記憶させて用いる」ということです。このため、数値を記憶させた変数の型により、自動的に数値の「桁数」が固定されるのです。例えば10進数の1という数値はひと桁、2進数に変換してもひと桁なのですが、int型に代入された時点で32桁(32ビット) の数値になります。
このことを部屋の片付けに例えてみましょう。
「散らかった部屋を片付けるために、押し入れにぴったり収まる幅の、同じ大きさの箱をたくさん用意しました。一つの箱には一つのものしか入れない約束を作りました。ですから鉛筆1本でもひと箱使います。大きなぬいぐるみでもひと箱です。こうして全ての物を箱にしまい、押し入れにきれいに並べて片付けが終わりました。」
このたとえ話の中で、押し入れはメモリ、箱がint 型の変数を表しています。コンピュータはこのようにメモリと変数を取り扱います。変数に代入される値が大きかろうが小さかろうが同じだけのメモリの「幅」を必要とするので、空いたところには詰め物を必要とします。1本の鉛筆は10 進数の正の整数値1のことです。大変小さいのでわずかなスペースしか必要ないのですが、1つのものにひと箱と約束しましたので仕方ありません。そこで、空いたところには0という詰め物をします。大きなものでもその箱に入る限りは納めることができます。大きなぬいぐるみは大きな数値を表しています。空いたスペースはわずかですが、そこにも0が入ります。
より具体的に示しましょう。数値(1)D は(1)Bなのですが、int型の変数は32ビットほどの桁数を持っていますから、コンピュータは次のように記憶します。
(0000 0000 0000 0000 0000 0000 0000 0001)B
long型の変数を使った場合は64ビットですから、この倍の大きさの入れ物に数値を格納するのです。余った桁にはゼロが入ります。
それでは、(-1)Dはどうでしょうか。
先ほどこのように学習しました。
コンピュータで2の補数を取り扱う場合、次のように手順を修正します。
型変換は、数値が記憶される変数の型によって手順が変化するのです。このことを覚えておきましょう。見ていただいたとおり、2進数で数値を表現すると桁数が多くなりますので、16進数に読み替えます。2進数から16進数への読み替えは大変簡単でしたね。(1)D は(0x0000 0001)H、(-1)Dは(0xffff ffff)Hとなります。コンパクトでずいぶん読みやすいでしょう?
今回はここまで
次回は変数に格納された数値を16進数表示させてみます。これにより、今回学んだ知識、技術を具体的に確認していきます。








