コンピュータの処理能力は有限です。これを最大限に活用するために仕方なく生じる誤差があります。コンピュータを使う我々は、この誤差に上手に対処する必要があります。
それはちょうど、のこぎりの刃の厚みに例えることができます。のこぎりで木を切るためには、刃の厚みが薄ければ薄いほど便利です。しかし、あまりに刃が薄いと、引くときは良いのですが押すときに刃がしなってしまいます。のこぎりの刃の厚みは、使いやすさの視点から現在の厚みに落ち着いているわけです。
道具は使いやすさのために、なにがしかの妥協を必要とする点があるものです。上手にコンピュータで計算を行うために、今回の項目をしっかり理解しておきましょう。
図12.1 道具の弱点を逆に活かすのが「技」

浮動小数点数で発生するエラーや誤差
浮動小数点数の仕組み上避けられないエラーや誤差には次に挙げるものがあります。
- オーバーフロー/アンダーフロー
- 桁落ち
- 丸め誤差
- 情報欠落
- 打ち切り誤差
今回はこのうち「丸め誤差」と「情報欠落」を学習しましょう。
丸め誤差
丸め誤差とは、丸め操作(切り上げ・切り捨て等)を行った時に入り込む誤差のことです。
丸め誤差は、演算や代入により、数値をfloat型やdouble型に格納する際に生じます[1]。
コンピュータ内部で数値は2進数で表現されているため、有効桁数の大きい数値や、無限小数になる場合など、仮数部の桁数(ビット数) で表現できない下位の部分は、IEEE754で規定されたルールに従って丸めます。当然ながら誤差が出ます[2]。
IEEE754で規定された丸めのルールには、次の4つがあります。
- 最近値(最も近い値に丸める)Round to Nearest
- 上向き丸め(正の無限大側の値に丸める)Round to Plus ∞
- 下向き丸め(負の無限大側の値に丸める)Round to Minus ∞
- 切り捨て(絶対値が小さい側の値に丸める)Round to Zero
Java 言語ではこれらのうち最近値(RN)を標準の丸め方式としています。
たとえば、0.05 は2 進数にすると、次のような循環小数になります。
(0.00 0011 0011 0011 ...)B
float 型にこの値を格納する際には、次の二つのどちらかの値に決定しなければなりません。
V1 = (0 0111 1010 100 1100 1100 1100 1100 1100)B (0x3d4c cccc)H
V2 = (0 0111 1010 100 1100 1100 1100 1100 1101)B (0x3d4c cccd)H
真の値VPは(0x3d4c cccc ・ ・ ・)H です。VPがどちらの値に近いか減算をしてみましょう。

こうして真の値VPはV2により近いことがわかります。Java言語はこのようにして最も近い値を選択しているのです[3]。
float型は10進数にして8桁、double型で16桁程度しか有効数字がないため、高い精度を要求する計算では丸めによって生じる誤差が無視できない場合があります。例えば金銭の計算では、丸め誤差に当たる金額が、指数部の値によっては大金になります。過去には丸めで生じた金額を自分の口座に振り込み、ちりも積もれば山となる、で大金をせしめる犯罪がありました[4]。現在では金融システムでは金額の格納に実数型を用いないそうです。
情報欠落
情報欠落とは、2つの数の加減算を行うための桁あわせにより、一方の数値の仮数部が表現可能範囲から押し出されてしまうことです。
浮動小数点数では、指数部の値を同じにしてから加減算を実行します。指数部の大きい方にあわせて指数部の小さい方の数値の指数を変更すると、仮数部の値が右へシフトします。このシフト量が大きいと、仮数部の大部分が表現できる範囲を超えてシフトしてしまいます。このようにもともと格納されていた数値情報がシフトされることにより、一部または全部が消えてしまうことを情報欠落といいます。
コードを用いて具体的に説明します。
float a = 1e20;
float b = 1;
float c = a + b;
このコードはJava 言語により次のように解釈されます。
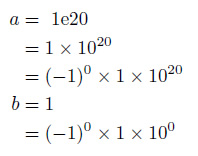
実数型の加減算は、指数部を大きい方にそろえたうえで、仮数部のみの加減算を行います。

上の式のように、bの指数部が20になります。すると、bの仮数部は0.00000000000000000001になります。float型の仮数部は10進数にして8桁程度しかありませんから、これだけの深い小数を格納することはできません。それで変数bの値は0になってしまいます[5]。
この結果、cの値は1e20となります。
たった一度の計算であれば、これほどの精度が必要な場合は希でしょう。しかし、このごくわずかな値の変化を数多く累計するような場合には注意が必要です。わずかずつでも引いたり足したりしていけば、いつかは値に大きな変化が現れるはずなのですが、浮動小数点数のこの仕組みのため、そうならないのです。
問題:下記の計算式を実行するソースコードを作成し、結果を表示しなさい。

(1)式に忠実にソースコードを作成し、実行しましょう。
(2)2つの式は数学的には全く等価なのに、どうして異なる演算結果になるのか、説明しましょう。
解説
(1)式に忠実にソースコードを作成し、実行しましょう。
以下にソースコードを示します。
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
|
//filename : Ketsuraku.java
class Ketsuraku {
public static void main(String[] args) {
float f1=1e+20f;
float f2=1e+20f;
float f3=1;
float result = 0;
System.out.println("f1 = " + f1);
System.out.println("f2 = " + f2);
System.out.println("f3 = " + f3);
result = (f1-f2)+f3;
System.out.println("(f1-f2)+f3 = " +result);
result = f1-(f2-f3);
System.out.println("f1-(f2-f3) = " +result);
}
}
|
|---|
実行結果を次に示します。
Ketsuraku.java の実行結果
f1 = 1.0E20
f2 = 1.0E20
f3 = 1.0
(f1-f2)+f3 = 1.0
f1-(f2-f3) = 0.0
(2)2つの式は数学的には全く等価なのに、どうして異なる演算結果になるのか、説明しましょう。
前者の式では絶対値の等しい数値を減算することでゼロとなります。これに1を加えているので結果は1です。
しかし後者の式はそうなりませんでした。浮動小数点数は加算を行う場合、ふたつの数値の指数部を指数の大きい方にそろえます。f3は、f2に指数部をそろえると、仮数部の値は小数点以下に19もゼロが続いた先にやっと1が現れます。float型の仮数部は10進数にして8桁程度しかありません。このため、1という数値は1×1020との演算の際に仮数部に表現可能な桁数から欠落し、0としか表現できなくなってしまうのです。
プログラム中の計算式は基本的に左から右へ計算されます。数学的には同じ式でも、加減算の順に注意しないと、今回の問題のように望まない結果となってしまいますので注意が必要です。