前回は、命題から真理値表をつくり、真理値表から論理式をたてる方法を詳しく学びました。今回はその確認として、いくつかの命題から論理式をたててみましょう。
問題:以下に示す命題を、真理値表を使って論理式の形にしましょう。
(1)「条件A、B、C のうち、一つだけ真のとき論理値Z は真である。」
(2)「条件A、B、C のうち、ふたつだけ真のとき論理値Z は真である。」
(3)「条件A、B のうち、ひとつだけ真のとき論理値Z は真である。」
(3) はエクスクルーシブ・オアの定義です。連載第15回で論理演算子を紹介した際、エクスクルーシブ・オアが3 つの論理演算を組み合わせたものである、と紹介しましたね。今回それが明らかになりますよ。
解説
問題:以下に示す命題を、真理値表を使って論理式の形にしましょう。
(1)「条件A、B、C のうち、一つだけ真のとき論理値Z は真である。」
先ずは、真理値表を作ります。
表18.1 問題(1) の真理値表
| A | B | C | Z |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
この真理値表から、Z が真の場合は三つだとわかります。この三つの場合の論理和が求める論理式です。
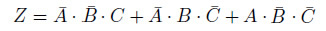
(2)「条件A、B、C のうち、ふたつだけ真のとき論理値Z は真である。」
先ず真理値表を作ります。
表18.2 問題(2) の真理値表
| A | B | C | Z |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
この真理値表から、Z が真の場合は三つだとわかります。この三つの場合の論理和が求める論理式です。
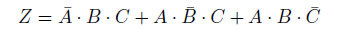
(3)「条件A、B のうち、ひとつだけ真のとき論理値Z は真である。」
先ず真理値表を作ります。
表18.3 問題(3) の真理値表
この真理値表から、Z が真の場合はふたつだとわかります。このふたつの場合の論理和が求める論理式です。エクスクルーシブ・オアは、このような演算を1つの記号⊕で表しているのです。
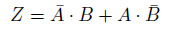
次のステップ、論理代数の各種演算公式を使いこなせば、真理値表からたてた論理式を、ひらめきに頼らずシンプルに変換することが可能になります。お楽しみに。
![]()
![]()
![]()



