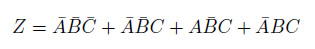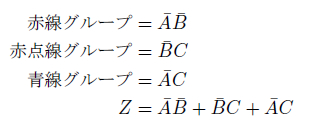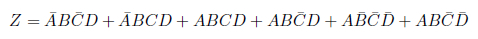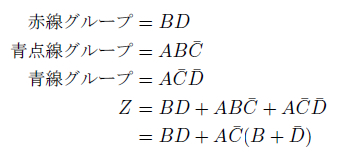カルノー図を大工仕事にたとえると、「⁠仕事を簡単に手早く済ませるための虎の巻」に納められた貴重なノウハウのひとつです。虎の巻にのっている仕事の手順やコツを利用すれば大変な時間の節約になります。

今回ご紹介する3変数や4変数の論理式を整理したい場合、論理代数の公式を活用しても同じ結果が得られます。しかし、カルノー図を利用すると莫大な筆算の手間を省くことができるのです。これを利用しない手はありません。どうぞ、この素敵な道具、カルノー図をご活用ください。

前回までの復習

これまでに2変数の場合のカルノー図の作り方・使い方を学びました。今回は3変数・4変数の場合のカルノー図を学びます。変数の数が増えますが、表の形が少々異なるだけで、基本的な手順は全く同じです。前回までに学んだ手順を確認しましょう。

1. カルノー図の枠を書く。
2. 与えられた論理式のそれぞれの項に対応するマスにチェックを入れる。
3. チェックをグループ化（隣り合ったチェックを四角形で囲む⁠）⁠。
4. グループ化したものを論理式にする。ひとつの囲みがひとつの項になる。
5. 全ての囲みから作った項の論理和をとる。以上、終わり。
6. ただし、囲みの形はなるべく大きな長方形か正方形であること。L字形や凹凸形にならないこと。

思い出せましたか？では、具体的な例を用いて、論理変数が3つの場合・4つの場合のカルノー図の作成と式の整理の様子を見ていきましょう。

3変数・4変数のカルノー図の作り方

図26.2に3変数・4変数のカルノー図の作り方を示します。

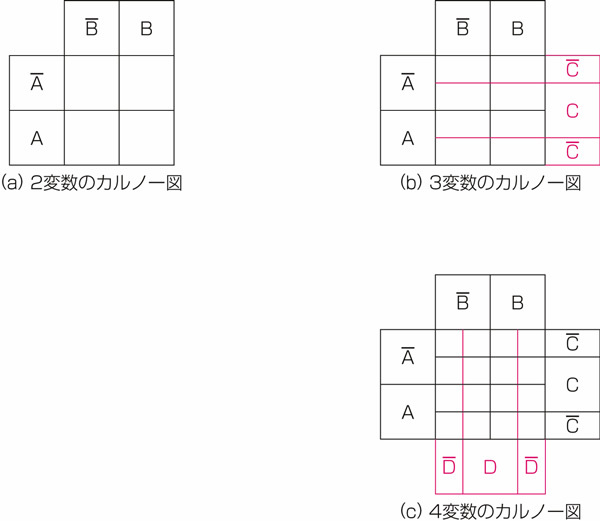
先ずは図26.2の（a）をご覧ください。これは2変数のカルノー図です。2変数AとBが、真と偽のそれぞれの値をとるすべての場合（場合の数=2×2=4）を網羅しています。この図に少し手を入れて3変数の場合のカルノー図を作ります。図26.2の（b）をご覧ください。赤で新しい線を加え、新しい変数Cを加えています。こうすることで、3つの変数が真偽のそれぞれの値をとるすべての場合（場合の数=2×2×2=8）が網羅されています。同様に4変数の場合を作成することができます。図26.2の（c）をご覧ください。赤い線で新しい変数Dの欄を加えました。すべての場合（場合の数=2×2×2×2=16）が網羅されていますね。

カルノー図の枠の書き方は、この他にも様々ありますが、このように2変数の場合をもとに書き加えて行く方法が覚える手間が少ないためおすすめです。

3変数の場合のカルノー図

次の3変数の論理式をカルノー図を使って簡略化してみましょう。

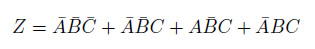
図26.3に簡略化の手順を示します。

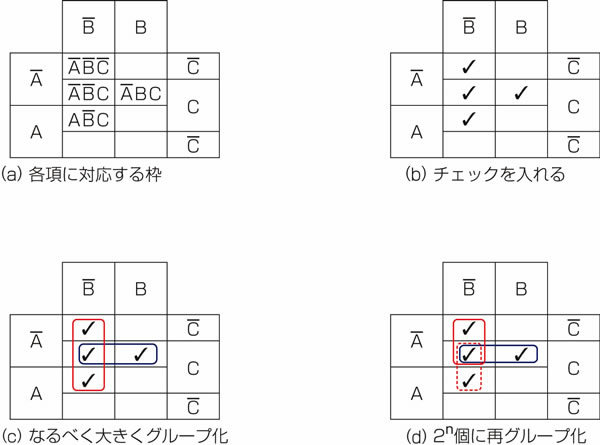
図26.3の（a）に、式の各項が対応するマスを示しました。対応するマスを見つけ、チェックを入れたところが図26.3の（b）です。前回までと同様になるべく大きな囲みでグループ化しましょう。すると図26.3の（c）のようになりました。

さて、ここで新しい手順を加えます。

カルノー図でチェックをグループ化する際、一つのグループに含まれるチェックの数は2ⁿ個でなければなりません。

つまり、一つのグループに含まれるチェックの数が、1,2,4,8,・・・になるようにするのです。図26.3の（c）の赤いグループは3つのチェックで一つのグループですから、2ⁿになっていません。このまま式化しようとすると、カルノー図のメリットが生かせません。そこで、グループに入るチェックの数を2か4にしなければなりません。今回の場合は、3つのチェックを2つずつに切り分けて図26.3の（d）のようにしました。グループの切り分けは、このように重複しても結構です。

さて、こうして切り分けた赤線、赤点線、青線のグループをそれぞれ式化し、論理和をとれば求める簡略化された論理式が得られます。

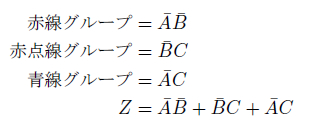
3因子ずつ4項あった式が2因子ずつ3項の式に簡略化されました。単純に考えれば、半分に簡略化できたのです。

4変数の場合のカルノー図

次の4変数の論理式をカルノー図を使って簡略化してみましょう。

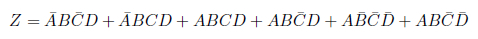
図26.4に簡略化の手順を示します。

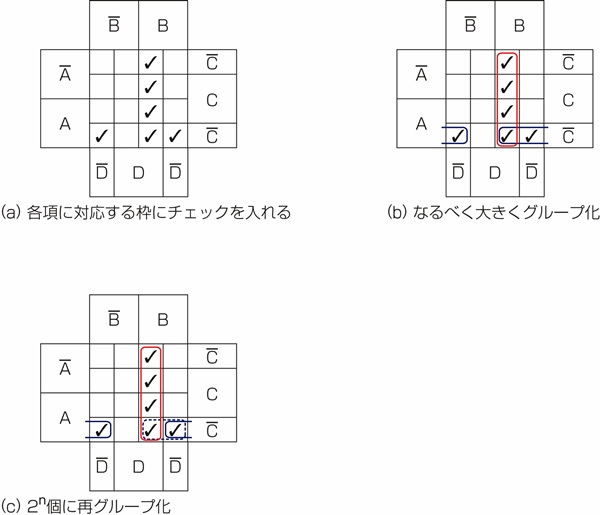
図26.4の（a）に、式の各項が対応するマスにチェックを入れたものを示しました。

カルノー図では、左右の境界どうし、上下の境界どうしは連続しているものと考えます。

上下、左右の境界どうしをつないでリングのように、切れ目がない図なのです。ですから、図の右端と左端にチェックがあれば、図の（b）のような囲み方ができるのです（※⁠）⁠。

最後に、一つのグループに含まれるチェックの数は2ⁿ個でなければならないというルールに従って、青い囲みを2つに分けます。図26.4の（c）のようになります。

さて、こうして切り分けた赤・青線のグループをそれぞれ式化し、論理和をとれば求める簡略化された論理式が得られます。

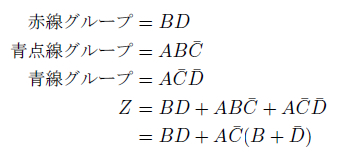
最初の式と比べると、大変に簡略化されました。公式に頼らず、たったこれだけの手間で得られるのですから、有り難いことです。

式変形やカルノー図による論理の整理は、プログラミングに応用すれば、プログラムコードの見通しを良くしたり、高速化に役立ち、論理回路設計においては論理素子数の削減に役立ちます。不可欠の知識・技術ですが、場合によっては論理の意図やプログラムの見通しを妨げる場合があります。式の整理にあたっては十分に注意しなければなりませんし、特にあやまった形の整理を行わないようにしなければなりません。プログラムが速く動いても間違っていては意味がないからです。式の整理を行う場合には、元々どんな式であったのか、ソースコード中に注釈として残しておくと良いでしょう。

※）

同様に、赤の囲みも、一番上と一番下にチェックがありますから、ぐるりと上下端の無い囲みを描いてもよいのです。

今回はここまで

今回は、3変数・4変数の場合のカルノー図の作成手順と利用方法を解説しました。例のごとく、次回の練習問題に取り組み、単に知識に終わらせず、スキルとして身につけましょう。