鋸（のこ）げんのう（金槌⁠）⁠、鉋（かんな⁠）⁠。大工道具には様々な種類があります。大きさの違いまで考えればきりがありません。釘にもたくさんの種類があります。普通に見かける釘は「丸釘」といいます。軟らかくて脆（もろ）い石膏ボードの打ち付けに使う釘は、特に細く長い専用の釘です。胴体に凹凸のついた「ねじ釘」というものもあり、これはいったん打ち込まれると抜くのがやっかいです。大工さんはこのような各種のくぎを工具箱に分類・整理しておき、必要に応じて選び、適材適所で釘を選択しています。

大工さんに限らず、たくさんのものを管理するためには、分類・選別・選択といった作業が日常的に行われます。そうしないと、いざ必要なものを選択するとき大変な目に遭うことでしょう。

情報の分類・選別・選択を、より厳密に効率よく表現する数学的な道具が、これから学ぶ「集合の数学」です。一見当たり前のことでも、集合の数学を活用して整理すると、そこに新しい発見をすることがあります。集合の数学を活用すると意外にも大きなメリットがあるのです。

この記事が、読者の皆さんの問題解決効率を高め、新たな発見に役立てばよいなと期待しています。

改めて「集合」ってなんですか？

集合とは、数学的にはいくつかの「もの」からなる「集まり」のことです。あまりに抽象的すぎて、わかったような、わからないような、狐につままれているような気になるかもしれません。先ずは「集合の数学を学ぶことで、日頃何気なく行っている「ものの集まり」の表現や操作をきっちり出来るようになる」というメリットがあると思ってください。

一つ例を示しましょう。図29.2に一つの図を示します。この図は直感的で何も数学的に見えないかもしれません。四角と丸が無造作に書かれています。

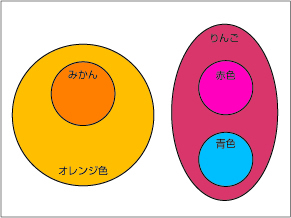
この図の書き方やルールについてはやがてきちんと学ぶものとして、ぱっと見て、この図が「みかんは全てオレンジ色です。」「⁠りんごには赤色のものと青色のものがあります。」ということがきっちり表されていると納得出来るでしょうか？きっと納得できると思うのです。疑問を差し挟む余地は無いと思います。

こんな図、描くまでもないんじゃない？というご指摘はごもっとも。しかしこれはお話を簡単にするための例ですからご容赦を。こんな簡単な図であっても、図にしたからこそ得られるメリットがあるのです。それは「ものごとをキッチリ表現できる」こと、そして「図を書いた人が、当初想定していなかった事実が図に表れる」ことなのです。そんな夢みたいなことがあるの？そう、あるのです。この度の場合はそれほど重要な事実ではありませんが、確かに先ほどの文章では意図していなかったことが図から読みとれるのです。

例えばこんな具合です。

• 「みかんはりんごではありません。」「⁠りんごはみかんではありません。」

いえいえ、怒らないでください。しかし、確かにさっき述べた文章の意図には無かったものでしょう？当たり前かもしれませんが、当初は思いもしなかった事実をはっきりとこの図が言い表しているのです。

更に、このように図を読むことも出来ますよ。

• 「赤色や青色のみかんはありません。」「⁠オレンジ色のりんごはありません。」

もし、現実世界の事実と図示した事実が矛盾するようであれば、新発見をしたのかもしれませんし、自分の考えの誤りに気づかされたのかもしれません。数学によって自分の中に他者の目を得たとも言えます。すばらしいことだと思いませんか？

集合の数学とプログラミング言語

この集合という数学の道具は、コンピュータ・プログラマにとって、たとえそれと意識しなくとも大変身近なものです。例えば、プログラミングを学ぶ人は、データの集まり（集合ですね）を取り扱うために、配列という仕組みを早晩学びます。配列には、数値を格納したり、名前（文字）を格納したりできます。格納した値を並べ替えたり、一番大きいものをさがしたりします。格納する値の数が多ければ多いほど、コンピュータはその真価を発揮します。

配列というプログラミング言語の仕組みは、少々物足りなく感じることがあります。あるとより便利な機能はJava言語ではコレクションクラスというもので備えています。ただ、このコレクションクラスは大変シンプルで、集合の数学を活かすにはまだまだプログラマが付け加えなければならない機能が残されています。では、どんな機能があると便利なのでしょうか。次回からはそのようなことも学びましょう。

集合論（Set Theory）を作ったカントール（g.Cantor,1845-1918）は次のように集合を言い表しています。

集合とは、われわれの直観または思考の対象で、確定していて、互いに明確に区別されるものを一つの全体としてまとめたものである。

（寺阪秀孝編著『現代数学小辞典』ブルーバックスB325（講談社,1977）p.44）

この表現と、私たちが日常で大量のデータを取り扱うことの間にはギャップがあります。なぜなら、数学的に厳密に表現される集合は、集合に含まれるものが「互いに明確に区別されるもの」であるからです。しかし実際に私たちの取り扱うデータは、重複があったり、曖昧なものであったりします。すべての場合において、集合に含まれるものを厳格に区別して取り扱うことは、現実的に手間と効果が釣り合わないものです。これは、現実世界のデータ処理にコンピュータを用い、集合の数学を活かす場合に勘案すべきことが少なくないことを示唆しています。

しかし、集合の数学を知った上であるからこそ、現実にある「だぶり」や「曖昧さ」を含んだデータを取り扱うとき、ある処理のためにどの程度の厳密さを持ち込む必要があるのか、といった判断も出来るのです。ほとんどの身近な事例の場合、意識せずそれを行っているのですが、大量のデータを業務として間違いなく処理していくためには、集合の数学の助けを借りることになるのです。SQL[1]のSELECT文を使うときなどは、まさにそういう場合です。SQLのSELECT文では、AND、OR、NOTといった演算をデータの取捨選択に用います。これまでに学んだ論理の数学の知識がここでも生きるのです。

簡単な例を一つ。年賀状の名簿には、名簿の持ち主の好みの問題ですが、過去の住所も一応残しておいたりします。実家の住所であったり、互いに交流の会った頃の思いでの記録であったりするからです。集合の要素とは、本来「確定していて」「⁠明確に区別される」ものなのに、ある人物に関するデータが複数あるのですから好ましくありません。年賀状を作成する場合には、最新の住所宛に一通出せばよいのです。そこで、名簿に何らかの印を付けておいて[2]年賀状作成時に取捨選択するのです。まさしくこれは、集合の数学（分類・選別・選択）を適用しているのです。

これからの連載で学ぶこと

これからの連載では、集合の数学で用いる記号や公式の確認、配列やコレクションクラスといった集合の数学を具体的に活用するためのJava言語の仕組みを紹介していきます。

集合の数学を、効率のよいデータ処理に活かしましょう。