フラクタル図形というものがあります。全体は緻密で幻想的な模様なのですが、この図形を支配するルールはいたってシンプルです。基本となる図形が一つ。次の図形になるための簡単なルールがひとつ。基本図形とルール適用という小さな部分の連続が、全体として幻想的な模様を形作ります。仏教曼荼羅画を眺めていると同じような感覚におそわれます。お寺や神社の建物の造りは、恐らくそのような影響を受けているのでしょう。細かな細工の集まりですが、全体として大きなバランスを保っています。欧米のプログラマは禅を学ぶ人が少なくないと聞きました。ストレスの多い職業ですから、無の境地を求めてのことかもわかりませんが、仏教の持つ無限集合的な宇宙観に惹かれているのかもしれません。
今回学習する集合の概念にも、部分や無といったものが登場しますが、それらは得体の知れない哲学的な概念ではなく、シンプルで明確な数学的概念です。ことばそのままに受け入れていただければ良いでしょう。それこそ、禅を行っているような心境で。
図33.1 複雑な寺院の建築も、シンプルな部分の集合

部分集合とは
部分集合とは、ある集合Aの要素の一部、あるいは全体を取り出した集合のことです。集合の数学記号では、集合Aと部分集合Bの関係を次のように書きます。

混乱しやすいので再度確認します。ある集合が別の集合の部分集合であると言われる場合、全く同じ集合のこともあるということを忘れないようにしましょう。上述の場合ならば、「集合Bは別の集合Aから取ってきたものなのだ」ということを「部分集合である」と言い換えているです。
集合Bは集合Aの一部をとってきたのだとします。一部と言うことは、集合Bには入っていない要素が集合Aにあるということです。そのような場合、集合Bは集合Aの真部分集合であるといいます。数式で書き表すと次のようになります。

単に部分集合であると表現されているとき、二つの集合は同じ集合である事もあるし真部分集合であることもあります。ですから、集合に含まれる要素が明確であるときは、「真部分集合」か「等しい集合」と表現すると良いでしょう[1]。
具体的に集合とその要素を式と図で書き表してみましょう。
 図33.2 部分集合、真部分集合
図33.2 部分集合、真部分集合
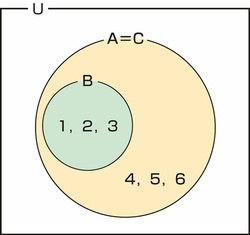
こうすると、集合Cは式33.8のように、部分集合ともいえますし、式33.9のように等しい集合ともいえます。どの式を用いるかは、文脈に寄るのです。
空集合とは
空集合とは、要素を一つも持たない集合のことで記号φ(ファイ)で表します。空集合は、集合の演算で当てはまる要素がなかった場合の結果として得られます。記号φを覚えておきましょう。
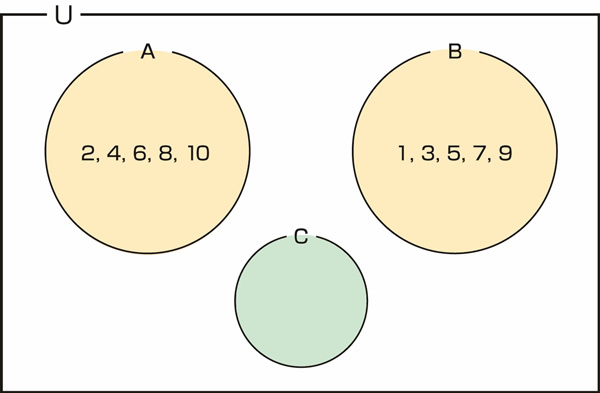
例えば、自然数の集合内において、10以下の偶数の集合Aと、10以下の奇数の集合Bの共通する要素を集めた集合Cを考えてみましょう。題意から、一致する要素はありません。ですから集合Cは空集合.です。
 図33.3 空集合
図33.3 空集合
Java言語と部分集合・空集合
次のような場合を考えてみましょう。
- 「住所録データから、今年年賀状を出す相手を抽出する。」
ここで、年賀状データをA、今年年賀状を出す相手のリストをBとしましょう。すると、BはAの一部かも知れませんし、全部かもしれません。このような状況はA⊇Bと書き表せます。
もし、喪中のはがきが届いており、年賀を出さない相手がわかっていれば、確実にAに含まれていてもBに含まれない人があるわけです。このような状況はA⊃Bと書けます。
コンピュータでデータ処理をする場合には、「単に年賀状を出す相手をこれから決める」という段階は、部分集合を得るために住所録データをそのまま複製することだと言えます。喪中の人が明らかになって、さあ年賀状を作成するという段階の名簿を得るという段階は、真部分集合を得るために住所録データの取捨選択を行ったことにあたります。真部分集合である「今年年賀状を送る人のリスト」は、データ処理を行う前は空かもしれません[2]。もし空であれば、その時点でのその集合は空集合であるといえます。
これらの処理は、加減乗除のようなシンプルな演算子で実行できることではなく、データの格納された配列やArrayListを一つ一つ条件に照らし合わせて取捨選択するという地道な処理が必要となります。データ量が膨大な場合はJava言語でゼロからプログラムを作るのではなく、データベースシステムを利用する方がよいでしょう。
今回はここまで
いかがでしたか?改めて語句を眺めてみて、それらの語句の表すことを無意識に、自然に行っていることが納得できますか?まだ今の段階では語句の確認とプログラミングとの対応付け程度ですから有難味が感じられないかもしれません。しかし、物事を明確に表現することのメリットは必ずありますので、その方法である集合の数学の各項目について、おざなりにすることなく一つ一つチェックしておいてくださいね。レゴのブロック一個では楽しい遊びはありませんが、たくさん集まれば車でも宮殿でも作れるようなもの、数学も積み上げてこそ役に立ちますから。
世の中にはデータベース処理用の優れたソフトウエアやライブラリがあります。なるべくそのようなものを使うべきだとはわかっていても、小さなデータを「ちょっと」取り扱う場合には、自前で処理するコードを組んだ方が良い場合が多々あります。次回はそんな演習問題を用意しました。簡単なようで意外と煩雑ですから、是非とも取り組んでみてください。










