ヤスリがけの習得は、
行列の数学の学習も、

一行だけ、一列だけの行列=ベクトル
行列の中でも一行だけ、
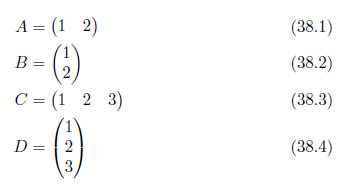
具体的な例にあてはめてみましょう。例えば、
例えばあるベクトルXがリンゴの数とミカンの数を表すものだとします。
仮にX=
リンゴが2、
空間ベクトル![]() の成分が
の成分が
式38.
ベクトルの加算・減算
さて、

この式は、
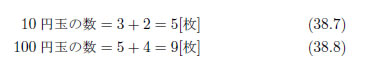
もちろん、
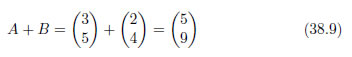
加算はこのとおりです。減算も同様に行うことが出来ます。
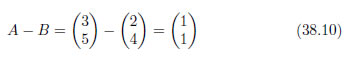
ベクトルの加算・
ベクトルをJava言語で表現しよう
ここまでのところを、
さあ、
問題:ベクトルの加算を行う関数を作りましょう。
整数を成分として持つベクトルの加算メソッドを、
引数として渡された配列やArrayListの要素数から次元数を判断し、
関数はAddMatrixのように呼び出しましょう。行列Aと行列Bの和を行列Cに格納してください。
配列版はaAddMatrixという関数にしてください。
解説
先に配列版を示します。ベクトルの加減算は最もシンプルで考えやすい題材です。プログラミングを始めたばかりの人にとっては、
///サンプルコード
//行列(ベクトル) の和をとる。配列版。
//filename : HairetsuDeMatrixAdd.java
class HairetsuDeMatrixAdd {
static final int MAX_LENGTH = 255; //配列長の最大値
public static void main(String[] args) {
int a[] = {1,2,3,5,8}; //ベクトルa
int b[] = {2,4,5,7,9}; //ベクトルb
// int b[] = {2,5}; //要素数が異なると加算できない
int c[] = new int[MAX_LENGTH]; //ベクトルc
//C = A + B
vAddMatrix(a,b,c);
//結果表示
for( int i = 0 ; i < a.length ; ++i ){
System.out.println("a["+i+"] + b["+i+"] = c["+i+"]");
System.out.println(a[i] + " + " + b[i] + " = "+ c[i]);
}
}// end of main
static void vAddMatrix(int a[], int b[], int c[]){
if (a.length == b.length){
//加算可能
for( int i = 0; i < a.length ; i++){
c[i] = a[i] + b[i];
}
} else {
//加算不能
System.out.println("加算できません");
System.exit(0);
}
}
}// end of class HairetsuDeMatrixAdd次にArrayList版を示します。ベクトルの加算と言うことに関しては、
//サンプルコード
//行列(ベクトル)の和をとる。ArrayList 版。
//filename : ArrayListDeMatrixAdd.java
import java.util.ArrayList;
class ArrayListDeMatrixAdd {
public static void main(String[] args) {
//ベクトルA の宣言と初期化
ArrayList<Integer> A = new ArrayList<Integer>();
int a[] = {1,2,3,5,8};
for (int i=0 ; i < a.length ; ++i ) A.add( a[i] );
//ベクトルB の宣言と初期化
ArrayList<Integer> B = new ArrayList<Integer>();
int b[] = {2,4,5,7,9};
// int b[] = {2,5}; //要素数が異なる場合は加算できない
for (int i=0 ; i < b.length ; ++i ) B.add( b[i] );
//ベクトルC の宣言
ArrayList<Integer> C = new ArrayList<Integer>();
//C = A + B
aAddMatrix(A,B,C);
//結果表示
for( int i=0 ; i < A.size() ; ++i ){
System.out.println("A("+i+") + B("+i+") = C("+i+")");
System.out.println(A.get(i)+" + "+B.get(i)+" = "+C.get(i));
}
}// end of main
static void aAddMatrix(ArrayList<Integer> A, ArrayList<Integer> B,
ArrayList<Integer> C){
if (A.size() == B.size()){
//加算可能
for( int i = 0; i < A.size() ; i++){
C.add( A.get(i) + B.get(i) );
}
} else {
//加算不能
System.out.println("加算できません");
System.exit(0);
}
}
}// end of class HairetsuDeMatrixAdd今回はここまで
Java言語を用いて、



