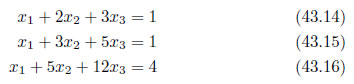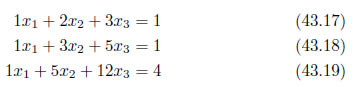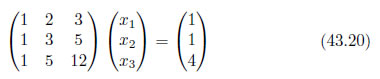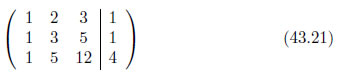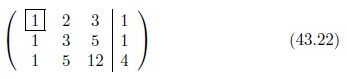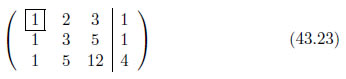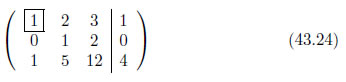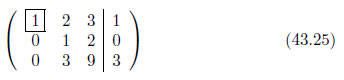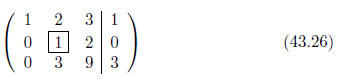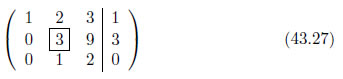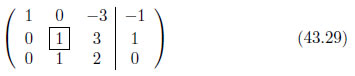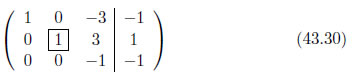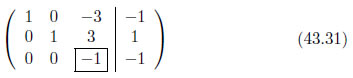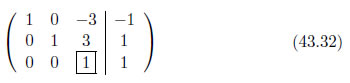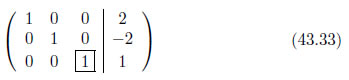柔道の技は派手さがありません。映画に登場するカンフーや空手のように、ジャンプしたり、宙返りすることはありません。柔道の技は、バランスの崩し合いです。前後左右、そして上下へ相手のバランスを崩すのが技の目的です。人間は、いったんバランスを崩してしまったら、後のコントロールが効きません。倒すも投げるも相手のなすがままです。前後の移動、足払い、手で引く、押す。柔道の技はこれらの組合せです。大変シンプルなのですが、奥の深い世界です。
さて、行列の数学を用いて連立一次方程式を解くという今回の学習内容は、大変シンプルな操作によって成り立っています。使用しているのは単純な加減乗除と式の並べ替えだけです。一定のわずかな約束に従って式の操作を繰り返していくと、あら不思議、気がつくと解が手に入ってしまいます。技はシンプルな操作の組合せ。門外漢からみると、まるで魔法のように見えてしまうのですが、実はとても単純なことを、几帳面にこなしているだけなのです。
図43.1 技とは地味で単純な操作の組合せ

逆行列
逆行列[1]とは、元となる行列との積が単位行列になる正方行列のことです。逆行列に変換できる行列は正則[2]である、また正則行列[3]であるといいます。

式43.3のような正方行列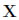 があるとき、
があるとき、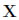 を
を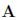 の逆行列といい、
の逆行列といい、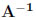 と書きます。
と書きます。
式43.3は、ある行列に逆行列が存在すると言うことは、行列で表現された方程式の解を求めることが出来ることを表しています。
連立一次方程式を行列の数学で解く
連立一次方程式は、構造物の強度計算や流体のシミュレーション等、科学技術計算に不可欠な手段です。未知数が少なければ手で計算することも出来ますが、通常、科学技術計算では多数の未知数があり、手で計算して解を求めることは現実的に不可能なものがほとんどです。そこで、今回学習するような方法を用いて、コンピュータに解を求めさせるのです。これは、コンピュータが不可能を可能にした技術の好例です。
一般的に、連立一次方程式は次のように書くことが出来ます。
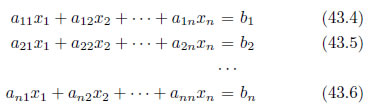
x1・・・xnは未知数、nは未知数の個数(元数)、b1・・・bnは定数を表しています。連立方程式に含まれるa11・・・annは、方程式の係数です。これらを行列を用いて表現すると、次のように書き表すことが出来ます。

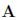 は係数行列、
は係数行列、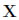 は解ベクトル、
は解ベクトル、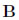 は定数項ベクトルと呼び、具体的には次のような行列です[4]。
は定数項ベクトルと呼び、具体的には次のような行列です[4]。
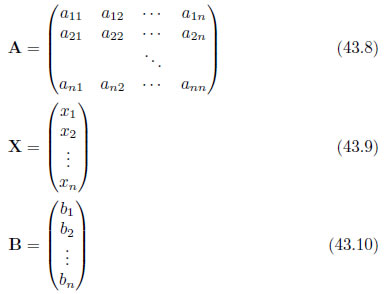
式43.7の左辺を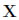 だけになるよう式変形すると、それはすなわち未知数の行列
だけになるよう式変形すると、それはすなわち未知数の行列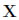 の値を決定できたと言うことになります。式の変形手順は、次のとおりです。
の値を決定できたと言うことになります。式の変形手順は、次のとおりです。

以上のことから、行列を用いて連立一次方程式を解くためには、係数行列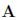 の逆行列
の逆行列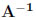 を求め、定数ベクトル
を求め、定数ベクトル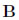 との積を計算すれば良いことがわかります。
との積を計算すれば良いことがわかります。
ところが、逆行列を求めてから解を計算するアルゴリズムは効率が良くありません。そこで、できるだけ少ない手数で式43.7から式43.13への変形を行う方法が数多く考案されました。そのうちの一つが、次に紹介する方法です。
ガウス-ジョルダン法
ガウス-ジョルダン法[4]は、数ある連立一次方程式の解法の中でも特に手順がシンプルです。実際にはより少ない計算手順で解を求めることが出来る方法があります[5]ので、ガウス-ジョルダン法が実際のアルゴリズムとして利用されることは多くないようです。しかし、プログラミングの入門段階では、適度な難易度の課題であると思われます。
では、次の連立一次方程式の解をガウス-ジョルダン法を用いて計算してみましょう[6]。
問題を整理する
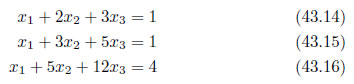
式の整理
行列の式に変換するために、係数を明確にします。
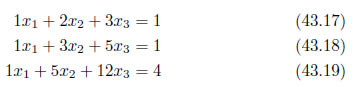
行列の式で表す
行列の式で表します。
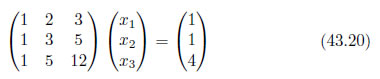
ガウス-ジョルダン法を適用しやすい書式に書き直す
式43.20を次のように書き直します。
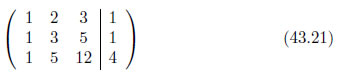
1行目
ピボットの選択
1行目・1列目の値に注目します。この値から行列の右下まで、右下がりの対角線上にある値のことをピボット[7]といいます。ピボットは、その列にある値の絶対値の最大値を選ぶべきです[8]。最大値でない場合には、最大値のある行と入れ替えます。
ピボットの列の値をみると、全て1です。ですから、この値はピボットとして適していると言えます。今回は列の交換は必要ありません。
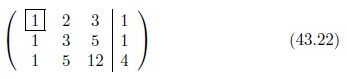
ピボットを1にする
ピボットの値が1になるように操作します。式43.20の1行目の式の両辺を、ピボットの値で除算します。今回はピボットが1ですから、式に変化がありません。ピボットが1以外の場合は式の係数・定数に変化が生じます。しかし、両辺を同じ値で除算するのですから、式の意味は不変です。
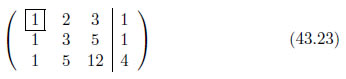
掃き出し
ピボットのある列の各要素の値がゼロになるように式を操作します。この操作を掃き出し[9]といいます。式43.23の2行目・1列目をゼロにするためには、1行目の全要素に2行目・1列目の値を乗算し、その後に2行目から引きます。今回、2行目・1列目の値は1です。1を1行目に乗算し、2行目から引くと次のようになります。
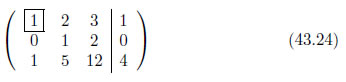
同様に、3行目・1列目もゼロになるように操作します。
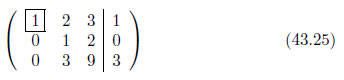
以上の操作がワンセットです。1行目・1列目のひとつ目のピボットに関する操作が終了しました。ふたつ目のピボットに関する操作に移ります。
※9)
Sweeping
2行目
ピボットの選択
ふたつめのピボット、2行目・2列目を選択します。現状のピボットの値は1です。
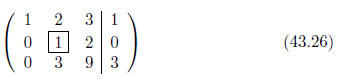
このピボットの位置より下を見ると[10]、次の行に3があります。これが最大値です。3行目と2行目を入れ替えます。
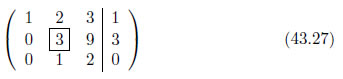
ピボットを1にする
ピボットの値が1になるように操作します。現在のピボットの値でピボットのある行の値を全て除算します。

掃き出し
ピボットのある列の各要素の値がゼロになるように式を操作します。この掃き出し操作は、現在のピボットのある行より上の行についても全て行います。1行目の現在のピボットのある列の値、1行目・2列目の値は2ですから、2行目に1行目・2列目の値を乗算し、1行目から減算します。
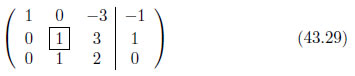
3行目の現在のピボットのある列の値、3行目・2列目の値は1ですから、2行目に、3行目・2列目の値を乗算し、3行目から減算します。
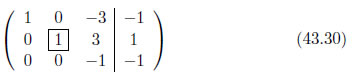
これで第2セットが終了です。ふたつめのピボットに関する処理が終了しました。次が最後のピボットです。
3行目
ピボットの選択
ピボットの選択を行うのですが、これ以上下に行がありませんので自然と現在の行、そして現在のピボットの値を用いることになります。
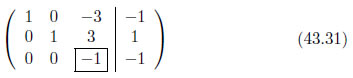
ピボットを1にする
ピボットの値が-1ですから、-1で3行目の全ての要素を除算します。
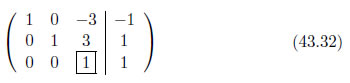
掃き出し
ピボットのある列の各要素の値がゼロになるように式を操作します。1行目・3列目をゼロにするために、3行目の全ての要素に-3を乗算したもので一行目を減算します。2行目・3列目をゼロにするために、3行目の全ての要素に3を乗算したもので2行目を減算します。
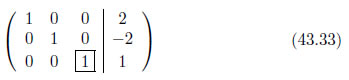
以上で全ての操作が終了しました。行列43.33の右端の列が解を表しています。
解

ガウス-ジョルダン法の計算手順の計算手順がつかめたでしょうか。解説を読むだけではなく、同じ問題で結構ですから、紙に書き写して手順を追ってみましょう。そうすればしっくり納得出来るはずです。
今回はここまで
行列の数学を用いて連立一次方程式の解を求める仕組みを紹介しました。最初のうちは、方程式の解を求めるなんて、複雑な状況判断を必要としそうで、とてもプログラムに出来そうもない、と思われたのではないでしょうか。しかし、ガウス-ジョルダン法の計算手順に従うと、なんともシンプルな手順を繰り返すうちに、気がつくと解が得られていることに驚きさえ感じたことでしょう。
次回はこのガウス-ジョルダン法の計算手順をプログラムにして実行しましょう。恐れることはありません。道は用意しておきますので。


![]() があるとき、
があるとき、![]() を
を![]() の逆行列といい、
の逆行列といい、![]() と書きます。
と書きます。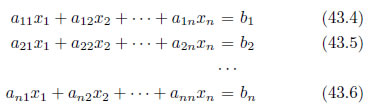

![]() は係数行列、
は係数行列、![]() は解ベクトル、
は解ベクトル、![]() は定数項ベクトルと呼び、
は定数項ベクトルと呼び、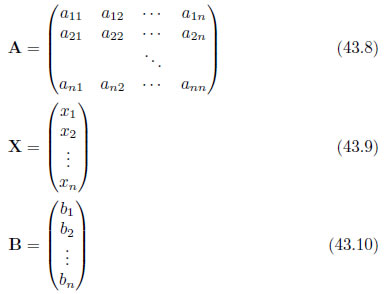
![]() だけになるよう式変形すると、
だけになるよう式変形すると、![]() の値を決定できたと言うことになります。式の変形手順は、
の値を決定できたと言うことになります。式の変形手順は、
![]() の逆行列
の逆行列![]() を求め、
を求め、![]() との積を計算すれば良いことがわかります。
との積を計算すれば良いことがわかります。