柔道の
今回、

問題 ガウス-ジョルダン法の計算手順を利用して逆行列を求めましょう
ガウス-ジョルダン法で逆行列が得られる仕組み
ガウス-ジョルダン法の計算手順を利用して、
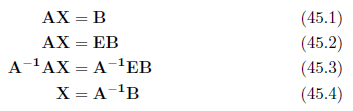
式45.
両辺に逆行列を掛けると
以上のことから、
サンプルコードを完成させましょう
サンプルコード未完成版に処理の大筋と、
(A)から(C)
3つの箇所は、
このとき、
(D)
新しく作るinverseMatrixメソッドに含まれています。このメソッドは、
少々長いサンプルのソースコードですが、
//サンプルコード
//Gauss-Jordan Elimination(ガウス-ジョルダン法)で
//逆行列を求める。配列版。
//filename : Sample_inverseMatrix.java
class Sample_inverseMatrix {
public static void main(String[] args) {
//---------------------------------
//テスト用のデータを準備
//---------------------------------
//逆行列が得られる場合
double a[][] = //行列A
{ { 0, 1, 2 },
{ 1, 2, 1 },
{ 1,-1, 1 } };
double inv_a[][] = //A の逆行列の計算結果
{ { 0, 0, 0 },
{ 0, 0, 0 },
{ 0, 0, 0 } };
double ROH[][] = //望まれる結果
{ {-0.5, 0.5, 0.5 },
{ 0, 0.3333333333333333, -0.3333333333333333 },
{ 0.5,-0.16666666666666666, 0.16666666666666666} };
// { { -1/2, 1/2, 1/2 },
// { 0, 1/3, -1/3 },
// { 1/2, -1/6, 1/6 } }; //のことである。
// 望まれる結果の値は、関数電卓で計算した結果を使用
//正則でない場合
double a2[][] = //行列A2
{ { 1, 0, 3 },
{ 2, 3, 4 },
{ 1, 3, 1 } };
//---------------------------------
//GJE テスト用のデータを準備
//---------------------------------
//一意な解が得られる場合
double gje_a[][] = //係数行列A
{ { 0, 1, 2 },
{ 1, 2, 1 },
{ 1,-1, 1 } };
double gje_b[][] = //定数ベクトルB
{ { 3 },
{ 6 },
{ 3 } };
double gje_x[][] = //解ベクトルX
{ { 0 },
{ 0 },
{ 0 } };
double gje_ROH[][] =//望まれる解ベクトル
(ResultOfHope)
{ { 3 },
{ 1 },
{ 1 } };
//---------------------------------
//逆行列を求めます
//---------------------------------
System.out.println("Inverse Matrix Test Start");
//Test 1
//与えた行列は正則で、期待される解をきちんと返すので、
//特別な出力はないはず。
test_isIM_DoRight(a,"a",inv_a,"inv_a",ROH,"ROH",true);
//Test 2
//与えた行列は正則ではないので、条件に指定したとおり
//false を返すので特別な出力はないはず。
test_isIM_DoRight(a2,"a2",inv_a,"inv_a",ROH,"ROH",false);
System.out.println(" Test Done");
//---------------------------------
//ガウスジョルダン法を実行します
//---------------------------------
System.out.println("Gauss-Jordan Elimination Test Start");
//Test 1
//計算結果が望んだ解と等しい。isDoRight_ROH もtrueを指定。
//正しく終了し、特別なメッセージを出力しないはず。
test_isGJE_DoRight(gje_a,"gje_a",gje_b,"gje_b",
gje_x,"gje_x",gje_ROH,"gje_ROH",true);
System.out.println(" Test Done");
}// end of main
/*
* test_isIM_DoRight
* 目的 : inverseMatrix メソッドのテスト
* 引数 : a 係数行列
* b 定数ベクトル
* x 解ベクトル
* ROH 解ベクトルの正解
* isDoRight_ROH 正しく解が得られたか。
* valName* 引数に渡した変数名
* 戻り値: boolean
* inverseMatrix の結果と
* isDoRight の結果が等しいときに真を返す。
* inverseMatrix が真、
* isDoRight の値が真であっても、
* 望まれる解が得られなかった場合は偽
*/
static boolean test_isIM_DoRight(double a[][],String valNameA,
double inv_a[][],String valNameInvA,
double ROH[][],String valNameROH,
boolean isDoRight_ROH){
double result[][] = new double[a.length-1][a[0].length-1];
boolean IMresult = inverseMatrix(a,inv_a);
if (IMresult == isDoRight_ROH) {
if (IMresult == false){
//System.out.println(" 望んだ結果であるが、"+
// "逆行列は得られませんでした。"
// + valNameA + valNameX);
return true;
}
if (isMatrixEqualsDouble(inv_a,ROH) == true) {
//System.out.println(" 望んだとおりの結果であり、" +
// "関数の返した答えは正しい値でした。"
// + valNameA + valNameX);
return true;
} else {
System.out.println(" 関数は真を返しましたが、" +
"正しい解ではありませんでした。"
+ valNameA + valNameROH);
showMatrix(inv_a);
return false;
}
} else {
System.out.println(" 関数が望んだ"+isDoRight_ROH+
"を返しませんでした"
+ valNameA + valNameROH);
return false;
}
}// end of test_isIM_DoRight
/*
* test_isGJE_DoRight
* 目的 : isGJE_DoRight メソッドのテスト
* 引数 : a 係数行列
* b 定数ベクトル
* x 解ベクトル
* ROH 解ベクトルの正解
* isDoRight_ROH 正しく解が得られたか。
* valName* 引数に渡した変数名
* 戻り値: boolean
* evokeGaussJordanElimination の結果と
* isDoRight の結果が等しいときに真を返す。
* evokeGaussJordanElimination が真、
* isDoRight の値が真であっても、
* 望まれる解が得られなかった場合は偽
*/
static boolean test_isGJE_DoRight(double a[][],String valNameA,
double b[][],String valNameB,
double x[][],String valNameX,
double ROH[][],String valNameROH,
boolean isDoRight_ROH){
boolean GJEresult = evokeGaussJordanElimination(a,b,x);
if (GJEresult == isDoRight_ROH) {
if (GJEresult == false){
//System.out.println(" 望んだ結果であるが、"+
// "一意な解は得られませんでした。"
// + valNameA + valNameB + valNameX);
return true;
}
if (isMatrixEqualsDouble(x,ROH) == true) {
//System.out.println(" 望んだとおりの結果であり、" +
// "関数の返した答えは正しい値でした。"
// + valNameA + valNameB + valNameX);
return true;
} else {
System.out.println(" 関数は真を返しましたが、" +
"正しい解ではありませんでした。"
+ valNameA + valNameB + valNameX + valNameROH);
showMatrix(x);
return false;
}
} else {
System.out.println(" 関数が望んだ"+isDoRight_ROH+
"を返しませんでした"
+ valNameA + valNameB + valNameX + valNameROH);
return false;
}
}// end of test_isGJE_DoRight
/*
* evokeGaussJordanElimination
* 目的 : 引数で与えた行列について
* Gauss-Jordan Elimination を実施する。。
* 引数 : a[][] 倍精度実数型の二次元配列。係数行列。
* : b[][] 倍精度実数型の二次元配列。定数ベクトル。
* : x[][] 倍精度実数型の二次元配列。解ベクトル。
* 戻り値 : boolean 一意な解が得られれば真
* 一意な解が得られなければ偽を返す。
* 引数に与えた変数に問題があった場合も偽を返す。
*/
static boolean evokeGaussJordanElimination(
double a[][], double b[][], double x[][]){
//解ベクトルをゼロクリア
for(int row = 0; row < a.length; ++row) x[row][0] = 0;
//係数行列、定数・解ベクトルの次元数は適切か
if ( isSquareMatrixDouble(a) &&
(a.length == b.length) &&
(a.length == x.length) ){
//引数に与えた変数に問題なし。
for (int k=0; k < a.length; ++k){
//k は現在注目しているピボット位置
regulatePivot(a,b,k); //ピボットの調整
if (a[k][k] == 0){
//ピボットがゼロのとき、正則ではない。異常終了
return false;
} else {
//ピボットの値が正常なので掃き出し実行。
doSweep(a,b,k);
}
}// of for k
//ここまで来たと言うことは、正しく計算が終了しているということ。
for(int row = 0; row < a.length; ++row) x[row][0] = b[row][0];
} else {
//引数に与えた変数に問題がある。
return false;
}
//ここまで到達したということは成功
return true;
}// end of evokeGaussJordanElimination
/*
* isMatrixEqualsDouble
* 目的 : 引数で与えた二つの行列が等しいか
* 引数 : a[][] 倍精度実数型の二次元配列。
* : b[][] 倍精度実数型の二次元配列。
* 戻り値 : boolean 等しい行列であるなら真を返す。
*/
static boolean isMatrixEqualsDouble(double x[][], double ROH[][]){
if ( (x.length == ROH.length) ){
for (int row = 0; row < x.length; ++row){
if (x[row].length != ROH[row].length) return false;
for (int col = 0; col < x[row].length; ++col){
if (x[row][col] != ROH[row][col]){
//Value not equal
return false;
}
}
}
return true;
} else {
//Matrix is not equal
return false;
}
}// end of isMatrixEqualsDouble
/*
* isSquareMatrixDouble
* 目的 : 引数に与えた行列を表す配列が、正方行列かどうか判定する。
* 行数と一行に入っている要素数が等しいか確認する。
* 引数 : m[][] 判定する行列を表す倍精度実数型の二次元配列
* 戻り値 : boolean 正方行列なら真
*/
static boolean isSquareMatrixDouble(double m[][]){
int row = m.length; //行数取得
int cul = m[0].length; //一行目の要素数(列数)の取得
boolean result = true;
if (row == cul) {
for (int i = 0 ; i < row ; ++i ){
if (cul == m[i].length){
//列数は妥当である。
} else {
//列数が妥当ではない。
result = false;
break;
}
}
} else {
result = false;
}
return result;
}// end of isSquareMatrixDouble
/*
* showMatrix
* 目的 : 引数で与えた行列の全ての要素を表示する。
* 引数 : m[][]
*/
static void showMatrix(double m[][]){
for (int row = 0; row < m.length; ++row){
for (int col = 0; col < m[0].length; ++col){
System.out.print(m[row][col] + " ");
}
System.out.println();
}
}// end of showMatrix
/*
* regulatePivot
* 目的 : 係数行列のピボット値が適正になるように調整する。
* 具体的には、現在注目しているピボットのある列について、
* 最も大きな数値のある行と、現在のピボット行を交換する。
* 引数 : a[][] 係数行列。
* : b[][] 定数配列。
* : k 現在注目しているピボット位置
*/
static void regulatePivot(double a[][],double b[][] ,int k){
double max = Math.abs( a[k][k] );
double temp = 0;
int rowOfMaxPivot = k;//最大のピボット候補値の格納された行の値
if(k != (a.length - 1)){//最終行でなければ続きを実行
for (int row = k+1; row < a.length; ++row){
//ピボット行の次の行から
if( Math.abs(a[row][k]) > max ){//より大きな値を見つけて
max = Math.abs(a[row][k]);//最大値として保管し
rowOfMaxPivot = row;//その行が何行目か保管しておく。
}
}
}
if(rowOfMaxPivot != k){
//最大値のある行が、現在注目しているピボットのある行でなければ
//最大値のある行と、現在のピボット行とで値の交換
//現在のピボットのある列を含めて右側の値について交換を実施。
for (int col = k; col < a[0].length; ++col){
temp = a[k][col];
a[k][col] = a[rowOfMaxPivot][col];
a[rowOfMaxPivot][col] = temp;
}
// ここから 目的のコードを加えましょう。
// (A)
// ここまで
}
}
}// end of regulatePivot
/*
* doSweep
* 目的 : 掃き出し処理。
* 引数 : a[][] 係数行列。
* : b[][] 定数配列。
* : k ピボット位置
*/
static void doSweep(double a[][],double b[][],int k){
double pivotVal = a[k][k]; //掃き出し前のピボット値を保持
double pivotColVal = 0; //これから掃き出しを行う行のピ
//ボット列の値を保持しておく。
//ピボット値のある行の各要素を、ピボット値で割る。
for( int col=k; col < a[0].length; ++col)
a[k][col] = a[k][col] / pivotVal;
// ここから 目的のコードを加えましょう。
// (B)
// ここまで
//全ての行で、ピボット位置以外のピボット列の値をゼロにする。
//その副作用として、ピボット列以外の要素同士も減算を行う。
for( int row = 0; row < a.length; ++row){
pivotColVal = a[row][k];
if( row != k ){
for( int col = k; col < a[0].length; ++col)
a[row][col] = a[row][col] - pivotColVal * a[k][col];
// ここから 目的のコードを加えましょう。
// (C)
// ここまで
}
}
}// end of doSweep
/*
* inverseMatrix
* 目的 : 引数で与えた行列について
* Gauss-Jordan Elimination を用いて逆行列を求める。
* 引数 : a[][] 係数行列。
* : x[][] a の逆行列を格納する。
* 戻り値 : boolean a が正則なら真
*/
static boolean inverseMatrix(double a[][],double x[][]){
// ここから 目的のコードを加えましょう。
// (D)
// ここまで
}// end of inverseMatrix
}// end of class Sample_inverseMatrix解説
以下にコードを加えた部分のメソッドを示します。コードを実行、
ガウス-ジョルダン法の計算手順では、
/*
* regulatePivot
* 目的 : 係数行列のピボット値が適正になるように調整する。
* 具体的には、現在注目しているピボットのある列について、
* 最も大きな数値のある行と、現在のピボット行を交換する。
* 引数 : a[][] 係数行列。
* : b[][] 定数配列。
* : k 現在注目しているピボット位置
*/
static void regulatePivot(double a[][],double b[][] ,int k){
double max = Math.abs( a[k][k] );
double temp = 0;
int rowOfMaxPivot = k;//最大のピボット候補値の格納された行の値
if(k != (a.length - 1)){//最終行でなければ続きを実行
for (int row = k+1; row < a.length; ++row){
//ピボット行の次の行から
if( Math.abs(a[row][k]) > max ){//より大きな値を見つけて
max = Math.abs(a[row][k]);//最大値として保管し
rowOfMaxPivot = row;//その行が何行目か保管しておく。
}
}
}
if(rowOfMaxPivot != k){
//最大値のある行が、現在注目しているピボットのある行でなければ
//最大値のある行と、現在のピボット行とで値の交換
//現在のピボットのある列を含めて右側の値について交換を実施。
for (int col = k; col < a[0].length; ++col){
temp = a[k][col];
a[k][col] = a[rowOfMaxPivot][col];
a[rowOfMaxPivot][col] = temp;
}
for( int col = 0 ; col < b[0].length; ++col){
temp = b[k][col];
b[k][col] = b[rowOfMaxPivot][col];
b[rowOfMaxPivot][col] = temp;
}
}
}// end of regulatePivot
/*
* doSweep
* 目的 :掃き出し処理。
* 引数 : a[][] 係数行列。
* : b[][] 定数配列。
* : k ピボット位置
*/
static void doSweep(double a[][],double b[][],int k){
double pivotVal = a[k][k]; //掃き出し前のピボット値を保持
double pivotColVal = 0; //これから掃き出しを行う行のピ
//ボット列の値を保持しておく。
//ピボット値のある行の各要素を、ピボット値で割る。
for( int col=k; col < a[0].length; ++col)
a[k][col] = a[k][col] / pivotVal;
for( int col=0; col < b[0].length; ++col)
b[k][col] = b[k][col] / pivotVal;
//全ての行で、ピボット位置以外のピボット列の値をゼロにする。
//その副作用として、ピボット列以外の要素同士も減算を行う。
for( int row = 0; row < a.length; ++row){
pivotColVal = a[row][k];
if( row != k ){
for( int col = k; col < a[0].length; ++col)
a[row][col] = a[row][col] - pivotColVal * a[k][col];
for( int col = 0; col < b[0].length; ++col)
b[row][col] = b[row][col] - pivotColVal * b[k][col];
}
}
}// end of doSweep
/*
* inverseMatrix
* 目的 : 引数で与えた行列について
* Gauss-Jordan Elimination を用いて逆行列を求める。
* 引数 : a[][] 係数行列。
* : x[][] a の逆行列を格納する。
* 戻り値 : boolean a が正則なら真
*/
static boolean inverseMatrix(double a[][],double x[][]){
//引数で与えられた変数の次元は適切か
if ( isSquareMatrixDouble(a) &&
isSquareMatrixDouble(x) ) {
//引数に与えた変数に問題なし。
//x に単位行列をセット
for(int row = 0; row < x.length; ++row){
for(int col = 0; col < x[0].length; ++col){
if(row == col) {
x[row][col] = 1;
} else {
x[row][col] = 0;
}
}
}
for (int k=0; k < a.length; ++k){
//k は現在注目しているピボット位置
regulatePivot(a,x,k); //ピボットの調整
if (a[k][k] == 0){
//ピボットがゼロのとき、正則ではない。異常終了
return false;
} else {
//ピボットの値が正常なので掃き出し実行。
doSweep(a,x,k);
}
}// of for k
//ここまで来たと言うことは、正しく計算が終了しているということ。
} else {
//引数に与えた変数に問題がある。
return false;
}
//ここまで到達したということは成功
return true;
}// end of inverseMatrix行列の数学の最後に
長きにわたった行列の数学ですが、
連載の中で学習したアルゴリズムを頻繁に利用することが考えられる方は、
科学技術計算におけるJava言語の地位はまだまだ確立されたものとは言えません。目的に合わせた活用のための仕事の余地が多く残されています。参考書やオープンにされているソースコードを研究して、



