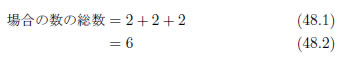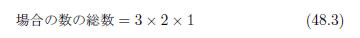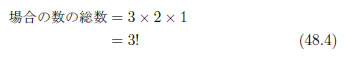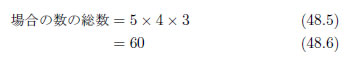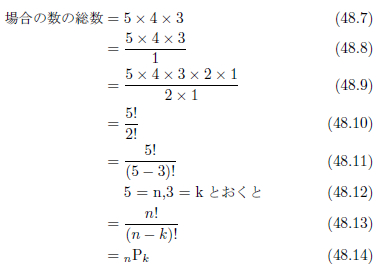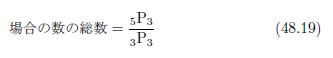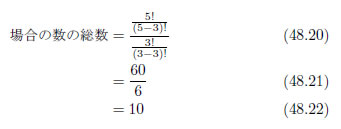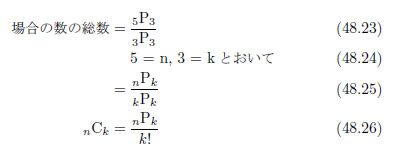柔道の技は、全て単発で決まるものはありません。国際試合ではヨーロッパJudoの影響で、飛び込んで足を取る技が多く見られますが、伝統的な講道館柔道では「品のない行為」と見なされます。小さい頃から伝統的な日本柔道を稽古してきた柔道家は、先ずしっかりと襟と袖をつかみ、相手の体勢を崩して技を決めようとします。1つの技を決めるために、いくつかの技術を組合せ、相手の想像もつかない動きを工夫するのです。背負い投げひとつを取ってみても、組んですぐに入る場合、大内刈り、小内刈り、出足払いなどをかけてみる、相手がこらえる、あるいはかわす、こちらが更に押し込む、相手は前方向へこらえる、チャンス、背負い投げ！自分の得意技が決まるかどうかは、技に至るまでの小技の順番や組合せにかかっています。いかに相手の予想を裏切るか。どの格闘技もそうでしょうが、頭を使わなければ勝てません。

今回学ぶのは、確率の数学に不可欠な、順列と組合せの数学です。プログラマの素養の1つとして、今回ご紹介する内容は確実に身につけておきましょう。小技として、大技として、きっと意外なところで、そして思うよりも多く助けられることがあるでしょう。

確率と順列・組合せ

確率の値を求めるためには、それ以上分割できないほどに粒分けされた事象、根本事象[1]の総数、すなわち全事象の数が必要です。根本事象は全て「同様に確からしい」ことが条件です。そして、確率を求めたい事象の数も必要です。全事象の数や確率を求めたい事象の数を求めるには、簡単な問題ならば一つ一つ書き出して数え上げるのが一番確実で間違いありません。

しかし、いちいち数え上げていては追いつかないような問題もあります。例えば、「⁠トランプから取り出した任意の二枚の組合せの数を答えてください」なんて言われたら、どうします？もちろん、全ての場合を書き出して、数え上げても結構ですが、そのためには大変な時間が掛かることでしょう。上手に、効率よく計算する方法があるならば、是非とも知っておきたいですね。それが順列・組合せの数学です。

今回は、順列と組合せの数学を簡単におさらいしましょう。闇雲に公式を当てはめて問題を解くのではなく、式の意味を理解して使えるようにすることが目標です。

順列

順列[2]とは、異なるn個のものの中から順番にk個ほど取り出す場合の数のことです。

例えば、赤、白、黄色の玉を順番に並べる場合の数はいくつあるでしょうか。これを3つから3つを選ぶ順列といいます。樹形図[3]を作ってみましょう。

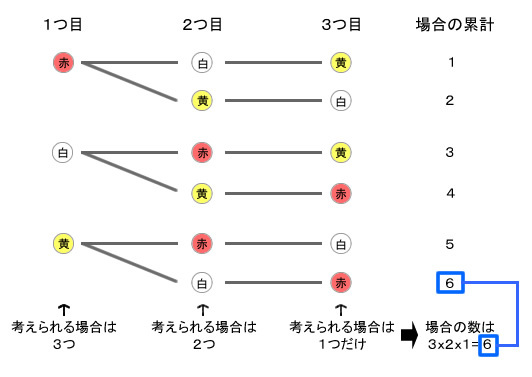
1つ目の玉は3つの中から選び取りますから、場合の数は3です。2つめの玉は、残った2つの中から選び取りますから、場合の数は2です。3つ目の玉は、残った1だけ。こうして順番に考えていくと、できあがった樹形図から場合の数の総数は、樹形図の葉の数（右端の場合の数）に注目すると、次のように計算できます。

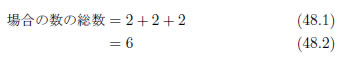
となります。式48.1は、次のように書くことも出来ます。

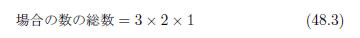
よく見ると、この計算は記号で置き換えられそうですよ。

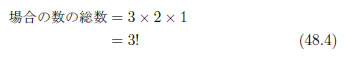
階乗の記号で置き換えられましたね。公式など一切使わず、問題の意味だけから結果を得ることが出来ました。

もう一つ考えてみましょう。5つの玉から3つ選ぶ順列はどうなるでしょう。樹形図を作って調べてみましょう。ただし、今回は数が多くなりますので、一部分のみを書いて全体は省略します。

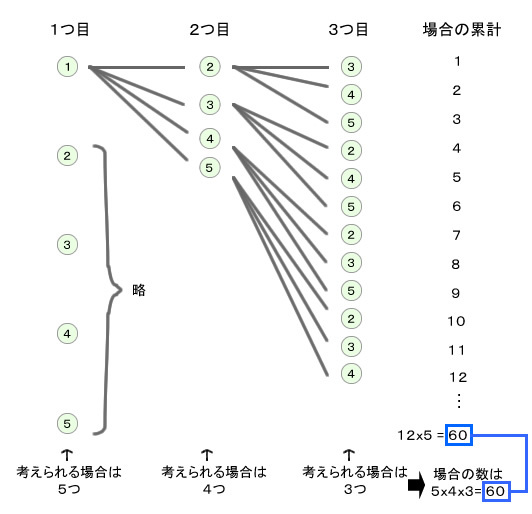
樹形図から、1つ1つ場合を数え上げても60、1つ目の場合の数・2つ目の場合の数・3つめの場合の数と計算しても同じく60であることがわかりますね。

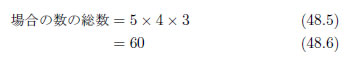
式48.5は特に公式を使ったわけではなく、意味を考えれば自然と求められる式でしたね。順列といえば_nP_kを思い浮かべますが、あれ？どんな公式だったっけ？と困ってしまう人が少なくないはずです。順列の意味を考えれば、公式は必要がない、というと極論ですが、今回の例のような簡単な場合から公式を導くと良いでしょう。

式48.5から次のように式を変形して公式を導いてみましょう。

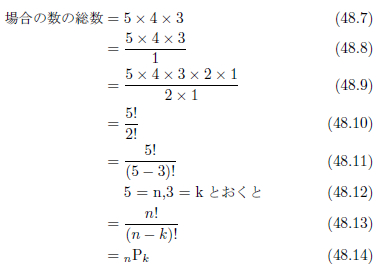
こうして教科書で習ったような順列の式が得られましたね。公式の記憶が苦手ならば、意味を記憶しておくと良いでしょう。意味のない記号を覚えるのはどなたも苦手なものですが、意味のあるものは記憶に残りやすいものです。

組合せ

組合せ[4]とは、異なるn個のものの中からk個を取り出した場合の数のことです。取り出す順番、並べる順番は問いません。先ほど同様、3つの玉を用いて、3つの玉の中から3つを取り出す組合せを調べてみましょう。

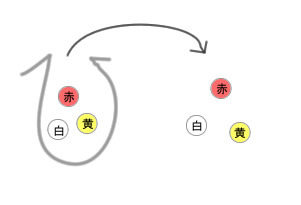
おや、そのような場合は1つしかありませんね。組合せの数は順列よりは少ないですね。

図48.2を見ると、3つの玉から3つを取り出す順列は6通りありました。しかし、順番を考えなければ、これらは全て同じ場合、すなわち重複する組合せです。同じ場合が6通りありますから、次の式のように考えることが出来ます。

さて、もうひとつ別の場合を考えてみましょう。5つの玉から3つ選ぶ組合せはどうなるでしょう。

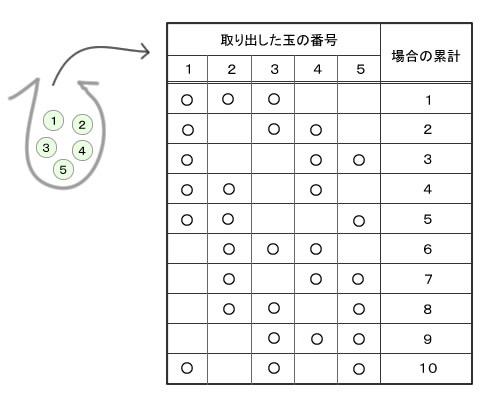
この図のように、考えられる組合せを全て列挙しても良いのですが、組合せの数が欲しいだけならば理論的に求めたいものです。何より玉の数が多くなれば列挙するのは現実的ではありません。次に組合せの数を理論的に求めてみましょう。5つの玉から3つ選ぶ順列から、同じ組合せを除外すれば良いのです。3つの玉の順列は、先ほど求めたとおり6通りです。これで筋道がつかめました。

5つの玉から3つ選ぶ組合せは、5つの玉から3つ選ぶ順列の数を、3つの玉の順列の数で割ってやれば良いことがわかりました。

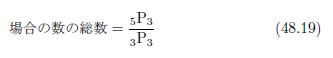
₃P₃を計算するためには0!=1が必要ですね。

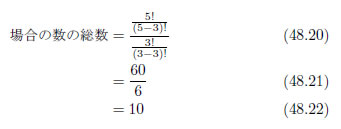
以上の式操作の結果、場合の数の総数は10であることがわかりました。1つ1つの場合を数え上げ、重複する場合を消去していくのが一番確実なのですが、60通りもある順列の中の重複をチェックするのは、いやですよね。式で求められれば、こんなにありがたいことはありません。さて、教科書で見るような_nC_kの公式はどうすれば得られるでしょうか。

式48.19を次のように操作します。

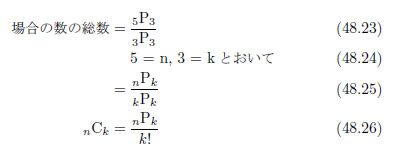
式48.26は教科書で見ることが出来る順列と組合せの関係式ですね。これを記憶しておけば、組合せの公式を覚えておく必要はないでしょう。

今回はここまで

今回は、順列と組合せの最も基本的な考え方と、P記号・C記号の意味と式を紹介しました。

多くの場合、専門分野ごとに公式集という書籍があり、公式集を見ればわざわざ導かなくとも正しい式を知ることができます。専門家にとって、そのような書籍と、その式が載っているということを知っていることが大事です。仕事に当たっていちいち式を導くなんてやっていられないからです。しかし、いざ仕事に変化が生じた場合、公式では対応ができない状況が起きます。公式を場合にあわせて変形しなければならないのです。そうしたとき、公式が導かれた意味・経緯を知らなければ対応できません。

プログラマは、あらゆる分野に精通しているわけではありませんが、あらゆる分野のソフトウエアを作ることを要求されます。そんなときに、今回紹介したような、式の導出操作が役に立ちます。式の背景にある情報こそ、正しく目的通りに動作するソフトウエア作りに必要だからです。手数がかかっても、式の導出・変形のチャンスあるごとに丁寧にこなしておくようにしましょう。