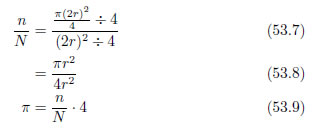柔道の背負い投げは、文字通り背負って投げることもあります。では、自分の力では持ち上げられないような重い相手には使えないのでしょうか。実は、背負い投げは、相手を背負う必要が無い技なのです。ぴったりと相手の正面に自分の背を付けるように技に入りますからこの名前が付いていますが、実際に力を働かせる場所は取り(技をかける側)の腰、おしりの少し上ぐらいです。受け(技をかけられる側)に力の働く場所は重心の少し下、へそと股ぐらの中間か、それより下の部分です。コツは受けの重心を前へ引き出すこと。そして、受けの重心の下へ自分の体を入れれば、ちょうど石に躓いてこけるような形になり、受けはくるりと回転します。うまくいけば重さをほとんど感じません。
この背負い投げのコツを、1つの公式的に教えることはできません。受けと取りの体格差によって千差万別、立つ位置も変化します。多くのコンピュータ・ゲームのように、このアイテムでこの操作をすれば、この技が決まる、といった固定したものではないのです。
今回は、コインやさいころのときのような確率の分布と異なり、連続的で、無限の場合が考えられる事象を取り扱います。より一般的な事柄が取り扱えるように世界を広げるのです。では、始めましょう。
図54.1 同じ技でも千差万別

連続事象
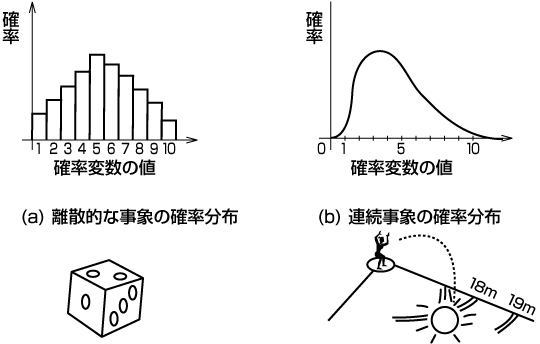
コインやさいころのように、裏か表、1、2、3、4、5、6と、かちっと場合分けできる場合を、離散的な事象[1]といいます。しかし、ボールを投げるとどこに落ちるか、といった試行の結果は、かちっと場合分けできません。巻き尺の目盛りは1mm単位で書かれているとしても、物の寸法は目盛りぴったりにはなりません。この、整数に対する実数の違いのような連続的な確率分布をもつ事象を連続事象[2]といいます。離散的な事象の確率分布は短冊を並べたようなグラフになり、連続事象の確率分布は連続な曲線(または直線)となります。
図54.2 連続事象とは
一様分布
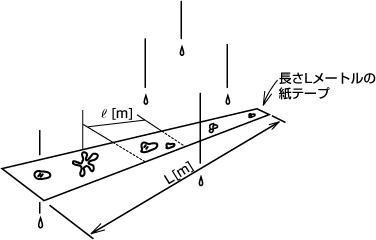
最も簡単な連続事象の確率分布の例として、一様分布を取りあげます。一様分布[3]とは、ある区間すべてに渡って確率が等しい確率分布のことです。例えば、長さ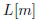 の紙テープを屋外に水平一直線に渡します。雨が降ってきたとき、テープ上のどこに雨粒が落ちるかは「同様に確からしい」と言えます。いま、テープのある区間
の紙テープを屋外に水平一直線に渡します。雨が降ってきたとき、テープ上のどこに雨粒が落ちるかは「同様に確からしい」と言えます。いま、テープのある区間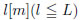 に雨粒が落ちる個数は、
に雨粒が落ちる個数は、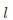 の長さに比例します。このとき、「雨粒の分布は一様分布である」といいます。長さ
の長さに比例します。このとき、「雨粒の分布は一様分布である」といいます。長さ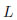 のテープに落ちる雨粒のうち、
のテープに落ちる雨粒のうち、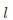 の区間に落ちる雨粒の確率
の区間に落ちる雨粒の確率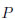 は次の式で表されます。
は次の式で表されます。
 図54.3 一様分布の例
図54.3 一様分布の例
モンテカルロ法
一様分布の連続事象をうまく利用した例にモンテカルロ法で円周率の値を求める方法があります。モンテカルロ法[4]とは、乱数を用いて数値シミュレーションをする方法のことです。
正方形にぴったり内接する円をとります。この図形を屋外において、雨が降るのを待ちます。ぱらぱらと降り始めた雨粒は、図形のどこにも均等に落ちることでしょう。図形の中に落ちた雨粒の数を数えることができれば、次のようにして円周率を計算することができます。
円の中に落ちた雨粒の数と正方形の中に落ちた雨粒の全ての数の比は、円の面積と正方形の面積の比と等しいはずです。雨粒の数の比は、正方形の中に落ちる雨粒のうちで円の中に雨粒の落ちる確率である、と言い換えることができます。こうして、確率と面積の等式を作ることができるのです。
図54.4 モンテカルロ法で円周率を求める
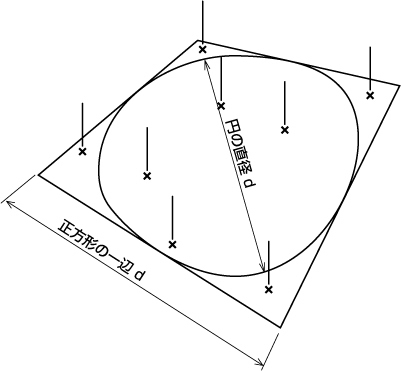
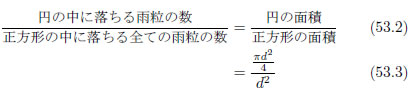
ただし、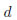 は正方形の一辺の長さであると同時に、内接する円の直径のことです。
は正方形の一辺の長さであると同時に、内接する円の直径のことです。
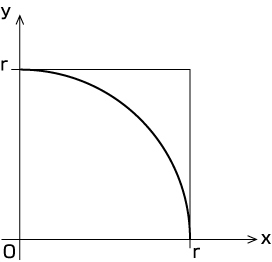
ここで、全ての雨粒の数を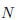 、円の中に落ちた雨粒の数をnとし、式53.3を円周率を求める式に変形・整理します。
、円の中に落ちた雨粒の数をnとし、式53.3を円周率を求める式に変形・整理します。

なんともシンプルな形となりました。式53.6を用いれば、魔法のように円周率が計算できるのです。実際には魔法でも何でもなく、数学に基づいてきちんと導かれた式ですから、安心して使うことができます。さあ、では雨が降るのを待ちましょうか・・・。と、そんなことはしていられませんね。私たちの手元にある便利な道具、コンピュータを用いてシミュレーションをしましょう。コンピュータ内の仮想の正方形の上に乱数の雨を降らせ、円の中に落ちた雨粒の数をカウントするプログラムを作って円周率を求めるのです。
問題 モンテカルロ法で円周率を求めましょう。
大変シンプルな問題ですから、ノーヒントで取り組んでみましょう。乱数の発生にはMathクラスを用いても結構ですし、せっかく作ったのですからDiceクラスを用いるのもよいでしょう。試行の回数は1000000回(百万回)としましょう。計算結果を標準出力に表示させてください。
解説
問題 モンテカルロ法で円周率を求めましょう
コードを簡単にするために、次の図53.5のように問題を読み替えました。
図54.5 4分の1円でモンテカルロ法
このように問題を読みかえても、結局最後の計算式は同じです。
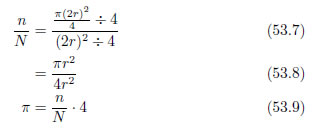 ソースコード:Sample_MC.java
ソースコード:Sample_MC.java
/*
問題 モンテカルロ法で円周率を求めましょう。
filename : Sample_MC.java
uses : Dice.class
*/
class Sample_MC {
public static void main(String[] args) {
int trial = 1000000; //試行回数
//Dice クラスを使った場合
int r = 1000; //円の半径
Dice dx = new Dice(r); //x 軸用ダイス
Dice dy = new Dice(r); //y 軸用ダイス
int hit = 0; //円の中の雨粒
double MC_Pi = 0.0; //円周率値
//Math.random を使った場合
int hit2 = 0; //円の中の雨粒
double MC_Pi2 = 0.0; //円周率値
//---------------------------------
System.out.println("モンテカルロ法"
+trial+"個雨粒を落とす。");
for (int i=0; i<trial; ++i){
if ( Math.pow(dx.roll(1),2)
+ Math.pow(dy.roll(1),2)
<= Math.pow(r,2) ) ++hit;
if ( Math.pow(Math.random(),2)
+ Math.pow(Math.random(),2)
<= 1 ) ++hit2;
if ( i % (trial/10) == 0 )
System.out.print("*");
}
System.out.println();
MC_Pi = (double) hit / trial * 4;
MC_Pi2 = (double) hit2 / trial * 4;
System.out.println("<試行結果>");
System.out.println("Dice クラス使用π="+MC_Pi);
System.out.println("Math クラス使用π="+MC_Pi2);
}// end of main
}// end of class Sample_MC
サンプルコードの実行結果を示します。
C:\>java Sample_MC
モンテカルロ法1000000 個雨粒を落とす。
**********
<試行結果>
Dice クラス使用π = 3.134884
Math クラス使用π = 3.140752
Mathクラスを使った方が若干精度が良いのは、Diceクラスでは乱数を整数で発生させているためでしょう。Mathクラスの乱数はDouble型ですので、Diceクラスよりは多様な値が得られます。しかし、どちらにしてもシミュレーション結果の精度は有効数字3桁程度です。精度がこの程度しか得られないのは、コンピュータで発生した乱数のばらつきが、思ったほど一様ではないことの表れです。理論的には、完全な乱数を用いていれば、より高い精度で円周率が得られるはずです。
今回はここまで
今回は、連続事象を紹介し、一様分布の連続事象の実例・応用例としてモンテカルロ法を用いた円周率計算を取りあげました。問題に取り組む中で、Java言語の乱数ユーティリティの性能がそれほど高くないことを図らずも実感したことでしょう。


![]() の紙テープを屋外に水平一直線に渡します。雨が降ってきたとき、
の紙テープを屋外に水平一直線に渡します。雨が降ってきたとき、![]() に雨粒が落ちる個数は、
に雨粒が落ちる個数は、![]() の長さに比例します。このとき、
の長さに比例します。このとき、![]() のテープに落ちる雨粒のうち、
のテープに落ちる雨粒のうち、![]() の区間に落ちる雨粒の確率
の区間に落ちる雨粒の確率![]() は次の式で表されます。
は次の式で表されます。


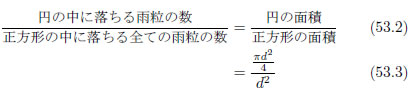
![]() は正方形の一辺の長さであると同時に、
は正方形の一辺の長さであると同時に、![]() 、
、