初めて戦う相手というのは、やりにくいものです。どこから手を付けたものか、判断の基準がありません。そんなときは、自分の得意な形と、考えられる限り最も一般的な手で始めてみるものです。必ずしもそれが当てはまるとは限りませんが、当てはまらなければ、どう当てはまらなかったかを観察し、戦略を切り替えて行けばよいのです。
今回学習する正規分布はそのような道具です。必ずしも全ての場合に当てはまる確率分布ではありませんが、山形の確率分布になる事象について一般的によく用いられるものです。これまでに学習した項目が総合的に用いられます。忘れてしまったところがあれば前に戻って復習しながら学習を進めてください。
図55.1 じっくり相手の出方を見よう

正規分布
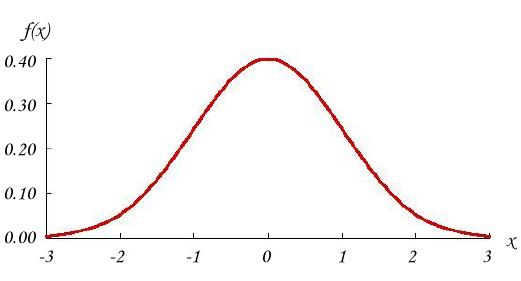
正規分布[1]とは、図55.2のような形の確率分布で、確率密度関数は式54.1で定義されます。式中のmは期待値、σは標準偏差です。確率変数Xの値xは実数です。
図55.2 正規分布
正規分布の確率密度関数を簡単に取り扱うために、確率変数の値xを次のように変換します。

式54.2の操作を標準化といいます。
標準化した正規分布の確率密度関数は次のようにシンプルになります。
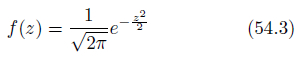
標準化の操作により、f(z)のzの平均値は0、標準偏差は1となります。確率密度関数が式54.3のようになる分布を、標準正規分布[2]といいます。
確率変数の値xをzに変換すると、教科書の巻末などによく掲載されている「正規分布表」が利用できます。正規分布表を利用できれば、式54.3を積分する手間を省いて必要な値を得ることが出来ます。これは大きなメリットです。
ところで、式54.1や54.3は指数部が複雑で、活字が小さいときや筆記した場合には読み誤り・書き誤りを生じやすくなります。そこで、指数関数の中でも底がe(ネイピア数)の場合には、式54.4のように書き改める流儀があります。便利ですので記憶しておくとよいでしょう。
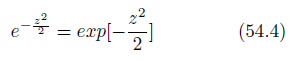
expは指数関数[3]の略記号です。
そもそも、正規分布はガウス[4]が山の高さを測定していたときに、発生した誤差の分布から発見し、それ以来誤差の分布を取り扱う時に用いられています。そのためガウス分布[5]とも呼ばれます。
正規分布を使う意味
2項分布の近似として
コインやさいころについての各種事象は、扱うコインやさいころの数や試行回数が少なければ、これまで学習してきた2項分布を用いて各場合の確率(確率密度関数の値)を導出できます。しかし、数が多くなると計算の手間が大きく、コンピュータを用いたとしても正確な値を求めるのが困難になります。100回を越えるような多数回の試行の2項分布の確率密度関数を近似したものが、正規分布の確率密度関数です。
nが100の2項分布の式なんて、考えたくもないでしょう。正規分布の確率密度関数なら、nの値が100でも1000でも計算は一瞬で済んでしまいます。ですから、工業製品の寸法値のばらつき評価や、テレビの視聴率の調査など、調査対象が多数の場合に正規分布が役立つのです。
統計的データの判定基準として
正規分布は多くの場合、あるデータについて、分布の中心に近いデータなのか、それとも中心から外れたデータなのかを読み取る、という使われ方をします。例えば次のような場合です。
- 「1000人の受験者の100点満点の試験で、ある受験生が70点を取りました。100人が合格するとして、この受験生には合格の可能性があるでしょうか。」
大雑把に言えばこの文章のような場合に正規分布が活用されます。データの集合は、グラフにすると正規分布のような形になると「仮定」して「推測」するのです。教科書などに掲載されている正規分布表は、確率密度関数の値ではなく、分布の中心(グラフの山のてっぺんのあるところ)から目的の位置までの積分値の表になっています。この数値がわかれば、目的のデータの位置が全体の何%なのかがわかるからです。
その他の確率分布
正規分布は多くの場合において有効な確率分布ですが、オールマイティではありません。正規分布はデータの数が大きい時によく当てはまりますが、データの数が小さいときや、特定の傾向を持ったデータの場合には他の分布を使用すべきであることを覚えておきましょう。
降り注ぐ雨の落ちる位置など均等な確率を取り扱う「一様分布」。複数個のコインやさいころを転がした場合の出目の確率を取り扱う「2項分布」。
発生率が極めて少ない事象の確率によく当てはまる「ポアソン分布」。宝くじの当選確率には「幾何分布」。銀行の待ち行列の時間間隔や原子の崩壊時間間隔を取り扱う「指数分布」。正規分布は数ある分布関数の中の1つにすぎません。確率分布といえば正規分布、という当てはめは、必ずしも成り立たないということを、記憶にとどめておきましょう。
しかし、どんな確率分布を示すとしても、その分布からとった確率変数の和は、和をとる数が多ければ、ほぼ正規分布に従います。これを中心極限定理[6]といいます。正規分布の重要性は、このことからもわかります。
問題 標準正規分布のz=0の点から任意のzまでの積分値を返すプログラムを作りましょう。
教科書の巻末等に掲載されている正規分布の数表は、次の式54.5の、標準正規分布の確率密度関数の積分について、aを0から4程度まで、0.01刻みで変えて積分値を求めたものです。

今回の演習では、z=0から1の積分値をJava言語のプログラムで近似計算して求めてみましょう。0.3413が得られれば正しく計算できたことにします。図55.3に大まかなヒントを示します。
図55.3 標準正規分布の確率密度関数を数値積分する
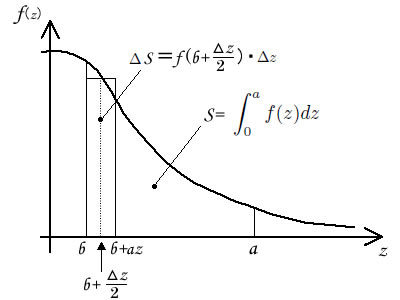
標準正規分布の確率密度関数は、スムーズな形状の曲線を描きますので、図のような方法で数表に掲載されている程度の精度を得ることができます。
積分といっても、関数のグラフと各軸で囲まれた部分の面積を求めるだけのことです。曲線を持つ図形ですから、簡単には面積が得られません。
そこで図形を細い短冊形に切り刻み、短冊の面積を合計します。図55.3のようにして積分値を求める方法を数値積分[7]といいます。
解説
問題 標準正規分布のz=0の点から任意のzまでの積分値を返すプログラムを作りましょう。
式をプログラムコードに置き換え、 ごとに短冊の面積を合計していくだけの単純な方法です。地道に組めばすんなりできあがるのですが、整数、実数の取り扱いを几帳面に行わないと変な誤差が発生します。解答例を示しますので、うまくいかなかった方は参考にしてご自分のコードを改善してください。
ごとに短冊の面積を合計していくだけの単純な方法です。地道に組めばすんなりできあがるのですが、整数、実数の取り扱いを几帳面に行わないと変な誤差が発生します。解答例を示しますので、うまくいかなかった方は参考にしてご自分のコードを改善してください。
ソースコード:Sample GetSND.java完成版
/*
問題 標準正規分布の積分を求めましょう。
filename : Sample_GetSND.java
*/
class Sample_GetSND {
public static void main(String[] args) {
int DIV = 10000; //標準偏差を何等分するか
double deltaZ = 1.0 / DIV; //微小長方形の幅
double S = 0; //積分結果
double z = 1; //面積を求めたいz 位置
double temp_z = 0;
//---------------------------------
System.out.println("標準正規分布を0 から"
+ z + "まで積分する。");
for (int i=0; i<(long)(z*DIV); ++i){
temp_z = (double) i / DIV + 0.5 * 1.0 / DIV;
S += 1.0 / Math.sqrt(2*Math.PI)
* Math.exp(- Math.pow( temp_z ,2 ) / 2)
* 1.0 / DIV;
}
int prec = (int) Math.log10(DIV);
System.out.println("<結果>結果の精度は小数点以下"
+ prec + "桁程度です。");
System.out.println(S);
}// end of main
}// end of class Sample_GetSND
実行結果は次のようになりました。
C:\>java Sample_GetSND
標準正規分布を0から1.0まで積分する。
<結果>結果の精度は小数点以下4桁程度です。
0.3413447461693643
今回はここまで
今回は標準正規分布の定義式を確認し、正規分布表に掲載された数値を近似的に計算する方法を学びました。


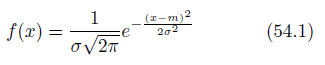

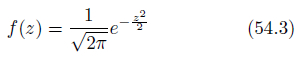
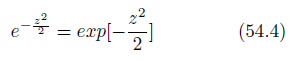


![]() ごとに短冊の面積を合計していくだけの単純な方法です。地道に組めばすんなりできあがるのですが、
ごとに短冊の面積を合計していくだけの単純な方法です。地道に組めばすんなりできあがるのですが、


