バスケットボールでは、
とかく細かな動きにとらわれると、

移動平均
移動平均
平均をとるというと、
移動平均は、
ノイズの多い信号データを受け取った場合に、
株価の細かな変動を平滑化して、
図58.
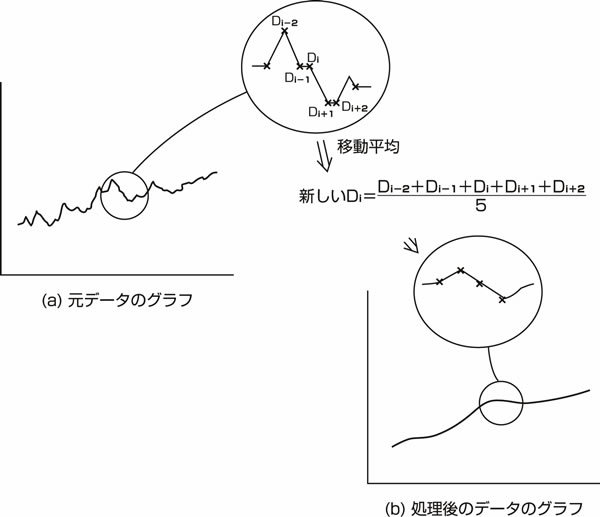
例えば時系列に並んだ100個のデータがあるとします。平均をとる範囲を5とすると、
![]()
先頭から順番にデータを処理する場合には、
問題 移動平均をとるプログラムを作りましょう
前回作成したデータファイルを読み込んで、
c:\java> java Sample_MovingAverage < st_sample002.csv > result_ma.csvこの操作により、
ソースコードの大枠を次に示しますので、
/*
* Sample_MovingAverage.java
* コンマで区切られた2つひと組の数値を
* 標準入力から読み込んで、ArrayListにため込み、
* 移動平均をとり、標準出力へ出力する。
* usage : c:\java> java Sample_MovingAverage result_ma.csv
*/
import java.util.*; // StringTokenizer
import java.io.*; // BufferedReader
public class Sample_MovingAverage {
public static void main(String args[]) {
//入力:カウント
ArrayList a = new ArrayList();
//入力:データ
ArrayList b = new ArrayList();
//出力:移動平均値
ArrayList c = new ArrayList();
int count = 0;
BufferedReader d = new BufferedReader
(new InputStreamReader(System.in));
try {
int tokens = 0;
do {
String str = d.readLine();
if (str == null) break;
StringTokenizer aSt = new StringTokenizer(str,",");
if (aSt.countTokens() != 2) {
System.out.print("Input Error\n");
System.exit(1);
}
tokens = aSt.countTokens();
++count;
a.add(Double.valueOf(aSt.nextToken()).doubleValue());
b.add(Double.valueOf(aSt.nextToken()).doubleValue());
} while (tokens ==2);
}
catch(IOException e) {
System.out.println("IO Error");
System.exit(1);
}
//データb の移動平均をとる。
CalcMovingAverage(b,c,5);
//移動平均の出力
int i = 0;
Iterator iterC = c.iterator();
while(iterC.hasNext()) {
System.out.println(i + "," + iterC.next());
++i;
}
}// end of main
/*
* 目的: 移動平均をとる
* 引数: data 元データのArrayListへの参照
* result 移動平均値のArrayListへの参照
* 移動平均の計算結果を格納する
* range range個の平均をとる
*/
static void CalcMovingAverage(ArrayList data,
ArrayList result,
int range) {
//ここからコードを補充してください
//ここまでコードを補充してください
}// end of CalcMovingAverage
}// end of class 解説
問題 移動平均をとるプログラムを作りましょう
コードの補充が完了した関数を示します。注目するデータ位置に対して前方範囲の平均を取るシンプルなアルゴリズムです。
/*
* 目的: 移動平均をとる
* 引数: data 元データのArrayListへの参照
* result 移動平均値のArrayListへの参照
* 移動平均の計算結果を格納する
* range range個の平均をとる
*/
static void CalcMovingAverage(ArrayList<Double> data,
ArrayList<Double> result,
int range) {
Double sum = 0.0;
Double ma = 0.0;
for (int i=0; i<range ; ++i) sum += data.get(i);
ma = sum/range;
for (int i=0; i<(range/2); ++i) result.add(0.0);
result.add(ma);
for (int i=range; i<data.size(); ++i){
sum = sum - data.get(i-range)+data.get(i);
ma = sum / range;
result.add(ma);
}
}// end of CalcMovingAverage引数rangeから導かれる、
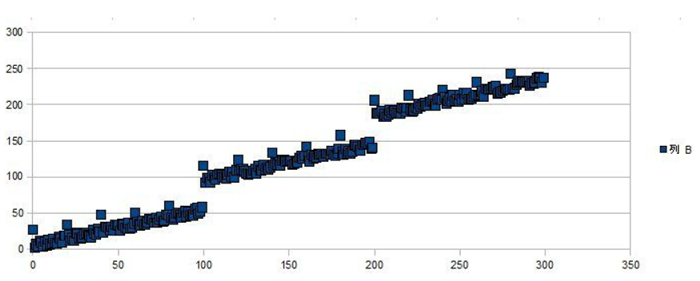
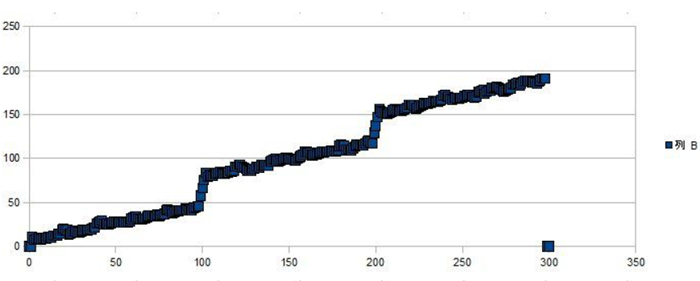
図58.
今回のサンプルデータは、
今回はここまで
移動平均という、
表計算ソフトウエアを利用しても良いのですが、



