どのスポーツにも「フェイント」があります。右と見せかけて左、前と見せて後ろ。フェイントをかけられる側としては、相手が何をしようとしているのか、それまでの相手の行動から、最後の一瞬までをしっかりと見届け、判断します。フェイントそのものは大きな動作であることが多いのですが、フェイントの後の行動は、それまでの行動とあまり大きく変えることは出来ないものです。「流れ」というものがあります。流れを感じることが出来れば大変有利です。
今回から始まる回帰直線は、まさにそのような利点のある統計的な数学手法です。
では、始めましょう。
図59.1 変化の中から次を読む

線形回帰
線形回帰(※1)とは、ばらつきを持ちながらもある傾向をもった統計データに対して、その傾向をy=ax+bといった一次式で表現することをいいます。また、線形回帰によって得られた直線のことを回帰直線[2]といいます。
図59.2に例を示します。
図59.2 WikiPediaに掲載された線形回帰のグラフ例
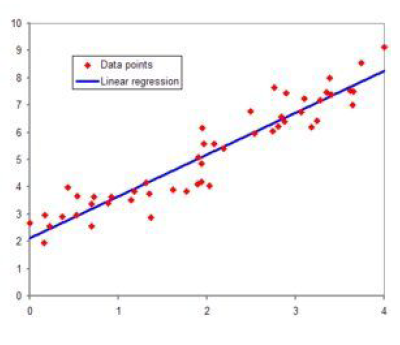
赤で示される点がデータで、無数に散らばるデータの傾向として、最も妥当と思われる線分を引いたのが青い直線です。この青い直線のことを回帰直線といい、どうやってこの回帰直線を引くか、というのが今回の内容です。
中学生や高校生の頃は、理科の実験の結果のグラフに、フリーハンドや物差しで、「だいたいこの辺!」と気合いで線を引いていたことと思います。
厳密にデータを分析したい場合には、そのような不安定な「気合い」に頼ることは出来ません。なるべく理論的にしっかりした線が欲しいところです。
Ofiiceソフトで回帰直線
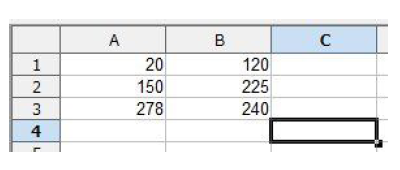
OpenOfficeのCalcを立ち上げましょう。そして、次の図59.3のようにデータを入力してください。
図59.3 テストデータをOpenOfficeのCalcに打ち込んだところ
第57回で紹介した手順を参考に、散布図を作成しましょう。その際、作成する散布図は、プロットしたデータを全て直線で接続する「点および線」を選択してください(図59.4)。
図59.4 作成する散布図は線付きのものにしましょう
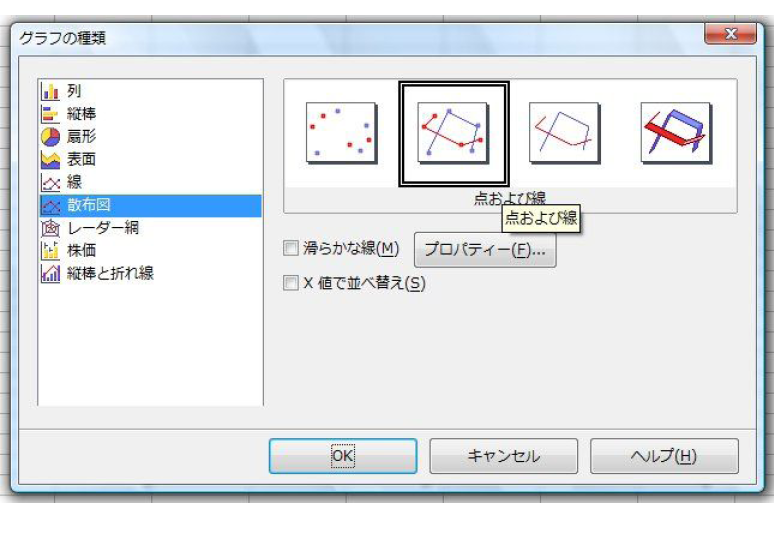
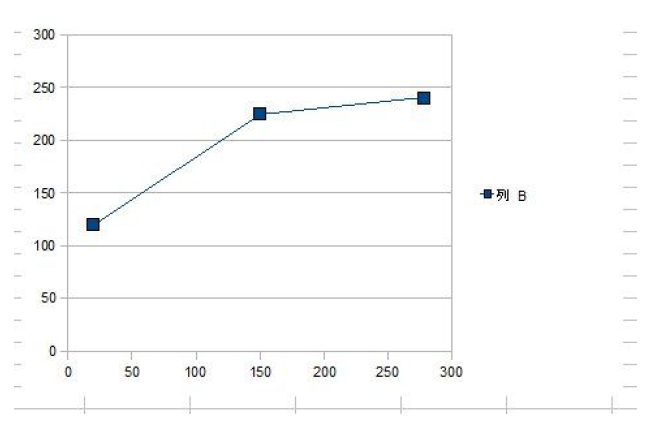
図59.5のようにグラフ用紙にデータをプロットすると、どうやらデータの傾向を表す直線を一本引くことが出来そうです。
図59.5 テストデータを用いてOpenOfficeのCalcで散布図を描いたところ
散布図のデータをつなぐ直線を右クリックすると、図59.6のようなポップアップメニューが表示されます。このメニューから「オブジェクトの属性」を選択してください。
図59.6 散布図のデータ曲線を右クリックしたところ
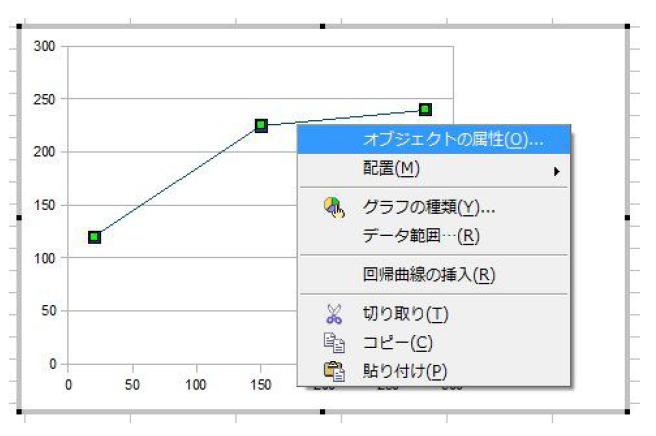
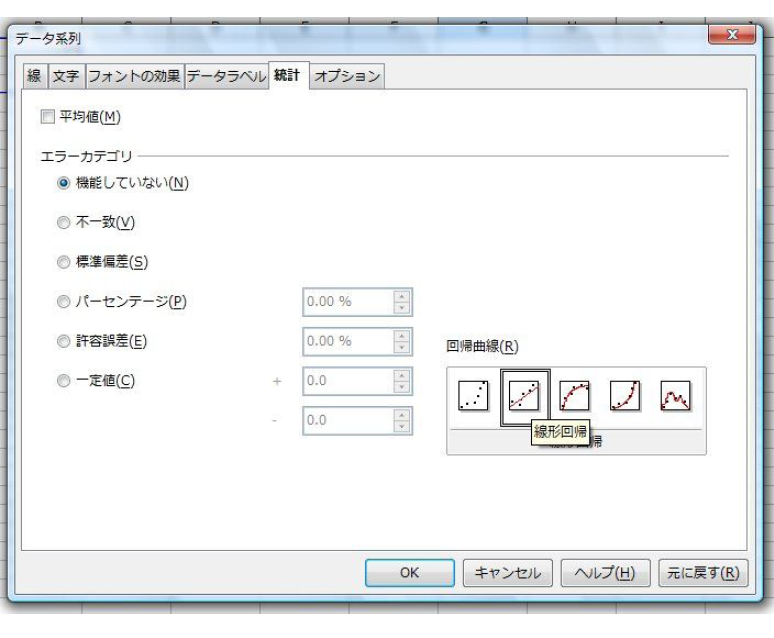
図58.7のダイアログが表示されますので、「統計」タブを選択し、右下の「線形回帰」をクリック、「OK」ボタンをクリックしてください。
図59.7 「オブジェクトの属性」を選択して表示されたダイアログ
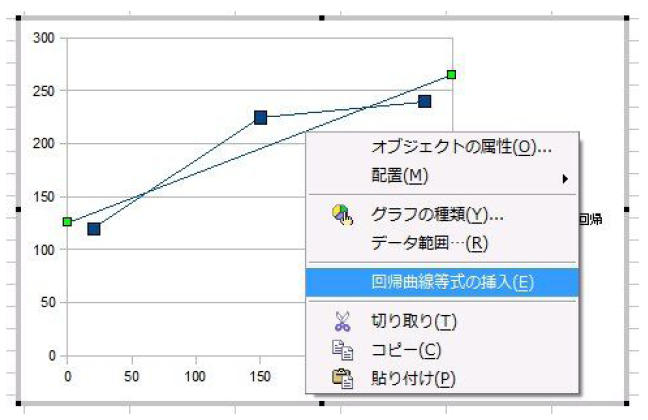
表示された回帰直線を右クリックすると、図58.8のポップアップメニューが表示されます。この中の「回帰曲線等式の挿入」を選択しましょう。
図59.8 回帰直線を右クリックし、ポップアップメニューから回帰曲線等式の挿入を選択
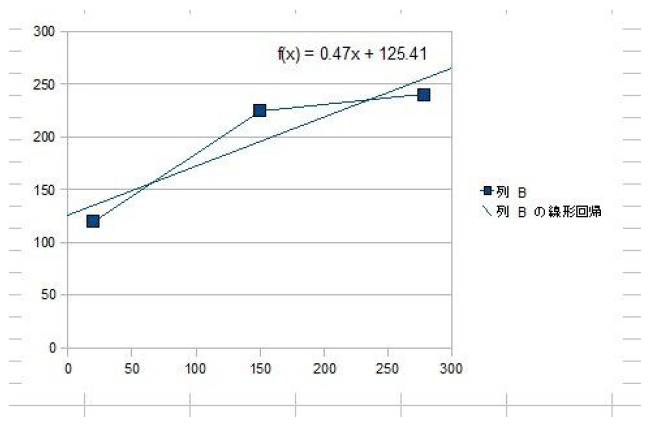
上記の手順で作成されたグラフが図58.9です。
図59.9 回帰直線の例 テストデータを用いてOpenOfficeのCalcで回帰直線を描いたところ
Officeソフトを使えば、以上のようにして手軽に回帰直線を得ることが出来ます。出力も美しいですから、ほとんどの場合はこれで事足りることでしょう。この程度のデータ数、また単にグラフが欲しいだけでしたら、自分でプログラムを作るまでもありません。
今回はここまで
今回は、ばらついてはいるが、ある直線的な傾向を示しているデータ群から、その傾向を示す一次等式、回帰直線をオフィスソフトを利用して手軽に得る方法を紹介しました。次回は、回帰直線を得る方法を詳しく学び、Java言語でグラフを描いてみましょう。












