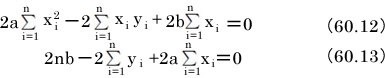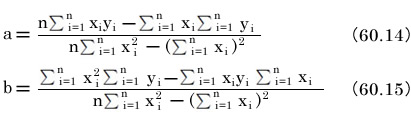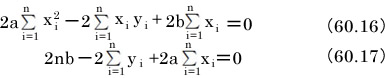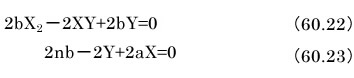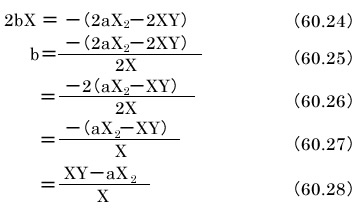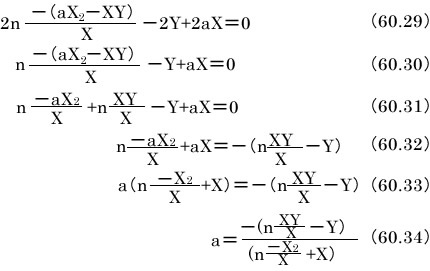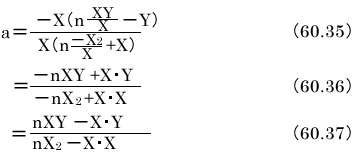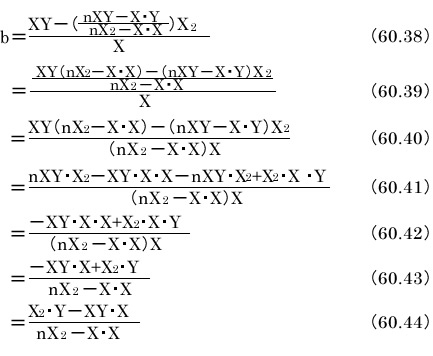今回は回帰直線を得るためのひとつの方法、最小二乗法をしっかりと紹介します。「コンピュータ数学」と銘打っていますから、遠慮なく数式を出します。高校数学から少しはみ出す部分がありますが、記号の奔流にだまされず、実はそんなに難しくないことに気付いていただけると幸いです。
最小二乗法とは
最小二乗法[1]とは、調査や測定によって得られた「ばらつき」のあるデータに対して、最もまんべんなく当てはまる直線や曲線の式を得るための数学的手段です。直線を当てはめる場合を特に線形最小二乗法[2]といいます。
得られた回帰直線の式を使えば、データのない区間について、値の予想ができます。データに誤差があると考えられる場合は、真の値を予想することが出来ます。なにより、バラバラだったデータの集合が、ひとつの一次式で表現できるというのは魅力的です。
最小二乗法は、工学に限らず広い分野で活用されています。プログラマは最小二乗法を「意味がわかって」活用できるようにしたいですね。
最小二乗法の原理
ある現象の測定結果m1(x1,y1),m2(x2,y2),m3(x3,y3)を得たとしましょう。これらのデータを得たあなたは、次の2つのうち、どちらかの要求を持っているとします。
- 現象の傾向を知るために、データに最も当てはまる直線の式を得たい
- 本来一直線上にデータが並ぶはずの現象であるため、本来とるべき値を示す直線の式を得たい
どちらにせよ、図60.1のように回帰直線の式y=ax+bを得たいのです。
図60.1 回帰直線と測定値の差
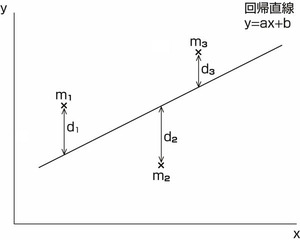
各測定値と予想した直線との差[3]d1,d2,d3の二乗の合計をSとします。
二乗の合計をとるのは、単純合計では直線との差が相殺されてしまうからです。それならば絶対値をとればよい、と思うのですが、手順を単純で機械的にするために、二乗する方が都合がよいのです。
回帰直線と測定値のy座標の差の二乗の合計Sは次の式になります。

最小二乗法は、このSを最も小さくするような直線y=ax+bの係数aとbを求める方法です。
n個のデータがある場合の回帰直線y=ax+bの定数a、bは以下の式で得ることができます。
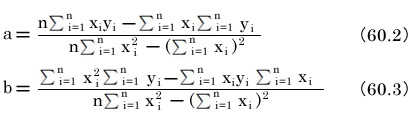
式60.2と60.3に測定値を次々代入し計算していけば、機械的に回帰直線の定数値aとbが得られます。これはコンピュータの得意とする作業です。
では、式60.2と60.3を導出しましょう。
数式の導出
途中、偏微分という方法を利用するので、高校生までの数学では理解できない!と早とちりしないで下さい。ここで利用する偏微分は高校数学で学習する微分とほとんど違いはないのですから。
回帰直線と測定値の差をとる
これから求めたい回帰直線y=ax+bと測定値mn(xi,yi)との差dは次のように書き表します。この式は、x座標値が等しいとき、測定値と回帰直線の式のy座標値にどれだけ差があるか、と読むことが出来ます(図60.1より)。

差の二乗の合計をとる
単純にdiの合計をとると、正の値と負の値が打ち消しあってしまいます。
ばらつきの多いデータでも、合計をとると小さな値にしかならないということが起こります。ばらつきの多いデータならば、合計の値が大きくなって欲しいのです。それで、diが正であろうが負であろうが、予測する直線とどれだけ離れているかを得るために、二乗してから合計するのです。
こういうわけで、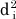 の合計であるSは次の式になります。
の合計であるSは次の式になります。
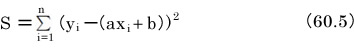
式の展開と整理
式60.5を展開し整理します。
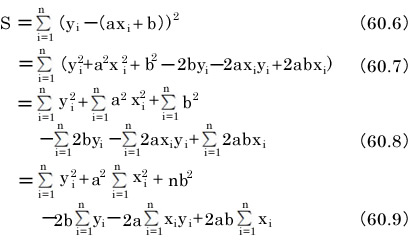
混乱しやすい事項の解説
式60.9から、定数aとbを求める方程式を導きます。
混乱しやすい事柄をここで確認しておきます。x、yが変数でa、bが定数であるという固定観念がありませんか?そのため、これから式をaやbについて微分する、というと抵抗感があるかもしれません。
現在学習している最小二乗法の式においては、xとyは測定値として与えられています。いわば定数です。未定の直線の式y=ax+bを決定するためにaとbを知りたいのですから、ここでは未知数・変数がaとbなのです。
aとbを変数として式を見る
Sをaとbの関数であると見ましょう。bを固定(bを定数と考える)すると、Sはaに関する二次関数です。図60.2に示すように、そのグラフは下に凸であると考えられます。グラフの下向き頂点がSが最小の位置です。
図60.2 下に凸のグラフとその接線
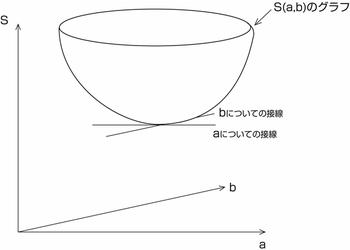
頂点を見つけるには、頂点に接する直線を求めます。グラフに接する直線は、曲線の式を微分することで求めることができます。
偏微分
二つの変数がある場合に、どちらかの変数を固定して、もう一方の変数で微分することを偏微分[4]するといいます。偏微分の記号は∂(「ラウンド」と読む)です。
微分して得られる式を導関数[5]と呼ぶのと同様、偏微分して得られる式を偏導関数[6]といいます。
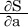 は、aについて微分公式をSにそのまま当てはめるだけです。高校で学習した微分の公式がそのまま使えます。変数bは定数値として扱います。
は、aについて微分公式をSにそのまま当てはめるだけです。高校で学習した微分の公式がそのまま使えます。変数bは定数値として扱います。
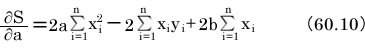
同様に、b について偏微分します。今度はaを定数値として扱います。
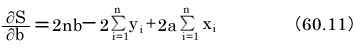
条件をあてはめて連立方程式をたてる
こうして得られた二つの式は、グラフの接線の傾きを表しています。たとえて言えば、すり鉢を正面と横から眺めたときの、最も低い位置を探しているのと同じです。傾きゼロの場合を見つけるわけですから、二つの式それぞれ、全体の値を0とします。こうして2つの等式が完成しました。これらをa、bについての連立方程式として解くのです。
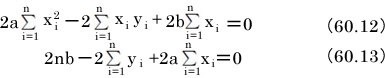
連立方程式を解く
式60.12と60.13を計算すると次の結果を得ることが出来ます。
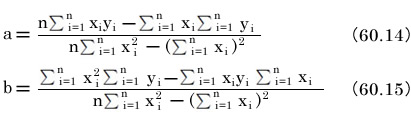
以上の手順でこの式を得ました。
問題 回帰直線の係数を求める連立方程式を解きましょう
式60.12と60.13からなる連立方程式を解き、解の式60.14と60.15を導いてください。
解説
問題 回帰直線の係数を求める連立方程式を解きましょう
以下に導出の手順を示します。長い式ですから、途中で書き漏らしを起こさないように慎重に操作しましょう。
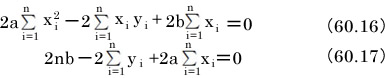
この連立方程式をそのまま操作してもよいのですが、出来るだけ楽をしたいので、次のように読みかえます。

この読みかえは、プログラマにとって日常的な操作です。合計計算の結果を変数に格納して用いるのと同じですね。
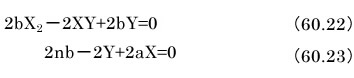
うそのようにシンプルになったと思いませんか?
では、この連立方程式からa,bの値を求める式を導きましょう。
式60.22をbイコールの形に変形します。
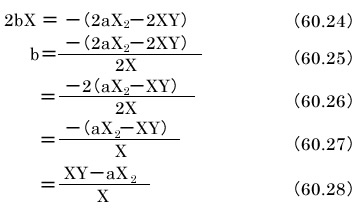
求めたbを式60.23に代入します。
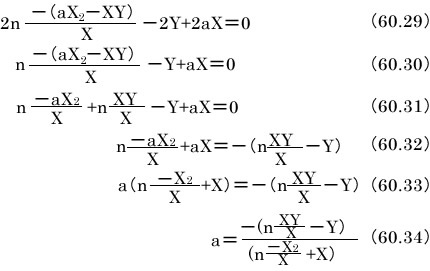
これで一応導けたのですが、当初目標とした形にまで整理しましょう。
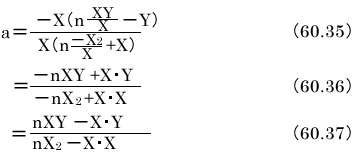
これを式60.28に代入します。
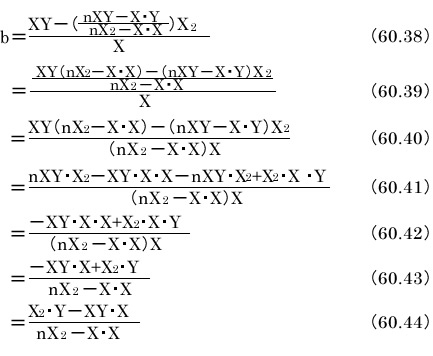
以上で目的の式が得られました。X,X2,Y,XYを元に戻せば式60.14と60.15が得られます。
今回はここまで
式の導出は無事にこなせましたか?地道に式を手で書いていくことが、理解の早道です。目でさっと流すだけでなく、鉛筆を手にとって紙に書き写してみましょう。その次は、式の意味を考えながら、自分の頭で式を導いてみてください。ここまですれば、何も難しいことはなかった、と感じられるはずです。

![]()
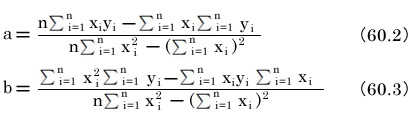
![]()
![]() の合計であるSは次の式になります。
の合計であるSは次の式になります。![]()
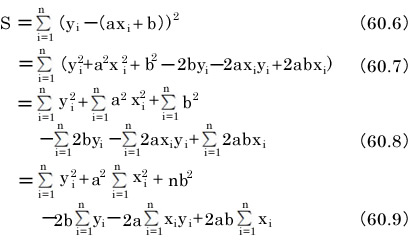

![]() は、
は、![]()
![]()