微分・積分というと、日常生活には全く縁がないもの、と思われがちではないでしょうか。しかし、「 速さ」「 加速」あるいは「減速」 、そして「移動距離」などと、歩いたり走ったり、自転車や自動車に乗っていれば、誰もが当たり前に使うこれらの言葉、考え方は、微分・積分と密接な関係があります。微分・積分は、私たちの日常生活に関わりが深い数学です。
しかし、例えば「エンジンの仕組みを知らなければ車に乗ることはできない」とか、「 電気信号の処理方法を知らなければ電話をかけられない」なんてことはありません。むしろ、そんなことを意識しないで使えるからよいのです。でも、この記事に関心を持ってくださったあなたは、きっと「もう一歩突っ込んでみたい」という気持ちがあるはずです。ただ便利に使うだけではもったいない、と思うからこそ、数学やプログラミングに関心がおありのはず。コンピュータの助けを借りて、微分・積分をより便利に使う方法を知りたくはありませんか?思うでしょう!微分・積分とプログラミングをミックスすると、「 こんな便利な道具を今まで使っていなかっただなんて」と思うはずです。では、はじめましょう。
図66.1 強力な助っ人、微分・積分 微分・積分とは
微分とは
微分 [1] とは次のように定義される関数です。
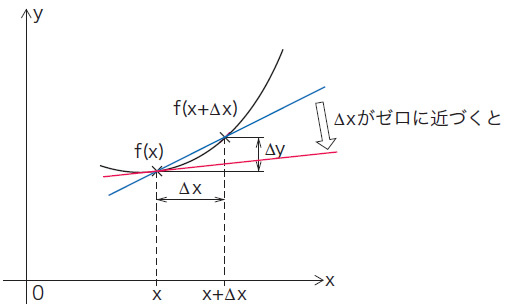
式66.2 によって、連続でなめらかな関数 f(x) の任意のxにおける微分係数 [2] が定義されています。元の関数 f(x) から導かれた、という意味を込めて、この関数を導関数 [3] と呼びます。導関数を求めることを、微分といいます。図66.2 に示すように、 ⊿x がゼロに近づくと、直線はxにおけるf(x)の接線に近づきます。導関数を求める、とは、関数の接線の式を求めることなのです。
図66.2 微分とは式66.2の左辺ライプニッツ流の記号です。高校の数学では次のようにも表示することを学習しました。
式66.3 の右辺をラグランジュ流の表記法といいます。長い式を書き下す場合に便利です。
積分とは
積分 [4] は、大きく2つに分けられます。1つは、座標平面上に関数が描くグラフと座標軸に囲まれた一定の部分の面積を求める方法で、これを定積分 [5] といいます。もう1つは、微分の逆の演算で、微分する前の関数を求める方法です。こちらを不定積分[6] 、あるいは「原始関数[7] を求める」といいます。
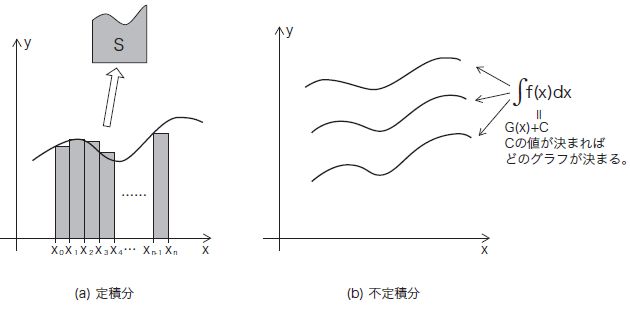
図66.3 積分とは(1)定積分
定積分について、もう少し具体的解説しましょう。例えば、図66.3 の(a)に示すように、ある曲線とx軸に囲まれた図形の面積Sを求めたいとします。どんなに複雑な形状の図形でも、細かくスライスすれば、長方形の短冊の集合に置き換えることができます。短冊の面積は「スライス幅×短冊の高さ」です。短冊の面積をすべて合計すれば、図形の面積とほぼ等しくなります。これが定積分の原理です。図形の形状を表す関数を f(x) 、図形をスライスする幅を ⊿x とすると、図形の面積は次の式で得られます。
このように、グラフ上のある部分の面積を、具体的な数値あるいは変数で示す方法が定積分です。
(2)不定積分
次に、不定積分について具体的な解説をします。
微分して f(x) になる関数を F(x) とします。このとき、次の式が成り立つとします。
このとき、 F(x) を f(x) の原始関数といいます。
定数項を含む式の微分をすると、定数項が消去されます。このことから、微分の逆演算である積分を行うと、定数項が表れるはずです。
この定数項 C を積分定数 [8] といいます。単純に積分しただけでは、この積分定数を決定できません。決定されない間は、積分定数を定数記号 C で表します。図66.3の(b)に示すように、 ∫ f(x)dx で求められるのは、関数の描く曲線です。曲線が座標平面のどこに位置するのかは定数Cによって決まります。
G(x)は微分の逆演算によって得られた関数で、原始関数と一致するのはCがゼロのときだけです。
不定積分では、積分の開始値、終了値を明記しない式66.7 のような書き方をします。このように、未決定な定数を含む原始関数を求める方法が不定積分です。
微分と積分の数値計算
微分や積分をコンピュータ・プログラムで計算することを、数値微分 [9] 、数値積分 [10] といいます。これらの数値計算に共通するありがたい性質は、あの大変な数に及ぶ微分・積分の変換公式を、基本的に使う必要がない、ということです。微分する前、あるいは積分する前の式があれば、あるいは連続したデータがあれば、微分値、積分値を近似的に求めることができるのです。これが微分と積分を数値計算することのメリットです。
数値微分
数値微分は、微分の定義に従い、次の式で計算を実行します。
コンピュータ・プログラムでこの計算を行う場合、 ⊿x の大きさは0に出来ないので、出来るだけ小さい値を用います[11] 。こうして、微分の公式を用いて導関数を求めることなく、微分係数の近似値を得ることが出来るのです。
数値積分
数値積分は、積分の定義に素朴に従い、関数のグラフと座標軸の間で囲まれた部分の面積を求める方法です。関数 f(x) とx軸で囲まれた閉区間[a,b]を、N等分して面積の合計値を計算します。
問題 微積分の基本的な問題を確認しましょう。
微分、積分の最も基本的で身近な活用シーンが「移動距離、速度、加速度」の3つでしょう。微積分を意識して使ってはいないのですが、これらの値の間には、それぞれ微積分という演算があります。微積分とコンピュータ数学の学習に入る前に、ウォーミングアップとして微積の定義・公式の復習をしておきましょう。
(a)微分を使って、速度、加速度の定義式を導きましょう。 (b)重力加速度の値から積分して、自由落下距離の式を導きましょう。
解説
問題 微積分の基本的な問題を確認しましょう。
(a)微分を使って、速度、加速度の定義式を導きましょう。
等速運動であれば、速度の定義式は次の通りです。
sは移動距離、tは移動時間です。
運動一般に適用するために、等速運動でない場合を考えなければなりません。その際、瞬間ごとの速度を定義すればよいのです。
以上で微分を用いた一般的な速度の定義式が得られました。
加速度は、速度の変化ですから、等加速度運動であれば次の通りです。
v0 は最初の速度、 v1 は時間 t が経過した後の速度です。 t は速度変化に要した時間です。これを一般的にするために、加速度が一定で無い場合を考えなければなりません。先ほど同様、瞬間ごとの速度の変化を定義すればよいのです。
以上で微分を用いた一般的な加速度の定義式が得られました。
こうして得られた式66.14,66.17 を見ると、速度や加速度を求めるために、必ずしも方程式が必要ないことがわかります。ある時点前後のデータがあれば、各値の近似値を計算できるのです。数値微分はまさにこの定義を上手に利用しています。
(b)重力加速度の値から積分して、自由落下距離の式を導きましょう。
計算の結果が具体的な物理現象ですので感覚的に納得しやすい良い課題です。また、物理で力学を勉強し始める際の定番的問題です。これが出来れば公式をおぼえる必要がありません。
重力加速度は定数 g =9.8[ m/s2 ]です。重力加速度から一定時間後の自由落下距離 s を求めるためには、2回積分を施します。加速度を時間で積分すると速度が導かれ、速度を時間で積分すると距離になるからです。
式66.24 の積分定数は例えば観測者の位置 s0 として残しても良いのですが、物理的に残す意味がないので取ってしまいました。
今回はここまで
微積分とは何か、そしてコンピュータで微積分を利用する方法、数値微分と数値積分を簡単に紹介しました。問題では、基本的な定義と公式を確認しました。次回は微分をうまく数値計算に活用した例としてニュートン・ラフソン法を紹介します。解の公式を用いずに、コンピュータの長所を生かして方程式の近似解を得ることが出来る便利な方法です。
どうぞ、お楽しみに。
今回のまとめ
微分・積分の定義を確認しました。
数値微分・数値積分とは何かを紹介しました。

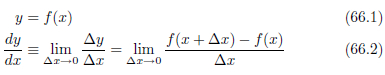
![]() は、
は、![]() と書くこともできます。簡略に表示するために、
と書くこともできます。簡略に表示するために、
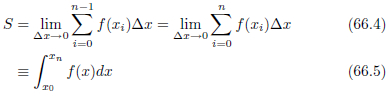

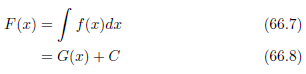
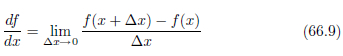
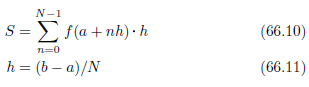
![]()







