離れたところに飛んでくるテニスボールに対して、
かつてソフトテニス部の副顧問をしていた時、
今回学習するのは、

ニュートン・ラフソン法とは
ニュートン・
ニュートン・
ニュートン・
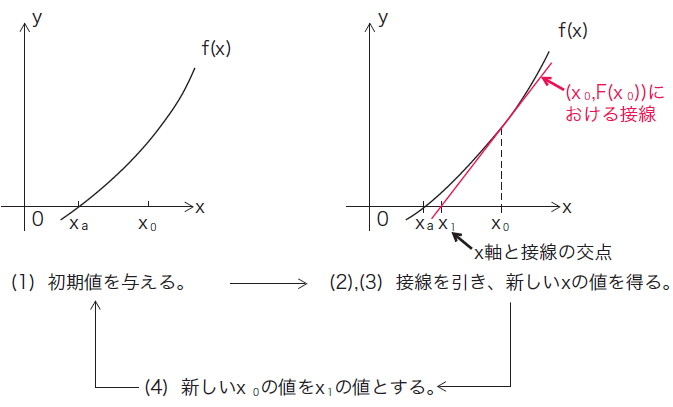
ニュートン・ラフソン法のアルゴリズム
ニュートン・ このアルゴリズムは、 ニュートン法で解を求めるためには、 学生時代は記憶することが仕事でしたが、 ニュートン・ この例題の意図するところは、 ニュートン・ 漸化式は次々と真の値に近づいていきます。理論的には、 以下はその実行結果です。 今回は、ニュートン・
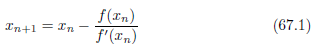
例題 f(x)=x2-2 の解をニュートン・
漸化式をたてましょう
![]() の値を計算すると言うことです。共役
の値を計算すると言うことです。共役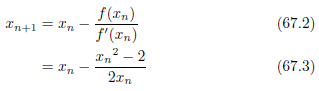
漸化式からソースコードを作成しましょう
01: //filename : NewtonMethodTest.java
02:
03: import java.io.*;
04: import java.util.*;
05: import java.lang.*;
06:
07: //-------------------------------------
08: public class NewtonMethodTest {
09:
10: //---------------------------------
11: //データ宣言部
12: static int ShokiTi=1;
13: static int Kurikaeshi=10;
14: //none
15:
16: /**
17: * メインメソッド
18: */
19: public static void main (String args []) {
20: NewtonMethod();
21: }// end of main()
22:
23:
24:
25: //---------------------------------
26: //メイン関数内で利用する関数宣言
27: //- - - - - - - - - - - - - - - - -
28: //
29: static void NewtonMethod(){
30: //float の精度で計算
31: float x_p;//漸化式の初期値
32: float x_s;//漸化式の計算結果
33: x_p = ShokiTi;
34: for(int i=0;i35: x_s = x_p - (x_p*x_p-2) / (2 * x_p);
36: System.out.println
37: (i + " : " + x_p + " -> "+ x_s );
38: if (x_s == x_p) {
39: System.out.println
40: ("精度の限界まで計算しました。");
41: break;
42: }// of if
43: x_p = x_s;
44: }// of for i
45:
46: //double の精度で計算
47: double x_p2;//漸化式の右側のx値
48: double x_s2;//漸化式の左側のx値
49: double x_p3;//確認用
50: x_p2 = ShokiTi;
51: x_p3 = ShokiTi+1;
52: for(int i=0;i<=Kurikaeshi;i++){
53: x_s2 = x_p2 - (x_p2*x_p2-2) / (2 * x_p2);
54: System.out.println
55: (i+" : " + x_p2 + " -> "+ x_s2 );
56: if ((x_s2 == x_p2) || (x_s2 == x_p3)) {
57: System.out.println
58: ("精度の限界まで計算しました。");
59: break;
60: }// of if
61: x_p3 = x_p2;
62: x_p2 = x_s2;
63: }// of for i
64: }// end of NewtonMethod
65:
66: }// end of this file...NewtonMethodTest.java0 : 1.0 -> 1.5
1 : 1.5 -> 1.4166666
2 : 1.4166666 -> 1.4142157
3 : 1.4142157 -> 1.4142135
4 : 1.4142135 -> 1.4142135
精度の限界まで計算しました。
0 : 1.0 -> 1.5
1 : 1.5 -> 1.4166666666666667
2 : 1.4166666666666667 -> 1.4142156862745099
3 : 1.4142156862745099 -> 1.4142135623746899
4 : 1.4142135623746899 -> 1.4142135623730951
5 : 1.4142135623730951 -> 1.414213562373095
6 : 1.414213562373095 -> 1.4142135623730951
精度の限界まで計算しました。今回はここまで



