これまで、
問題 関数を数値微分するプログラムを作りましょう。
前進差分と中心差分それぞれの場合で求めましょう。その際、
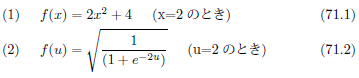
解説
問題 関数を数値微分するプログラムを作りましょう。
先ずは、
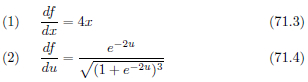
(1)
それでは早速、
01: class Forward_CentralDifference01 {
02:
03: public static double f1(double x) {
04: double a = 2;
05: double b = 4;
06: return a*Math.pow(x,2)+b;
07: }
08:
09: public static double f2(double u) {
10: return Math.sqrt(1/(1+Math.pow(Math.E,-2*u)));
11: }
12:
13: public static void main(String[] args) {
14: double x = 2;
15: double hf = Math.pow(2,-26);
16: double hc = Math.pow(2,-52);
17:
18: double fdiff1 = 0; //forward difference 前進差分
19: double cdiff1 = 0; //central difference 中心差分
20: System.out.println("f1(x) = " + f1(x));
21: System.out.println("f1(x+hf) = " + f1(x+hf));
22: fdiff1 = ( f1(x+hf) - f1(x) )/hf;
23: System.out.println("fdiff1 = " + fdiff1);
24: cdiff1 = ( f1(x+hc) - f1(x-hc) )/(2*hc);
25: System.out.println("f1(x+hc) = " + f1(x+hc));
26: System.out.println("f1(x-hc) = " + f1(x-hc));
27: System.out.println("cdiff1 = " + cdiff1);
28: System.out.println("TrueDiff = " + 4*x);
29:
30: double fdiff2 = 0;
31: double cdiff2 = 0;
32: System.out.println("f2(x) = " + f2(x));
33: System.out.println("f2(x+hf) = " + f2(x+hf));
34: fdiff2 = ( f2(x+hf) - f2(x) )/hf;
35: System.out.println("fdiff2 = " + fdiff2);
36: cdiff2 = ( f2(x+hc) - f2(x-hc) )/(2*hc);
37: System.out.println("f2(x+hc) = " + f2(x+hc));
38: System.out.println("f2(x-hc) = " + f2(x-hc));
39: System.out.println("cdiff2 = " + cdiff2);
40: System.out.println("TrueDiff = "
41: + Math.pow(Math.E,-2*x)
42: / (Math.sqrt(Math.pow(1+Math.pow(Math.E,-2*x),3))) );
43:
44: }// end of main
45: }// end of class以下はその実行結果です。
C:>java ForwardDifference01
f1(x) = 12.0
f1(x+hf) = 12.00000011920929
fdiff1 = 8.0
f1(x+hc) = 12.0
f1(x-hc) = 11.999999999999998
cdiff1 = 4.0
TrueDiff = 8.0
f2(x) = 0.9909660892472095
f2(x+hf) = 0.9909660895128037
fdiff2 = 0.017823725938796997
f2(x+hc) = 0.9909660892472095
f2(x-hc) = 0.9909660892472095
cdiff2 = 0.0
TrueDiff = 0.01782372414651308おやおや、
今回は微分値の真の値が分かりますから、
01: class ForwardDifference02 {
02:
03: public static double f1(double x) {
04: double a = 2;
05: double b = 4;
06: return a*Math.pow(x,2)+b;
07: }
08:
09: public static double f2(double u) {
10: return Math.sqrt(1/(1+Math.pow(Math.E,-2*u)));
11: }
12:
13: public static void main(String[] args) {
14: double x = 2;
15:
16: for (int i=1 ; i17: double h = Math.pow(2,-i);
18: double diff = (f1(x+h) - f1(x))/h;
19: double diffc = (f1(x+h) - f1(x-h))/(2*h);
20: System.out.println("i("+i+") : h("+h+") : diff = "
21: +diff+" : diffc = "+diffc);
22: }
23: for (int i=1 ; i24: double h = Math.pow(2,-i);
25: double diff = (f2(x+h) - f2(x))/h;
26: double diffc = (f2(x+h) - f2(x-h))/(2*h);
27: System.out.println("i("+i+") : h("+h+") : diff = "
28: +diff+" : diffc = "+diffc);
29: }
30:
31: }// end of main
32: }// end of class以下はその実行結果です。不要な部分は省略します。先ずは
(略)
i(25) : h(2.9802322387695312E-8) : diff = 8.000000059604645 : diffc = 8.0
i(26) : h(1.4901161193847656E-8) : diff = 8.0 : diffc = 8.0
(略)diffは前進差分を用いたときの数値微分値です。 i が25、
次に、
△ i(21) : h(4.76837158203125E-7) : diff = 0.01782371592707932 : diffc = 0.017823724076151848
△ i(22) : h(2.384185791015625E-7) : diff = 0.017823719885200262 : diffc = 0.017823724076151848
△ i(23) : h(1.1920928955078125E-7) : diff = 0.0178237222135067 : diffc = 0.017823724541813135
i(24) : h(5.9604644775390625E-8) : diff = 0.0178237222135067 : diffc = 0.017823723144829273
★ i(25) : h(2.9802322387695312E-8) : diff = 0.017823725938796997 : diffc = 0.017823725938796997
★ i(26) : h(1.4901161193847656E-8) : diff = 0.017823725938796997 : diffc = 0.0178237222135067
★ i(27) : h(7.450580596923828E-9) : diff = 0.017823725938796997 : diffc = 0.017823725938796997
★ i(28) : h(3.725290298461914E-9) : diff = 0.017823725938796997 : diffc = 0.017823725938796997★の部分で前進部分による数値微分値が、
これは、
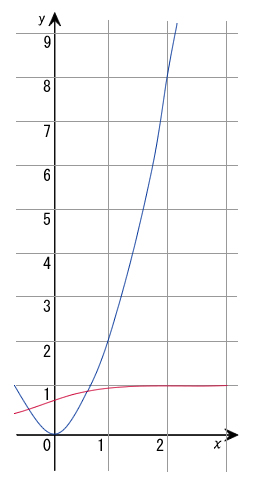
グラフ中で
実際の計算では、
今回はここまで
微少な量hについて、



