前回の問題で取り組んだ、
ドキュメントは、
なお、
解説
問題 関数を数値積分するプログラムを作りましょう。
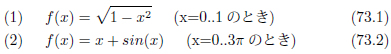
前回、
/** 数値積分(区分求積法、台形公式)の練習問題の解答例*/
class TestNumericalIntegration {
/** 問題で指定された関数の積分値を出力させる。*/
public static void main(String[] args) {
/* \int_{0}^{1} \sqrt{1-x^2} dx */
double Q1TrueVal = Math.PI*2*2/4*1/4;
System.out.println("(1) True value ="
+Q1TrueVal);
IDoubleFunction f = new f1();
Quadrature quad = new Quadrature(f);
TrapezoidalRule trap = new TrapezoidalRule(f);
double diff = 0;
/* test Illegal parameter */
//h が大きすぎる。NaN を期待。
Double testResult = quad.getResult(0.,1.,2.);
assert Double.isNaN(testResult)
: "quad.getResult(0.,1.,2.) = " + testResult;
//b<a。a,b 入れ替えして計算することを期待。。
testResult = quad.getResult(0.,-1.,Math.pow(2,-20));
assert (testResult - quad.getResult(-1.,0.,Math.pow(2,-20)) == 0 )
: "quad.getResult(0.,-1.,Math.pow(2,-20)) = " + testResult
+ " != " + quad.getResult(0.,-1.,Math.pow(2,-20));
for (int i=0;i<20;i++){
System.out.println(i+" : Quadrature diff ="
+(Q1TrueVal - quad.getResult(0.,1.,Math.pow(2,-i))));
System.out.println(i+" : Trapezoidal diff="
+(Q1TrueVal - trap.getResult(0.,1.,Math.pow(2,-i))));
}// of for
/* \int_{0}^{3\pi} (\frac{1}{2}x^2 - cos x) dx */
double Q2TrueVal = 9.0/2*Math.pow(Math.PI,2)+2;
System.out.println ("(2) True value ="+Q2TrueVal);
f = new f2();
quad = new Quadrature(f);
trap = new TrapezoidalRule(f);
for (int i=0;i<20;i++){
System.out.println(i+" : Quadrature diff ="
+(Q2TrueVal - quad.getResult(0.,3*Math.PI,Math.pow(2,-i))));
System.out.println(i+" : Trapezoidal diff="
+(Q2TrueVal - trap.getResult(0.,3*Math.PI,Math.pow(2,-i))));
}// of for
}// of main
}// end of class TestNumericalIntegration
/** 積分クラスに共通するものを用意しておく*/
class DoubleIntegration{
/** 積分開始値*/
protected Double _a;
/** 積分終了値*/
protected Double _b;
/** 区分値*/
protected Double _h;
/** 積分する関数クラスへの参照*/
IDoubleFunction _f;
/**
* 積分する関数クラスへの参照を受け取る。*/
public DoubleIntegration(IDoubleFunction f){
_f=f;
}// of DoubleIntegration
/**
* 適切な大きさ(h<=|b-a|) の正の値か。b はa より大きいか。
* @param a 積分開始値
* @param b 積分終了値
* @param h 区分値
* @return true if 適切な引数だったor
* false if 引数に不適切な値があった。
*/
protected boolean check(Double a,Double b,Double h){
_a=a;_b=b;_h=h;
if (_h<=0) return false;
if (_h > Math.abs(_b-_a)) return false;
if (_a>_b) {
Double temp=_a; _a=_b; _b=temp;
}
return true;
}// of check
}// of class DoubleIntegration
/** 区分求積法を行うクラス*/
class Quadrature extends DoubleIntegration{
/**
* @param f 積分する関数クラスへの参照
*/
public Quadrature(IDoubleFunction f){
super(f);
}// of constructor
/**
* 引数で与えた積分範囲と区分値で積分を実行し結果を返す。
* @param a 積分開始値
* @param b 積分終了値
* @param h 区分点間の距離
* @return true if 適切な引数だったor
* false if 引数に不適切な値があった。
*/
public Double getResult(Double a,Double b,Double h){
if (check(a,b,h)==false) return Double.NaN;
Double result = 0.;
Double current = _a;
while (_b>current){
result += _f.calc(current)*_h;
current += _h;
}// of while
return result;
}// of getResult
}// end of class Quadrature
/** 台形公式を使うクラス*/
class TrapezoidalRule extends DoubleIntegration{
public TrapezoidalRule(IDoubleFunction f){
super(f);
}// of constructor
public double getResult(Double a,Double b,Double h){
if (check(a,b,h)==false) return Double.NaN;
Double result = 0.;
Double current = _a;
while (_b>current){
result += (_f.calc(current)+_f.calc(current+_h))*_h/2;
current += _h;
}// of while
return result;
}// of getResult
}// end of class TrapezoidalRule
/** 倍精度実数型の引数と戻り値のメソッドを持つクラス
のためのインタフェイス*/
interface IDoubleFunction {
/** 関数計算を行うメソッドはこの名前でオーバーライドする。*/
public Double calc(Double x);
}// end of interface IDoubleFunction
/** f(x)=\sqrt{1-x^2} */
class f1 implements IDoubleFunction{
/**
* 引数に対応する関数の計算結果を返す。
* 引数に範囲があるためチェックを加えている。
* @param x
* @return 関数計算結果
*/
public Double calc(Double x){
if ((x>1)||(x<-1)) return Double.NaN;
return Math.sqrt(1-x*x);
}// of calc
}// end of class f1
/** f(x)=x+sin(x) */
class f2 implements IDoubleFunction{
public Double calc(Double x){
return x + Math.sin(x);
}// of calc
}// end of class f2コンパイルからドキュメントの生成、
javac TestNumericalIntegration.java > compile.log
javadoc *.java -d ./javadoc -private > javadoc.log
java -ea TestNumericalIntegrationバッチファイルでは、-eaオプションを付けてプログラムを実行しています。これはEnableAssertionの意味で、
以下はその実行結果です。出力の途中を少々省略します。
(1) True value =0.7853981633974483
0 : Quadrature diff =-0.21460183660255172
0 : Trapezoidal diff=0.2853981633974483
1 : Quadrature diff =-0.14761453849477102
1 : Trapezoidal diff=0.10238546150522898
(略)
18 : Quadrature diff =-1.905158201864765E-6
18 : Trapezoidal diff=2.1904413838313985E-9
19 : Quadrature diff =-9.528998897723184E-7
19 : Trapezoidal diff=7.744338503812287E-10
(2) True value =46.41321980490211
0 : Quadrature diff =-0.5419896772052653
0 : Trapezoidal diff=-5.269979121760578
1 : Quadrature diff =1.6890420259118457
1 : Trapezoidal diff=-0.6671701939727015
(略)
18 : Quadrature diff =1.77515612449497E-5
18 : Trapezoidal diff=-2.2478055683450293E-7
19 : Quadrature diff =8.763391441846125E-6
19 : Trapezoidal diff=-2.2477816941091078E-7この実行結果をみると、
クラスの継承やインターフェイスを使いましたから、
ちょっとご注意を
今回のような滑らかな関数では精度良く近似できましたが、
実用的には、
実際に数値積分を活用する場合には、
今回はここまで
数値計算の2つの方法をJava言語で実装しました。サンプルとしては少々長いソースコードでしたが、



