仕事をやり遂げるために必要な時間を見立てることが出来たら、
前回は、

計算量:バイナリサーチの場合O (log2(n))
バイナリサーチ
- [Step 1]
図75.
2の①のように、 5個の整数を格納した配列 valsから値「5」 を格納した位置(添え字の値)を検索する場合 ( target=5)を紹介します。 図75. 2 バイナリサーチとは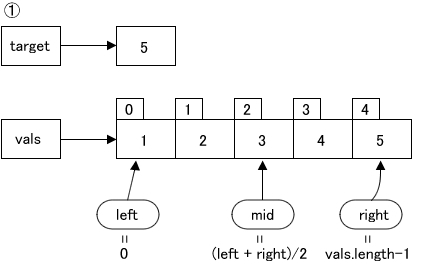
先ず検索範囲を設定します。最初ですから左端は配列の先頭要素ですので、
変数 left=0、右端は配列の末尾要素ですから変数 right=vals.となります。中央値の位置はlength-1=4 (left+right)/2=2です。もし、
中央値が目的の値ならば、 めでたく検索は終了です。しかし、 違っていれば、 中央値と目的の値の大小を比較します。もし、 中央値よりも目的の値が小さければ、 中央値以降のデータは捨ててしまいます。今回は、 中央値より目的の値が大きいので、 中央値より前のデータを捨てます。 - [Step 2]
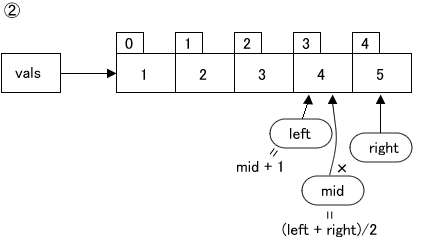
図の②のように、
Step1の操作によって、 注目する配列の範囲はn/ 2 になりました。話を簡単にするために、nの偶奇は考えません。実際にコードを組む際には、 n/ 2 を整数変数の除算として取り扱えば、小数部分が発生せず、 都合良く範囲が決まります。 新しい配列の中央の値と目的の値を比較します。等しければ検索は終了。
等しくなければ大小を比較します。中央値よりも目的の値が大きいので、
現在注目しているデータ以前を捨ててしまいます。 - [Step 3]
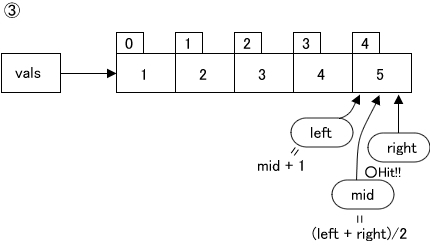
図の③のように、
Step2の操作によって、 残った配列のサイズは(n/ 2 )/2になりました。今回の場合では残りのデータは1つだけになりました。ここで探す値target=5と配列の値vals[4]=5が等しいので、めでたく検索は成功し終了です。もし、 vals[4]の値が5でなければ、探す値は配列内に存在しなかった、 ということで、 検索は失敗し終了します。検索に失敗した場合には、 -1などの、 配列の添え字としてあり得ない値を返して、 検索に失敗したことを表明しましょう。 - [Step a、
最悪の場合] 最悪の場合、
配列のサイズが1になるまでこのアルゴリズムが実行されます。繰り返しの回数aは次のような式で表されます。 
バイナリサーチの計算量 O (log2(n))
y=log2(x) のグラフとy=x のグラフを並べて描くと、
x が大きくなるほどバイナリサーチが有効なことがよく分かります。 図75. 3 y=xとy=log2xのグラフ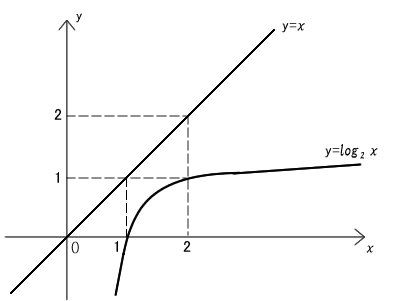
問題 バイナリサーチのプログラムを作りましょう。
前回の問題で作成したリニアサーチのコードを変更してバイナリサーチのコードを作成しましょう。最低限、execメソッドの挙動を変更することで対応できます。前回同様実行時間を計測し、
解説
問題 バイナリサーチのプログラムを作りましょう。
以下にバイナリサーチのコードを示します。お手元の環境での実行時間を計測してみてください。
01:public class BinarySearch {
02:
03: public static int exec(int[] vals, int target) {
04: int left = 0; /* start key of index */
05: int right = vals.length - 1; /* end key of index */
06: int mid; /* middle key of index */
07: while(left 08: mid = (left + right) / 2; /* calc of middle key */
09: if (vals[mid] == target) {
10: return mid;
11: } else if (vals[mid] 12: left = mid + 1; /* adjustment of left(start) key */
13: } else {
14: right = mid - 1; /* adjustment of right(end) key */
15: }
16: }
17: return -1;
18: }// end of exec
19:
20: public static void main(String[] args) {
21: int len = 100000;
22: int[] data;
23: data = new int[len];
24: for(int i=0; i<len; ++i) data[i]=i;
25: int result;
26: int repeat = 10000;
27: long time;
28: time = System.currentTimeMillis();
29: for (int i=0; i<repeat; ++i){
30: BinarySearch.exec(data,3);
31: BinarySearch.exec(data,27);
32: BinarySearch.exec(data,(int)(len/2));
33: BinarySearch.exec(data,(int)(len*2));
34: }
35: time = System.currentTimeMillis() - time;
36: System.out.println(time + "[msec]passed.");
37: }// end of main
38:
39:
40: private static void resultPrint(int result){
41: if (result != -1) {
42: System.out.println("[ Found ] index key = " + result);
43: } else {
44: System.out.println("[Not Found]");
45: }
46: }// end of resultPrint
47:
48:}// end of BinarySearch以下はその実行結果です。
C:\>java BinarySearch
16[msec]passed.私の環境
今回はここまで
次回は、



