はじめに
前回は、QoSのメタクラスを紹介しましたが、読者の方の中にはメタクラスというものに馴染みがない方も多いと思いますので、今回はメタクラスとは何かについて、QoSという抽象的な議論をひとまず置いて、より身近な例を使ったメタモデリングの具体例を通じて学びましょう(この記事は、筆者のOCRESブログでも解説しており、併せて読まれると、より理解が進むと思います)。
メタモデルはなぜ必要か?
モデルとモデリング言語の関係は、数学理論(数学モデル)と数式の関係に似ています。
次の式は、ニュートン力学の公式ですが、この公式を使った推論をすべて自然言語で行うとしたら、極めて煩雑で、場合によっては理解不能に陥ってしまいます。
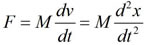
また、数式と数学理論を切り離して別々に学ぶことは極めて困難です。さらに、UMLは、数式とは異なり単なる表記法ではなく、言語自身をモデリング化したものであり、モデル自身とより密接不可分な関係にあります。
メタモデルの具体例
では、次に具体的な例を見ていきましょう。今回は、あまり細かいことを気にせず直感的な理解ができればよしとします。
図1は、メッセージ送信者-受信者モデルを表しています。送信者は情報を媒体に合わせてエンコーディングし、受信者は媒体からデコーディングを経て情報を獲得します。そして、送信者はエンコーディングするときに、自分の思惑などにより情報を変形する可能性があり、受信者はデコーディングの際、先入観などから情報を変形して受け取る可能性があります。また、媒体にはノイズが入る可能性もあります。
図1 メッセージ送信者-受信者モデル
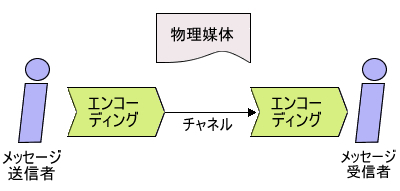
この図で示される関係は、実は、かなり広範に成立します。たとえば2人の人間同士の会話にも成立し(その場合、媒体は空気振動(音声)やボディアクションなど)、テレビ局と視聴者の間にも成り立ちます。別の言い方をすると、メタモデル的性質を持ちます。
図2は、この関係を、UMLを使ってメタモデルで表現したものです。
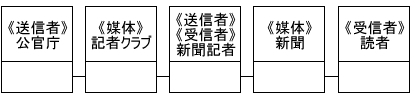
図中の四角形はすべてメタクラスを表しています。そしてこの関係を、官公庁―新聞記者、新聞記者―読者の2つにあてはめたものが図3のクラス図になります。
図2 メタモデル
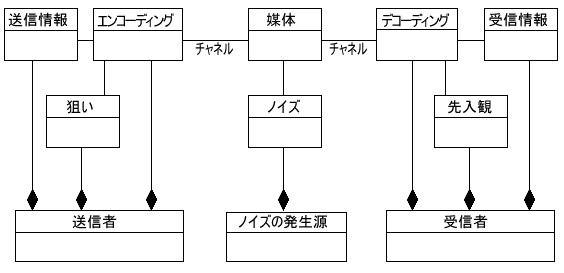 図3 クラス図(例)
図3 クラス図(例)
みなさんの中には、ソフトウェアパターンやデザインパターンの考え方に似ているな、という印象を持たれた方もいらっしゃると思います。ご推察の通り、メタモデルは、ソフトウェアパターンも表現できます。そして、それ以上のことができます。
コミュニケーション理論の観点から
ここで少し、コミュニケーション理論の観点から考察を加えてみましょう。現代社会において、ニュースの情報ソースは圧倒的に官公庁が多く、それ以外は企業などのほかの組織体やインフォーマルな個人的ソースになります。チャネルには、フォーマルなものとインフォーマルなものがあり、図中の記者クラブはどちらでしょうか? 記者クラブ自身が官公庁の中にあり、つまり税金を使って維持しているという観点からはフォーマルなチャネルですが、その排他性や、独自の内部ルールを持つという観点からは、インフォーマルなものに分類されるでしょう。
また、媒体には固有のルールがつきます。新聞などのマスメディアの例で考えましょう。
本来、国民のジャーナリストに対する期待は、チェックアンドバランスの観点から、権力組織が出したがらない情報の報道です。しかしながら、歴史的に、これは極めて危険な作業で、ご存じのように、アメリカでも謎の死を遂げたジャーナリストは数あまたいます。また暴力以外にも、訴訟リスクがつきまといます。そういった意味で、報道の自由は尊重されるべきでしょう。しかしながら、反対に個人のプライバシーは、その不可逆性(いったん外に出るともとに戻せない)と社会的生命を奪う可能性から、最大限守られる必要がありますが、その度合いは国や時代によって大きく異なります(参考までにいうと、記者クラブのような運営は、欧米にとっては奇異に映り、本来出しては行けない情報(たとえば軍事機密など)は、内部ルールではなく刑事罰などを含む国家の法律で守るべきであり、また税金で運営されているのならば、特定のマスコミではなく、全体に対してオープンであるべきだという風に考える傾向があります。また、彼らは、けっしてインフォーマルなチャネルを否定しているわけではありません)。
◇ ◇ ◇
いずれにせよ、ルールは時代や国によって大きく変わるけれど、送信者-受信者モデルは太古の昔からほとんど変わらないことが、おわかりいただけるかと思います。
システム構築のうえで、どこが頻繁に変わりどこが不変的であるかを知ることは非常に重要であり、設計上の大きな指針となります。
オブジェクト指向分析設計の利点の1つは、既存のメタモデルの利用とともに、不変部分と可変部分の発見が、従来の手法、たとえば機能構造分析に比べ極めて容易、あるいは意識的に行える点です。
![]()



![]()


