前回の掲載からしばらく間が空いてしまいましたが、
線形回帰の復習
今回は連載第8回と第9回で紹介した線形回帰を実装してみる実践編です。
まずは簡単に復習しましょう。
回帰とは、
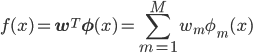 (式1)
(式1)ここでφ(x)=(φm(x))を基底関数といい、
しかし今はわかりやすさを優先して、
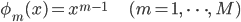 (式2)
(式2)この多項式基底を使った場合、
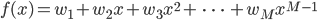 (式3)
(式3)基底関数φ(x)はこのように選んで固定しつつ、
f(x)がデータ点 (xn, tn) (n=1, ..., N) の
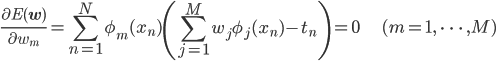
これを導くには二乗誤差やその偏微分などの理解が必要ですが、
行列を使ってこの連立方程式を整理すると、
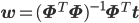 (式4)
(式4)ただし、
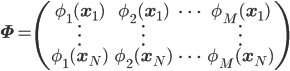 (式5)
(式5)こうして求めたパラメータwを
ちなみにM=2のときは、
実装のための準備
それでは線形回帰を実装していきましょう。
環境には、
機械学習に限らず、
そこで、
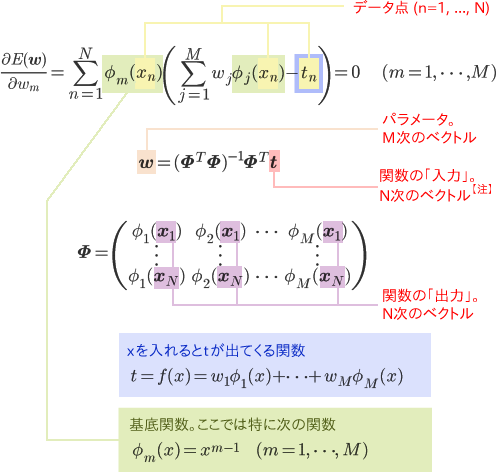
- 注
- xnがD次元空間の点の場合、
XはN×D次元の行列として与えられます。今回は簡単のためD=1としていますが、 D≧2の場合も線形回帰のアルゴリズムは同じです。
当たり前のことをわざわざ繰り返しているだけに見えるかもしれませんが、
また、
こういったことは紙の上で丁寧に確認するのがおすすめです。すべてコンピュータの上で済ませられると思ったら大間違いですよ!
線形回帰の実装
変数の形がわかったところで、
まずはnumpyとmatplotlibを利用するための宣言を書きます。
import numpy as np
import matplotlib.pyplot as pltXとtはデータでしたから、
今回は簡単のために、
X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
t = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.89, -0.79, -0.04])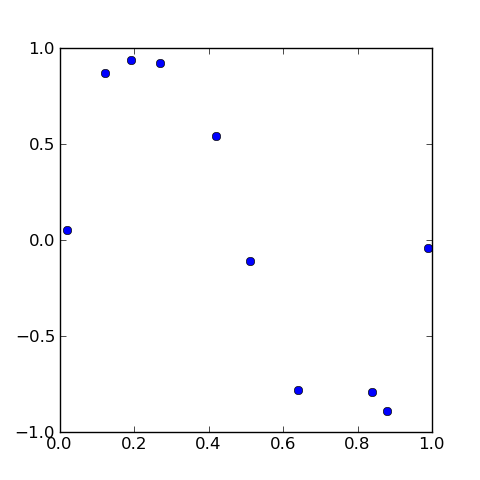
Xとtを外部のファイルから読みこむようにすれば、
次は行列Φの計算です。
まずは基底関数φ(x)にあたるものとして、 [φ1(x), φ2(x), ……, φM(x)] を返す関数phi(x)を定義しましょう。
そろそろMも決めなくてはいけませんね。ここではひとまずM=4とします。
今回は多項式基底を使うのでしたから、
def phi(x):
return [1, x, x**2, x**3]このphi(x)とXから
PHI = np.array([phi(x) for x in X])[~ for ~ in ~] というのは
phi(x)は [φ1(x), φ2(x), ……, φM(x)] を返す関数でしたから、 [phi(x) for x in X] は [φ1(xn), φ2(xn), ……, φM(xn)] が並んだ配列となります。これをnp.
# print PHI で PHI の中身を確認すると:
[[ 1.00000000e+00 2.00000000e-02 4.00000000e-04 8.00000000e-06]
[ 1.00000000e+00 1.20000000e-01 1.44000000e-02 1.72800000e-03]
[ 1.00000000e+00 1.90000000e-01 3.61000000e-02 6.85900000e-03]
[ 1.00000000e+00 2.70000000e-01 7.29000000e-02 1.96830000e-02]
[ 1.00000000e+00 4.20000000e-01 1.76400000e-01 7.40880000e-02]
[ 1.00000000e+00 5.10000000e-01 2.60100000e-01 1.32651000e-01]
[ 1.00000000e+00 6.40000000e-01 4.09600000e-01 2.62144000e-01]
[ 1.00000000e+00 8.40000000e-01 7.05600000e-01 5.92704000e-01]
[ 1.00000000e+00 8.80000000e-01 7.74400000e-01 6.81472000e-01]
[ 1.00000000e+00 9.90000000e-01 9.80100000e-01 9.70299000e-01]]最後に、
w = np.dot(np.linalg.inv(np.dot(PHI.T, PHI)), np.dot(PHI.T, t))また、
# np.linalg.solve(A, b) は A^{-1}b を返す
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t)) np.
# print w で w の中身を確認すると:
[ -0.14051447 11.51076413 -33.6161329 22.33919877]推定した関数を図示する
こうしてwを求めることができましたが、
そのためにまず
# (式 1) の場合
def f(w, x):
return np.dot(w, phi(x))# (式 3) の場合
def f(w, x):
return w[0] + w[1] * x + w[2] * (x ** 2) + w[3] * (x ** 3)どちらでもかまいませんが、
関数を曲線として描くにはpyplot.
xlist = np.arange(0, 1, 0.01)
ylist = [f(w, x) for x in xlist]
plt.plot(xlist, ylist)xlistは、
np.
ylistは、
あとはデータ点の分布を描いて、
plt.plot(X, t, 'o')最後にplt.
plt.show()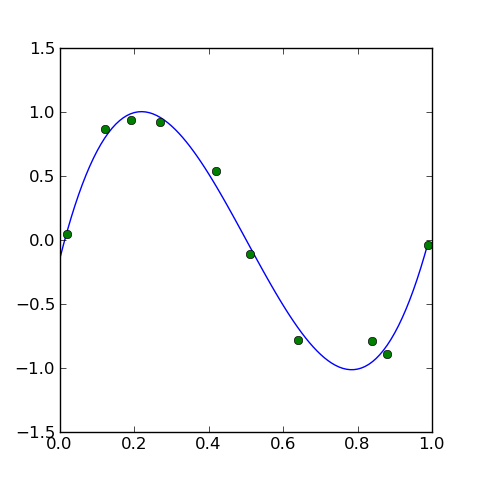
様々な条件で試す
ここまでのコードをまとめましょう。
import numpy as np
import matplotlib.pyplot as plt
X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
t = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.79, -0.89, -0.04])
def phi(x):
return [1, x, x**2, x**3]
PHI = np.array([phi(x) for x in X])
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t))
xlist = np.arange(0, 1, 0.01)
ylist = [np.dot(w, phi(x)) for x in xlist]
plt.plot(xlist, ylist)
plt.plot(X, t, 'o')
plt.show()見通しの良い短いコードですから、
例えば、
基底関数を変更する
上のコードではφ(x)の次数、
例えばM=8にするには、
あるいは、
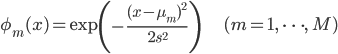
ここで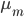 は [0, 1] 区間をM等分する点を、
は [0, 1] 区間をM等分する点を、
このように基底関数を取り替えても、
正則化項を入れる
「正則化」
実装に関係のある結果だけ説明すると、
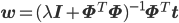
Iは単位行列、
λをいくつにするかが迷うところですが、
このように条件を少しずつ変えながら結果を確認しておくことで、
そういった蓄積は、
次回は理論編。ベイズ線形回帰を紹介します。



