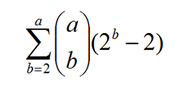いっしょによく売れる商品は、マーケティング上重要
実店舗でもECサイトでもマーケティング上、「ある商品といっしょによく売れる商品は何か?」という発想はとても重要です。
実店舗であれば、次のように商品の配置を決めるのに役立てることが考えられます。
- 「いっしょによく売れる商品をより近くに置くことで買われやすくする」
- 「もしくは意図的に遠くに置くことで、店舗内の回遊を促す」
また、次のようにセール対象商品の選定にも利用できます。
- 「セールの対象商品にはどちらか片方だけを含み、もう片方はセールに含まず通常価格で販売する」
一方、ECサイトであれば、次のようにレコメンデーションの機能につなげることができます。
このような「ある商品といっしょによく売れる商品を発見する」分析を「マーケット・バスケット分析」と呼びます。
今回は、実際に手を動かす前に理論編として、マーケット・バスケット分析、そして実際に利用する機械学習の手法について解説します。
どうすればマーケット・バスケット分析を実現できるのか
マーケット・バスケット分析は「ある商品といっしょによく売れる商品を発見する」分析です。これは捉え方を変えると、次のように言い換えることができます。
- 「ある商品が含まれる購入パターンのうち、最も頻出する購入パターンを発見する」
そのような「頻出するパターンをデータの中から発見する」分析を「頻出パターンマイニング」と呼びます。与えられた分析対象のデータのパターンを元に分析するため、教師あり学習、教師なし学習の2つの分類で考えると「教師なし学習」に属する分析手法です。
ただし、頻出する購入パターンを探し出しても、単純に最も多い購入パターンが求めている答えとは限りません。たとえば、コンビニエンスストアにおけるジュースのように、よく売れる商品は、どんな商品から見ても「よくいっしょに売れる商品」になってしまうことがあるためです。
そのため、「よくいっしょに売れる商品は、商品間に関係性がある」と考え、関係性が強い商品を探していきます。
そのような複数の事象間における関係を「アソシエーションルール(または相関ルール)」と呼びます[1]。そして、アソシエーションルールを求める分析を「アソシエーション分析」と呼びます。マーケット・バスケット分析では、このアソシエーション分析が多く用いられます。
なお、アソシエーション分析は、今回取り上げるマーケット・バスケット分析に限定される手法ではありません。事象間のアソシエーションを求める分析であれば、次のようにさまざまな状況で応用できます。
- サイトの訪問履歴から、ユーザが一度のサイト内回遊で閲覧するページの組み合わせを探し出す
- サイト内検索で同時に利用される単語を探し出す
アソシエーションルールはどのようにして求められるか
では、アソシエーションルールは具体的にどのようにして求められるのでしょうか。実際の手順を見て行く前に、基礎的な用語を把握しておきましょう。
まず、パンとミルクがいっしょに買われる場合、次のように表記するのが一般的です。
この場合の印(⇒)の左側を「条件」、右側を「結論(または帰結)」と呼びます。
また、アソシエーション分析では、今回の例における購入履歴のようなデータを「トランザクションデータ」と呼びます。
アソシエーション分析で計算する3つの値
まず、全トランザクション(全顧客による全購入履歴)を用いて、次の2つの値を計算します。
- 信頼度(confidence)
- 支持度(support)
信頼度は、「条件(パンを買う)が起きた場合に、結論(ミルクを買う)が起きる割合」を表します。これにより、条件(パンを買う)と結論(ミルクを買う)のアソシエーションの強さを表します。
信頼度の計算式は次のとおりです。
図1 信頼度の計算式

支持度は、条件(パンを買う)と結論(ミルクを買う)が同時に起こる場合が全トランザクションに占める割合を表します。
支持度が低い組み合わせは、あまり買う人がいない組み合わせであることを示します。そのため、たとえ信頼度が高くても、支持度が低い組み合わせは、アソシーエション分析では有用な答えではないと考えます。
支持度の計算式は次のとおりです。
図2 支持度の計算式

次に、結論(ミルクを買う)が条件(パンを買う)と無関係に起こっていないかどうかを計算します。先ほどのコンビニエンスストアにおけるジュースのように、よく売れる商品はどの商品から見てもよくいっしょに売れる商品になってしまう可能性があるためです。
そういった現象が起こる度合いの低さを表すのが「リフト値」です。リフト値の計算式は次のとおりです。
図3 リフト値の計算式

有効なアソシエーションルールであるためには、一般的にリフト値が1より大きい必要があります。
このように、アソシエーション分析では、信頼度、支持度、リフト値の3つの値を求めます。そしてこれら3つの値でアソシエーションルールの強さと有効性を判断します。
アソシエーションルールを求めるうえでの問題点
このようにしてアソシエーションルールを求める際、「商品の組み合わせ数が莫大になる」という問題点があります。
アソシエーション分析における組み合わせの数は、次の計算式で求めることができます。
図4 a種類における組み合わせの数
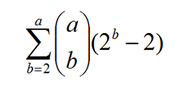
この計算式では、商品が10種類の場合は約5万7千通り、20種類の場合では約34億通りにもなります。実店舗となれば、商品の数は百種類以上となることも珍しくはなく、このような組み合わせ数を計算することは非現実的です。
これに対する解決策として、たとえば「オレンジジュース」「コーヒー」といった粒度で商品を分類するのではなく、「飲料」という粒度で商品を分類するなど、商品分類の粒度を変更することで組み合わせ数を減らす対応が考えられます。しかし、この方法では分析の精度が落ちてしまいます。
効率的に計算するための「アプリオリアルゴリズム」とは
上記の問題を解決するには、すべての組み合わせを試すことなく、より効率的にアソシエーションルールを計算することが必要になります。そのために広く利用されているのが「アプリオリアルゴリズム」です。
例として、商品がミルク、チーズ、バター、パンの4つの場合において、ミルクと最もよくいっしょに売れる商品を探す場合を考えてみましょう。
この場合の総組み合わせは、次のようになります。
- ミルク、チーズ
- ミルク、バター
- ミルク、パン
- ミルク、チーズ、バター
- ミルク、チーズ、パン
- ミルク、バター、パン
- ミルク、チーズ、バター、パン
アプリオリアルゴリズムは、計算量を減らすために、「最低支持度」と呼ばれる値を設定するのが特徴です。仮に今回は「0.3」に設定したとします。
アプリオリアルゴリズムでは、まず、全トランザクションデータから最小組み合わせの支持度を計算します。今回の例では、次の値だったとしましょう。
- 支持度(ミルク ⇒ チーズ) = 0.5
- 支持度(ミルク ⇒ バター) = 0.2
- 支持度(ミルク ⇒ パン) = 0.6
この場合、「ミルク、バター」の支持度が0.2で、最低支持度の0.3に満たないため、「ミルク、バター」は計算対象から除外されます。しかし、この際、除外される組み合わせは「ミルク、バター」の組み合わせだけでなく、「ミルク、チーズ、バター」など、「ミルク、バター」を含むすべての組み合わせが除外されます。
これは、ある組み合わせの支持度が、その組み合わせが含まれるすべての組み合わせの数で計算されているためです。
たとえば「ミルク、バター」の場合、「ミルク、バター」という組み合わせの数だけでなく、「ミルク、チーズ、バター」など、「ミルク、バター」を含むすべての組み合わせの数で計算されます。そのため、「ミルク、バター」の支持度よりも、「ミルク、バター」を含むその他の組み合わせの支持度が大きくなることはありません。
よって、「ミルク、バター」の支持度が最低支持度を満たさない時点で、「ミルク、バター」を含むすべての組み合わせが最低支持度を満たさないことになります。
このような性質を「逆単調性」と呼びます。アプリオリアルゴリズムはこの逆単調性を利用することで、計算が必要な組み合わせ数を減少させるのです。
ミルクと商品1つの組み合わせの支持度を求めた次は、ミルクと商品2つの組み合わせの支持度を求めます。その際、すでに除外されている組み合わせは計算の対象外となります。
商品2つの組み合わせの場合においても、最低支持度に満たない組み合わせと、それを含む組み合わせを除外します。そして、その次はミルクと商品3つの組み合わせ……といったように組み合わせる商品の数を増やしていき、最終的にすべての組み合わせの数を計算します。
このようにして、アプリオリアルゴリズムは計算する組み合わせの数を減らし、現実的な計算を可能にするのです。
現在では、アプリオリアルゴリズムを改良し、より高速に計算可能なアルゴリズムがいくつか提案されています。そのうちの1つに、「FP-Growth」というアルゴリズムがあります。Mahoutは、このFP-Growthを実装しています。
次回は実践編として、実際にMahoutを利用して、FP-Growthによってマーケット・バスケット分析をしてみます。