はじめに
前回、前々回と転置索引の論理的構造について見てきました。今回は、転置索引の具体的なデータ構造や実装について説明していきます。
辞書の実装
辞書は通常、単語に対応した情報を高速に取得するために、ハッシュや木構造などのデータ構造を取ります。現在は, 安定した性能や単語の順序関係を利用したいなどの理由で、木構造のデータ構造が使われることが多いと思います。最も単純な場合、2分探索木(Binary Search Tree)や2分探索(Binary Search)の実装が考えられます。
2分探索(木)による辞書の実装
では、辞書の具体的なデータ構造について、図を交えて解説していきましょう。
前回も触れましたが、辞書には単語とその単語に対応するポスティングリストの位置情報のペア(のリスト)が格納されています。単語で検索をするので、ペア自体は単語をキーとして並び換えられます。
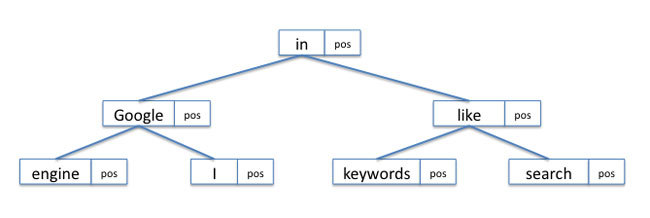
たとえば, 前回の例の文書における辞書をメモリ上で2分探索木として実装する場合は図1のようになります(各ノード間はポインタによりリンクされます)。
文書1(D1): I like search engines.
文書2(D2): I search keywords in Google.
図1 文書1、文書2に対するメモリ上での辞書の実装(2分探索木)
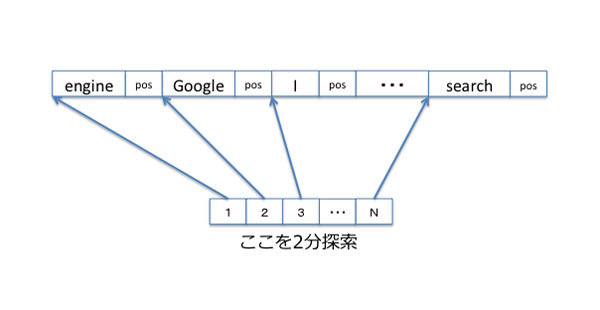
また、ディスク上に実装する場合は、ペアを単語の辞書順に並べます。ただ、単純に並べただけなので、どこがペア間の区切れかがわかるように、各ペアに対して先頭からのオフセットを保持しておき、検索時はそのオフセットの配列に対して2分探索を行うことになります(図2)。
図2 ディスク上での辞書の実装(整列した単語リストに対する2分探索)
辞書を全部メモリ上に載せることができる場合は、このような2分木は非常に高速になり、特に木がバランスされている場合は、O(log2N)回の探索で結果を見つけることができます。しかし、辞書をメモリに載せない場合(または載らない場合)はHDDなどの二次記憶装置に置く必要があり、上記のような2分探索は効率的ではありません。
HDDやSSDなどの二次記憶装置はブロックデバイスと呼ばれ、ブロック単位でI/Oが発行されます[1]。つまり、ブロック中の1ビットを読むだけでも、そのブロック全体がディスクからメモリに転送されてしまいます。
たとえば、100万件の単語辞書がある場合、2分探索では最低でも20回程度の探索が必要ですが、最悪の場合20ブロックの読み込みが必要となってしまい、1回の探索でディスクI/Oだけでも数10ms~数100msの時間がかかってしまいます。仮に、データ転送時間を3ms/ブロックとすると、ディスクI/Oだけで60msもの時間がかかってしまうことになります。
このため、大きな辞書を保持する場合には、よりブロックデバイスの特性に合ったB+木などの木構造データが使われます。
B+木による辞書の実装
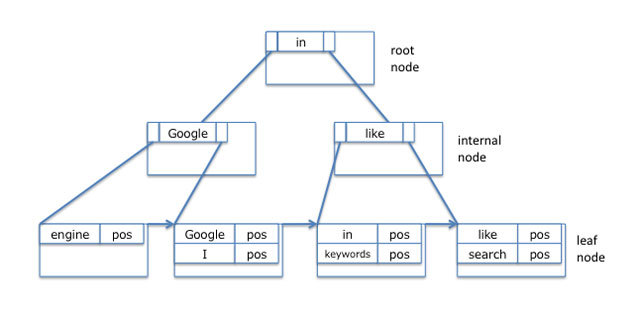
B+木はB木から派生したデータ構造です。全てのレコードは木の葉ノード(leaf node)に格納され、内部ノード(internal node)にはキーのみが格納される木構造となります[2]。
B+木は、各ノードをページと呼ばれる単位で管理し、通常はそれをファイルシステムのブロックサイズの定数倍にします。そして、そのページをノードとして木構造を構築することで、検索や構築におけるディスクI/Oを少なくするという仕組みです(図3)。ここでは、概要のみの説明とし、詳しい仕組みは参考文献を参照ください。
図3 B+木
先ほどと同様に、100万件の単語辞書がB+木で管理されているとしましょう。ここでは、ブロックサイズとページサイズは共に4Kバイトとします。また、各単語の平均サイズを10バイトとし、ページ内でのオフセットのサイズを2バイト[3]、下段ノードへの参照ポインタのサイズを4バイトとすると、単語ごとに16バイトがページ内で使われます。よって、ページには約250のキー(単語)が格納できることになります[4]。
各ページに250の単語が格納でき、ページ内の各単語に対して、その単語より小さい単語集合のノード(または大きい単語のノードが)にリンクが張られるため、100万件の単語の格納には、3段のノードがあれば十分となります(250×250×250=約1500万)。つまり、3つのブロックの読み込みで、いずれの単語も検索することが可能となります。仮に先の例と同様3ms/ブロックとすると、ディスクI/Oは9msとなり、上の例の60msと比較すると違いは歴然です。
このように、大規模な辞書をブロックデバイス上で扱う場合は、B+木を利用することで効率的に管理することができます。
転置リストの実装
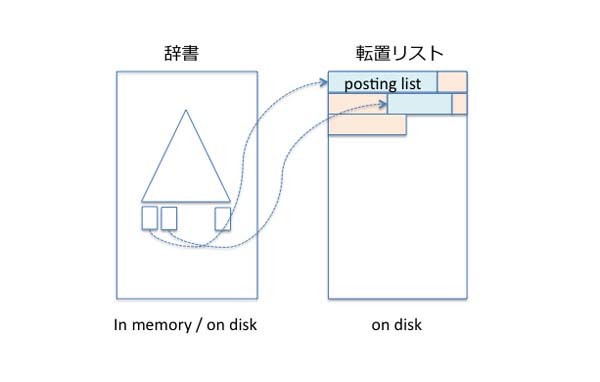
転置リストは、各単語におけるポスティングリストの集まりであり、これらは通常辞書とは別の領域(ファイル)に保存されます。
そこでは、各リストは隣りあって格納され、辞書がそのリストへの(オフセットなどの)位置情報を保持しているという構造となります(図4)。
図4 転置リストの実装
ポスティングリストは各単語ごとに数100バイト~数Mバイト、大規模な場合は数10Mバイト~数100Mバイトにもなります。よって、通常ポスティングリストはディスク上に格納され、パフォーマンスの観点から、リストはディスクの連続した領域に格納されることが多いようです[3]。こうすれば、ポスティングリストの取り出しが、1回のシークと1回の連続ディスク読み取りで行うことができるからです。
ポスティングリストの物理的な格納方法
前回説明しましたが、単語レベルのポスティングリストは、文書ID(DocID)と文書におけるオフセットのリスト(off1, off2 ...)からなります。また、各文書における出現数(オフセットの数)も保持されます[4]。ポスティングリストのこれらの情報は全て数値で表現されているので、ディスクなどに格納する場合は、多くの場合、整数のバイナリ表現としてそのまま格納します。
たとえば、各ポスティングを
DocID,freq,off1,off2,off3
のように格納する場合(','は区切れを示すために便宜的に書いています)、前回作成した"search"に対するポスティングリスト(D1:3,D2:2)は、以下のような整数列として表現されます。
1,1,3,2,1,2
この各整数をそのまま4バイトのバイナリで保存するとすると、このポスティングリストは24バイト(4バイト×6)のバイナリ列となります。
ポスティングリストの圧縮
転置リストを構成する各ポスティングリストは、検索したい文書数が増えるほど長くなります。よって、中規模以上の文書におけるポスティングリストでは、その取得におけるディスクI/Oが検索処理において非常に大きな比重を占めてしまいます。
この問題に対処するために、通常ポスティングリストは圧縮して格納され、ディスクI/Oの削減を図ります。圧縮手法にもよりますが、ポスティングリストを圧縮することにより、索引構築と検索の両方でディスクI/Oの削減による高速化が見込めます。
詳しい圧縮手法については今後の連載で説明する予定ですが、ポスティングリストは整数列となるため、整数列に向いた圧縮手法が用いられます。
まとめ
若干駆け足でしたが、転置索引の実装を辞書と転置リストに分けて説明しました。辞書は順序をもった木構造などの構造となり、転置リストは整数列のバイナリ表現となります。これらの構造は用途やユースケースによって異なりますが、基本的の部分は変わりません。
参考文献






