はじめに

今回からは、近年の話題や少し発展した話題について触れていく予定です。

第7回では、転置索引の静的な構築方法について触れました。今回は、索引に対して文書のインクリメンタルに追加していく方法について触れていきます。

動的な索引構築の必要性

第7回の復習になりますが、索引の構築方法には"静的"な方法と"動的"な方法が存在します。英語ではそれぞれ、Offline Index Construction、Online Index Constructionと呼ばれています[1]⁠。

文書が頻繁に追加される場合や索引が大規模な場合、文書の追加の度に索引を作り直すことは非常に高コストとなり現実的ではありません。このような場合は、動的な構築方法により索引をインクリメンタルに更新していくことで対応することができます。情報が絶えず追加されている近年のWeb上では、とても重要な構築方法となります。

メモリ上の索引とディスク上の索引

動的な構築において、既存の索引に新しい文書を追加することは、文書が含む単語数分の新しいポスティングを転置リスト追加することを意味します。通常、1つの文書は数百から数千の単語を保持しているので、各単語のポスティングリストの更新の度にディスク上でシークを行うことになるため、非常にコストが高い処理となってしまいます。

このため、動的な索引構築においてはメモリ上の索引とディスク上の索引の2つの索引を保持し、直近の文書はメモリ上の索引に対して更新し、そのメモリ上の索引を定期的にディスク上の索引と統合するという処理が行われます。この方法は、多くのランダムアクセス処理はメモリ上で行われるため効率的になります。これにより、検索においてはメモリ上の転置リストとディスク上の転置リストを論理的に連結しなければいけないため、検索処理は多少複雑になります。

索引の統合

動的な索引構築においては、メモリ上の索引とディスク上の索引をどのように統合するかがポイントとなります。

大きく分けて以下の2種類の統合方法が存在します。

• インプレイスな更新による統合（Inplace Index Maintenance）
• マージによる統合（Merge-based Index Maintenance）

インプレイスな更新による統合とは、新しいポスティングを既存の転置リストの最後に書き加えることにより、各ステージにおける索引への変更を最小に抑える戦略になります。各ポスティングリストに対して多めに領域を確保しておき、その領域に新しいポスティングを格納します。確保してある領域が埋まってしまった場合は、そのポスティングリストを別の領域に移動することで対応します（別の領域においても多めの領域を確保します⁠）⁠。

この方法は、データベースにおける一般的なデータ管理方法であり、従来は主要な方法となっていました。しかし、更新における統合操作はディスクにおいて大量のシークやデータの移動が発生するため、近年はもう一方のマージによる統合方法がより効率的であると考えられています。

マージによる統合

マージによる統合では、インプレイスな更新による統合とは異なり、既存のディスク上索引を直接更新することはせず、ディスク上の既存の索引とメモリ上の新しい索引をマージし、それをディスク上の新しい領域に書き出す方法となります[2]⁠。このようなマージによる索引の統合には、幾つかのマージ戦略が考えられていますので、基本的な戦略を紹介します。

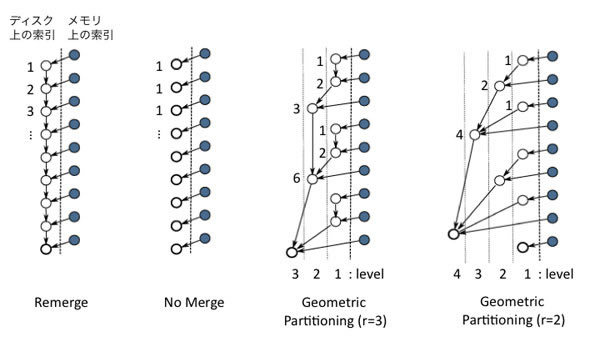
以下で紹介する3つのマージ戦略の概念図を図1に示します。図1は、各戦略における索引のマージ過程を表し、メモリ上の索引（青丸）がディスク上の索引（白丸）とどのようにマージされるかを示しています（白丸の左の数値は、メモリ上の索引を1としたときのサイズとなります⁠）⁠。

Remerge（Immediate Merge）戦略

Remerge戦略は、ディスク上の索引を常に1つに保つようにマージしていく方法となります。よって、メモリ上の索引のサイズがある閾値に達した場合、メモリ上のポスティングは既存のディスク上の索引とマージされ、新しい索引を作成します。その後、マージ元のディスク上の索引とメモリ上の索引は削除されます。

この戦略では、転置リストの取得に必要なディスクシークの数を最小化していますが、マージの度にディスク上の索引を全スキャンする必要あるという欠点があります。nを構築する総ポスティング数、bをバッファで保持できるポスティング数とすると、n/bは構築完了までのディスクへの書き出し回数を表し、n個のポスティングはn/b回のマージを行うため、構築におけるディスク操作の漸近的時間計算量は、O(n2/b) となります。

No Merge戦略

No Merge戦略は、その名のごとくマージ操作を全く行いません[3]⁠。Remerge戦略と同様に、メモリ上の索引のサイズがある閾値に達した場合、その索引はディスク上に書き出されます。

この戦略では、高いインデックス構築速度を達成しますが、ディスク上の索引が複数の索引に分割されているため、転置リストの取得に部分索引の数のディスクシークが発生してしまう欠点があります。n個のポスティングはそれぞれ1回のフラッシュを行うため、構築におけるディスク操作の漸近的時間計算量はO(n)となります。

Geometric Partitioning戦略

上記に紹介した2つのマージ戦略の中間的な方法が、Geometric Partitioning戦略となります。メモリ上に構築された索引は、毎回ではなく定期的にディスク上の索引とマージされます。Geometric Partitioning戦略では、索引を制限された数のパーティションに分割します。

この戦略では、キーとなるパラメータrを導入し（通常はr=2 or r=3）し、rによりマージのタイミングを調整します。各レベルk（k=1、2、3 ...）のパーティションは、空またはr^(k-1)・b個以上(r-1)r^(k-1)・b個以下のポスティングを保持します（kが大きいレベルになるにつれて、索引が大きくなります⁠）⁠。

メモリ上に構築された索引は常にレベル1の索引とマージされ（レベル1に索引が無い場合は書き出されるだけ⁠）⁠、ポスティング数がレベルの上限を越えた場合は、さらに1つ上のレベルの索引とのマージ処理が行われます（各レベルの上限に収まるまで繰り返しマージされます。（⁠※4⁠）⁠）⁠。

少し動作が複雑なので、具体的にr=2の場合を考えてみましょう。r=2の場合には、2進数に1を加算していくのと同じ過程でマージ処理が行われます。各桁がレベルに相当し、上のレベルの索引とのマージ処理は繰り上げに相当します。

たとえば、レベル3に索引がある場合は、00000100という2進数で表現できます。この状態に新たにメモリ上の索引をマージしていきましょう。->をマージ処理とすると、Geometric Partitioning (r=2) では以下のように索引が構築されます。

• 00000100 -> 00000101 -> 00000111 -> 00001000 -> …

r=2の場合、n個のポスティングはlog2(n/b)回のマージを行うため、構築におけるディスク操作の漸近的時間計算量は、O(n log(n/b))となります。そして, 各状態でのディスク上の索引数は1の数を数えれば求まります。また, Geometric Partitioning（r=2）はLogarithmic Mergeとも呼ばれます。r=3の場合も、パラメータが異なるだけで、同様の構築過程となります。

各戦略のまとめ

3つのマージ戦略を紹介しました。

各マージ戦略には一長一短ですが、現在は構築速度と検索速度のバランスからGeometric Partitioning戦略が有効であると考えられています。

以下に各マージ戦略の特徴を表にまとめます。

まとめ

動的な索引構築方法について説明しました。

基本としては、メモリ上の索引とディスク上の索引を分けて管理し、直近の文書の追加による索引の更新はメモリ上に索引に対して行うことで、ディスクにおけるランダムアクセスの数を減らすことにより実現します。

メモリ上の索引は定期的にディスク上の索引と統合され、近年はディスク上の索引を直接更新しないマージによる統合が主流となっています。また、マージによる統合における幾つかのマージ戦略も紹介しました。これらの戦略は毎年のように改良案が出されるなど、研究分野としても注目されています。

参考文献

• ［1］Efficient online index construction for text databases, Nicholas Lester, Alistair Moffat, Justin Zobel, ACM Transactions on Database Systems (TODS), 2008
• ［2］Inverted files for text search engines, Justin Zobel, Alistair Moffat, ACM Computing Surveys (CSUR), 2006
• ［3］Introduction to Information Retrieval, C. D. Manning, P. Raghavan, H. Schutze, Cambridge University Press, 2008