gihyo.jpサイトのロゴ

検索エンジンはいかにして動くのか？

第11回転置索引の圧縮

2010-04-06

はじめに

第2回で、索引は多くの場合圧縮されていることに言及しました。また第7回では、索引構築時にどの部分で索引を圧縮すればよいかを疑似コードを用いて説明しました。今回は、転置索引の具体的な圧縮方法について説明していきます。

圧縮の目的

中規模から大規模な索引の場合、転置リストは非常に長くなり、検索時にはディスクからの大量のデータの読み取りが行われます。転置索引（を用いた検索エンジン）では、これによる検索処理時間の増加を防ぐために、転置リストを圧縮しディスクからの読み込み時間の短縮を図ります。

この場合、圧縮された転置リストをディスクから読み込みさらに復元処理を行う必要がありますが、通常は次のようになります。

圧縮転置リストのディスクからの読み込み時間＋復元処理時間 ＜ 非圧縮転置リストのディスクからの読み込み処理

これは、近年のCPUとディスクの速度差が大きいため、主にCPUにおける処理である復元処理が高速に行えることによるものです。よって、圧縮というと容量を節約の意図で使うことが多いと思いますが、転置索引では"高速化"が主な目的となります。

転置索引の圧縮

転置索引は辞書と転置リストからなるため、転置索引の圧縮にも「辞書の圧縮」と「転置リストの圧縮」がそれぞれあります。

辞書の圧縮

辞書はタームのリストであるため、辞書の圧縮ではこのタームのリストをどうやって少ない情報で表現するかということになります。

たとえば、タームを辞書順に並べたとき、共通の接頭辞を持つタームの連続が出現する場合がありますが、その共通部分を重複して保存しないようにすれば容量の節約が図れます。しかし、通常の辞書のサイズは転置リストのサイズと比べて非常に小さいため、辞書の圧縮による転置索引全体への貢献は非常に小さいものとなります。このため、本連載では辞書の圧縮方法は扱わず、参考文献[3]にその説明を譲りたいと思います[1]⁠。

転置リストの圧縮

転置リストは文書ID、文書内のターム出現頻度（TF⁠）⁠、文書内オフセットなどからなる整数の列となります。よって、転置リストの圧縮とは、この整数列を少ない情報で表現することになります。

この整数列ですが、ランダムに整数が並んでいるわけではなく、文書IDや文書内オフセットは通常は昇順に並んでいますし、TFも通常は小さい整数となります。たとえば、文書IDが昇順に並んでいる場合、文書IDの整数をそのまま表現するよりも、1つ前の文書IDとの差分を取った方が数値としては小さい値として表現できます。また、TFのようにあらかじめ小さい数が来ることがわかっている場合は、小さい数をより小さい情報量で表現できる方法により、小さい領域で保存可能かもしれません。

このように、転置リストの圧縮では予め得られる情報に基づき圧縮を実現します。

転置リストの圧縮

ここでは、転置リストの具体的な圧縮方法を説明していきます.

通常、"整数"というと32ビット整数や16ビット整数などの固定長表現が考えられます。転置リストにおける整数列においてもこのような固定長表現の利用が考えられますが、10や100を表現するのに32ビットも使うというのは少し（かなり？）無駄な気がします。また、せっかく文書IDの差分などにより小さい数値で表現できても、固定長で表現する場合は意味がなくなってしまいます。よって、転置リストにおいては可変長符号による整数表現が使われます。

以下に、転置リストで使われるいくつかの可変長符号化方法を紹介します。

unary符号

unary符号は最もシンプルであり、整数値x（> 0）をx-1個の"1"ビットと末尾の"0"ビットで表現する符号化方法です。

たとえば、x=10の場合は "1111111110" となります。

gamma符号、delta符号

gamma符号は、整数値x（> 0）を2e + d（e = log2x, 0 ≤ d < 2e）で表現し、e+1をunary符号で、dをeビットバイナリ符号で表現する符号化方法です。

たとえば、x=10の場合、log210 = 3となるため、3＋1＝4をunary表現すると"1110"、10-23=2を3ビットバイナリで表現すると"010"となるため、それらを足した"1110" + "010" = "1110010" となります。

delta符号は、gamma符号でunaryで符号化する部分をgamma符号で置き換えたものとなります。

variable-byte符号（byte-aligned符号）

variable-byte符号は、その名の通り"複数のバイト"で符号化する方法となります。各バイトの下位7ビットを使って数値を表現し、その整数が次のバイトも含むかどうかを最上位ビット（1かどうか）で表す符号化方法です。つまり、1バイトでは27ビット、2バイトでは214ビット、3バイトでは221ビットまで表現できることになります。

たとえば、x=10の場合、x < 27 なので1バイトで表現できるので、"10001010" となります。

x=1030の場合は、x < 211なので2バイトで表現でき、
"00000100:10000110" となります。

delta符号、gamma符号などはビットレベルで符号化するため、高い圧縮率が達成できますが、その分ビット操作により復号が若干遅くなるという欠点もあります。一方variable-byte符号はバイトレベルで符号化するため、圧縮率はそれほど高くはありませんが、復号は高速に行えます。

また、これらの符号化方法は、パラメータなしの符号化方法（Parameterless Codes）と呼ばれています。なぜなら、対象とする整数列の特性に関係なく整数を符号化するからです。しかし、全体の文書数と各ポスティングリストに含まれる文書数（DF）がわかる場合[2]⁠、各文書IDの数値をある程度見積もることができ、そのポスティングリストの特性に応じて符号化を適応させることが可能となります。

次に、そのような符号化手法であるgolomn符号、rice符号を紹介します。

golomn符号、rice符号

golomn符号は、パラメータm（≥ 1）を用いて、整数値x（> 0）を、b*q+r+1（0 ≤ r < b）で表現し、q+1をunary符号、rを以下に従って符号化する方法です。

e = log2b（切り上げ⁠）⁠、g = 2e - bとし、0 ≤ r < gの場合はrをe-1ビットのバイナリ符号で、g≤ r < bの場合はr+gをe ビットのバイナリ符号で表します。

たとえば、x=10の場合、10 = 5・1 + 4 + 1 (q=1、r=4)となり、

  • e = log25 ≒ 3
    g=2e - b= 23 - 5 = 3 (< r)

となるため、q+1（2）のunary符号 + r（4）+g（3）のe（3）ビットバイナリ符号で"10:111" となります。

golomu符号はm=1の時はunary符号となり、m=2k（k=1,2,3...）の時はrice符号と呼ばれます。

なぜ圧縮できるのか？

前のセクションで、転置リストの圧縮では予め得られる情報に基づき圧縮をすると説明しました。あらかじめデータ列の情報が得られるとなぜ圧縮できるのでしょうか？ 簡単な例で説明したいと思います。

4種類の数字（1,2,3,4）がある場合、これを0,1で表すと2ビットで表すことができ、割り当ては以下のように適当に決めることとします。

  • 1：00
  • 2：01
  • 3：10
  • 4：11

このとき、[1,3,1,1]という数値の列は

  • 2（ビット）* 4（個）=8ビット

で表現できることになります。たとえば、1が出現する確率が他のものよりも高く、70％の確率で出現すると予めわかっている場合、以下のように高く出現する数値により小さいビット表現を割り当てたとします。

  • 1：0
  • 2：100
  • 3：101
  • 4：110

このとき、同様に[1,3,1,1]という数値の列は

  • 1（ビット）*3（個）+3（ビット）*1（個）= 6ビット

で表現できます。上の場合と比べて2ビットも小さく同じ数値列を表現することができました。圧縮でやっていることもこれと全く同じになります。

ポスティングリストの整数列はある分布により並んでいると考えることができます（どんな分布かはわかりません⁠）⁠。上で紹介した各符号化はその整数列に対してある予測を立てて圧縮を試みます。つまり、各符号化はある確率分布を仮定して圧縮しているということになります。

たとえば、gamma符号を見てみましょう。gamma符号は、整数xをunary符号部を 1+log2xビットとバイナリ部分を log2xビットで表現するため、

  • lx = 1 + 2log2x

ビットで表現できることになります。

整数xの符号長がわかると、シャノンの情報量の定義より[3]

  • lx = -log Pr[x]
    Pr[x] = 2-lx
    Prgamma[x] ≒ 2-(1+2logx)
    = 1/2x2

となり、これはgamma符号が暗黙的に持つ確率分布となります。つまり、gamma符号では、各整数値xが1/2x2の確率で出現すると仮定して符号化を行うということになります。

他の符号化手法も同様に暗黙的に確率分布を持ち、符号化手法の確率分布と実際の整数列の分布が近ければ近いほど、高い圧縮率が達成されます[4]⁠。

近年の圧縮手法

上記で紹介した以外にも、近年までにさまざまな高い圧縮率を誇るアルゴリズムが開発されてきました。

検索エンジンでは検索速度が一番重要である一方、高い圧縮率の符号化方法はディスクからの読み取り時間は短縮されるものの、復号時間が掛かりすぎてしまうという問題がありました。それにより、現実的には圧縮率はそこそこで復号が高速なvariable byte符号などが広く使われて来ました。しかし近年、圧縮率を高く保ちつつ復号も高速に行うことが可能が圧縮方法がいくつか開発されました。ここでは、そのうちの2つを紹介したいと思います。

Simple9（S9）

Simple9では、32ビットに可能な限りの整数を格納することで圧縮を実現します。このため、32ビットを上位4ビットと下位28ビットに分け、上位4ビットには何ビットの整数を何個格納するのかを表す9通りのステータスのどれかを、下位28ビットには実際のデータを格納します。

28ビットの具体的な分割パターンは、28ビット*1個、14ビット*2個、9ビット*3個、7ビット*4個、5ビット*5個、4ビット*7個、3ビット*9個、2ビット*14個、1ビット*28個の9通りとなります。たとえば、7つの整数列がすべて16以下であるなら、4ビット*7個のパターンが選択され、7つの整数を32ビットで表すことができます。符号化を行う場合は、整数列を先頭から見ていきどのパターンに当てはまるかを判定します。

復号はこの9通りのビットオペレーションをハードコードしておき、上位4ビットからパターンを読み込み該当のコードを実行します。復号が高速に実行できる理由としては、ビットオペレーションをハードコードしておくことや、固定長ビットの復号が分岐なしに行えることなどが挙げられます。

PForDelta

PForDeltaは近年Zukowskiら（参考文献[4]）により提案された非常に注目された手法です。その後、Yanら（参考文献[5]）により改良されました。改良案は有効であると考えられ今後の広まりが予想されますので、今回はこの改良案を紹介します（[5]ではこの改良案をNewPFDと呼んでいます⁠）⁠。

PForDeltaの考え方はS9と同様であり、複数の整数を固定長ビット配列に押し込むという方法ですが、より多くの整数を詰め込むところが違っています。

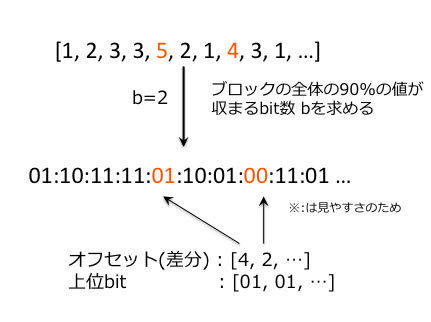
まず、整数列を32の倍数（ここでは128）個ごとに分割し、各ブロックの全体の90％の値が収まるビット数を求めます。そして、bビット * 128個の配列（配列a）に各値を詰め込みます。もちろん10％程度はbビットに収まりきらないため、これらは例外として扱います。例外である数値は、128個の配列には下位bビットのみを保存し、上位ビットは別配列（配列b）に格納することにより対応します。

また、どの部分が例外であったかも別の配列(配列c)に格納しておく必要があります。さらに、配列bと配列cはS9などの別の符号化手法により圧縮することができます。図1に具体的な数値例におけるPForDeltaの符号化方法を示します。

図1　PForDeltaによる符号化例
図1　PForDeltaによる符号化例

PForDeltaの特徴は、復号が非常に高速な点です。[3]の論文で紹介されている復号方法をリスト1に示します。復号は2段階で行われ、2つのループが実行されます。1つめのループでは、bの値に基づき各整数を復号し、2つ目のループでは、例外に対して上位ビットの補完をします（リスト1は、オリジナルのPForDeltaであるため、LOOP2内の処理内容が異なります⁠）⁠。これら各ループ内の処理は独立であるためコンパイラによるloop-unrollingが期待でき、また、ループ内で分岐が一切発生しないためSuper-Scalar CPUにおけるパイプラインがフラッシュされずに実行されるため、非常に高速に実行されます。

この処理を1つのループ（1段階）で行うことは可能ですが、上述のことから得られる利益の方が大きいため2段階で実行します。

リスト1
int Decompress<ANY>( int n, int b,
    ANY *__restrict__ output,
    void *__restrict__ input,
    ANY *__restrict__ exception,
    int *next_exception )
{
    int next, code[n], cur = *next_exception;
    UNPACK[b](code, input, n); /* bit-unpack the values */
    /* LOOP1: decode regardless */
    for(int i=0; i<n; i++) {
        output[i] = DECODE(code[i]);
    }
    /* LOOP2: patch it up */
    for(int i=1; cur < n; i++, cur = next) {
        next = cur + output[cur] + 1;
        output[cur] = exception[-i];
    }
    *next_exception = cur - n;
    return i;
}

各符号化方法について

Zhangらは参考文献[6]で、転置リストにおける各符号化方法の比較をしています。データセットにも依存するので一概には言えませんが、圧縮率に関しては、

  • rice > PForDelta > S9 > variable-byte符号

となり、復号速度は、

  • PForDelta > S9 > variable-byte符号 > rice符号

という結果となっています.

PForDeltaやS9がvariable-byte符号よりもどちらも優っていますが、実装の容易性やインクリメンタルに符号化できるなどのメリットがあるため、variable-byte符号がもう必要ないということにはならないと思われます。

まとめ

転置リストにおけるさまざまな圧縮方法を紹介しました。

各符号化方法はそれぞれトレードオフの関係にあるため、用途に応じて使いわける必要があります。また、近年は高い圧縮率かつ高速な復号処理を実現する手法がいくつか提案されてきており、CPU速度とディスク速度の差が大きい現代では、非常に有効な高速化の方法となっています。

【参考文献】
[1] Justin Zobel, Alistair Moffat, Inverted files for text search engines, ACM Computing Surveys (CSUR), 2006
[2] Ian H. Witten, Alistair Moffat, Timothy C. Bell, Managing Gigabytes: Compressing and Indexing Documents and Images, Morgan Kaufmann Publisher, 1999
[3] C. D. Manning, P. Raghavan, H. Schutze, Introduction to Information Retrieval, Cambridge University Press, 2008
[4] M. Zukowski , S. Heman , N. Nes , P. Boncz, Super-Scalar RAM-CPU Cache Compression, Proceedings of the 22nd International Conference on Data Engineering, 2006
[5]H. Yan, S. Ding, T. Suel, Inverted index compression and query processing with optimized document ordering, , Proceeding of the 17th international conference on World Wide Web, 2009
[6] J. Zhang , X. Long , T. Suel, Performance of compressed inverted list caching in search engines, Proceeding of the 17th international conference on World Wide Web, 2008

おすすめ記事

記事・ニュース一覧